Densitet

Vi förklarar vad som är densiteten, dess formel, hur man beräknar den, de typer som finns och ger flera exempel

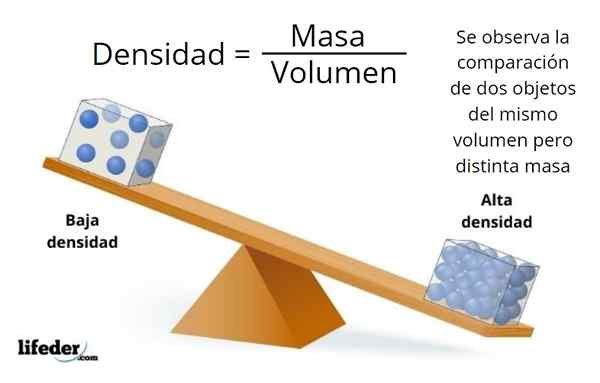
Mellan två föremål med lika volym är den med den största densiteten en som har den största massan

Vad är densitet?

De densitet av ett ämne av ett ämne är kvoten mellan provets massa och volymen den upptar, är dess måttenhet kg/m³ I det internationella enhetssystemet. Den grekiska bokstaven ρ (rho) används ofta för att beteckna det.

Vattentäthet, som är universell vätska, är 1000 kg/m³ o 1 g/cm³ vid 25 ºC, eftersom densiteten upplever förändras med temperatur och tryck.

Många gånger finns det föremål med samma dimensioner, och ändå är vissa lättare och tyngre, detta beror på densitetsskillnader. Det lättare objektet har mindre densitet än de tyngsta.

Densitet är en intensiv egenskap hos materia, som inte beror på mängden massa på provet som undersöks, eftersom det är massa/volymandelen som förblir konstant för samma substans. Detta tillåter att skilja ett ämne från en annan.

Materialen har ett brett utbud av tätheter, minderåriga är de för gaser, så enheten kg/m³ Det är mycket stort och gram/liter eller G/L är föredraget. Andra ofta använda enheter är gram/milliliter eller gram/kubikcentimeter.

Begreppet densitet är särskilt användbart när man arbetar med kontinuerliga medel som vätskor, vare sig gaser eller vätskor.

Täthetsformel

Enligt den givna definitionen har densiteten en matematisk formel som ges av:

Där densiteten är ρ, m är mass- och v -volymen.

Hur mäts densiteten?

Densiteten för ett objekt kan beräknas om dess massa och volym tidigare mäts. Det senare är inte alltid lätt, eftersom provet kan vara oregelbundet, men det finns flera metoder.

Kan tjäna dig: Mars (planet)

Geometrisk metod

Om provet har en regelbunden geometrisk form finns formler som tillåter beräkning av volymen baserat på dess dimensioner. När det gäller degen kan detta erhållas med hjälp av en balans.

Etableringsmetod: Volymförskjutning

Mätning av volymen av en nyckel med den fördrivna volymen

Om objektet inte är regelbundet kan dess volym bestämmas genom att mäta den fördrivna volymen när den är helt nedsänkt i en vätska som vatten.

För detta används en examen behållare och fylld med en exakt volym vatten v₁, Då är objektet helt nedsänkt och den nya volym V mäts₂. Objektets volym är lika med skillnaden v₂ - V₁.

För att använda denna metod bör provämnet inte lösas i vattnet och du måste ha en examen behållare med rätt storlek.

Densitet genom Archimedes -principen

Archimedes -principen kan användas för att ta reda på tätheten för ett fast prov. Principen säger att en partiell eller helt nedsänkt kropp genomgår en stigande kraft som kallas push, vars storlek är lika med vikten på den fördrivna vätskan vid placering av kroppen.

För att bestämma tätheten för ett objekt genom Archimedes -principen följs dessa steg:

• Steg 1

Bestäm massan m_c av objektet genom en balans.

• Steg 2

Fyll en behållare med en vätska vars densitet är känd, som vanligtvis destilleras vatten. Detta värde kallas m₁.

• Steg 3

Sänk helt det fasta objektet i behållaren med vatten och se till att jag inte rör vid väggarna. Det observeras att vätskan utövar en drivkraft OCH På det fasta upp, och detta i sin tur, med Newtons tredje lag, utövar en reaktion av lika stor storlek på vattnet, men i motsatt riktning.

Kan tjäna dig: Solid State Physics: Egenskaper, struktur, exempel

Att väga uppsättningen, det erhållna värdet, kallat m₂, Det kommer att vara behållaren full med vatten mer denna reaktion.

• Steg 4

Från ekvationen för densitet kan kroppens volym V uttryckas, vilket motsvarar volymen för förskjuten vätska:

Där m_c och ρ_c Kroppens massa och densitet är respektive medan M_F och ρ_c De är massa och densitet för den fördrivna vätskan. Från detta uttryck rensas tätheten på kroppen ρ_c:

Vätskans massa utkastade m_F Det är helt enkelt:

m_F = m₂ −M₁

Därför:

Typer av täthet

Absolut densitet  

Det är densiteten som tidigare definierats: kvoten mellan massan och provets volym.

Relativ densitet

Kallas också Specifik gravitation, Det är en täthet av ett ämne med avseende på en annan som tas som referens. För fasta ämnen och vätskor är detta referensämnet vatten vid 4 ° C och 1 atm tryck och för gaser är den torr luft. Det beräknas av:

Relativ densitet = Densitet för vatten/densitet av vatten

Både materialets densitet och vattnet måste mätas under identiska tryck och temperatur och uttrycka sig i samma enheter.

Följande bild visar de relativa tätheterna av stål och trä.

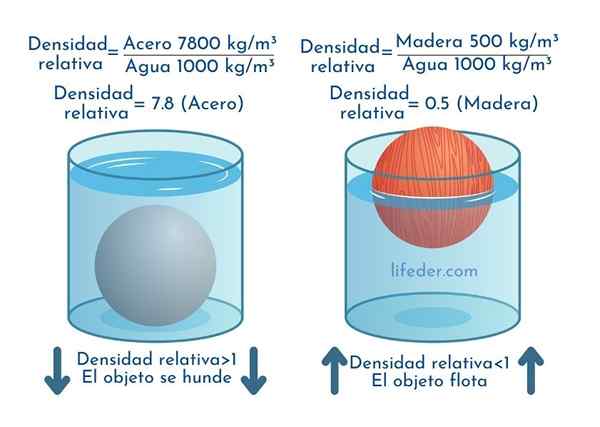
Eftersom ståltätheten är 7800 kg/m³ Och vattnet är 1000 kg/m³, Den relativa tätheten av stål, betecknad som SG, är:

SG = 7800 /1000 = 7.8

För sin del är träets relativa densitet:

SG = 500/1000 = 0.5

Föremål vars relativa densitet är mindre än 1 flyter i vattnet, medan de vars relativa densitet är större än 1 handfat.

Uppenbar densitet

Det beräknas av kvoten mellan provet och dess volym, inklusive porer och luftutrymmen:

Kan tjäna dig: slumpmässigt fel: formel och ekvationer, beräkning, exempel, övningar

Uppenbar densitet = massa / volym = (massa _partiklar + Massa _luft )/ (Volym _partiklar+ Volym _luft)

Täthetsexempel

• Den lättaste metallen av allt är litium, med 530 kg/m densitet³
• Blodtätheten är 1060 kg/m³
• Osmium är den mest kända metallen, med en densitet på 22570 kg/m³
• Kvarkplasma har en densitet av 1 × 10¹⁹ kg/m³

Löst övningar

Övning 1

Beräkna korkens densitet, veta att en kub gjord med detta material, som mäter 1.5 cm sida, har en massa på 1 g.

• Lösning

Volymen på en kub är:

V = ℓ³ = (1.5 cm)³ = 3.375 cm³

Uttalandet indikerar att massan m för kuben är m = 1 g, därför ersätter värden i densitetsekvationen:

ρ = m / v = 1g / 3.375 cm³ = 0.296 g/cm³

Övning 2

Vad är massan av en sfär gjord av 15 cm radio osmium?

• Lösning

Börjar från densitetsekvationen:

Degen rensas som:

M = ρ ∙ v

Det är nödvändigt att beräkna sfärens volym, som ges av formeln:

Att vara r sfärens radie. Eftersom osmiums densitet är 22570 kg/m³, Det är bekvämt att uttrycka 15 cm i meter:

R = 15 cm = 15 × 10⁻² m

V = (4/3) π × (15 × 10⁻² m)³ = 0.01414 m³

Detta värde ersätts i degen:

M = ρ ∙ V = 22570 kg/m³ × 0.01414 m³ = 319.1 kg

Referenser

1. Chang, R. 2013. Kemi. 11VA. Utgåva. McGraw Hill Education.
2. Giancoli, D.  2006. Fysik: Principer med applikationer. Sjätte. Ed Prentice Hall.
3. Shipman, J. 2009. En introduktion till fysisk vetenskap. Tolfte upplagan. Brooks/Cole, Cengage Editions.
4. Tippens, s. 2011. Fysik: koncept och applikationer. Sjunde upplagan. McGraw Hill.
5. University of Antioquia. Fasta ämnen. Återhämtat sig från: undervisning.du.Edu.co.