Algebraiska derivat

Vad är algebraiska derivat?

De algebraiska derivat De består av studien av derivatet i det specifika fallet med algebraiska funktioner. Ursprunget till begreppet derivat går tillbaka till antika Grekland. Utvecklingen av denna uppfattning motiverades av behovet av att lösa två viktiga problem, en i fysik och en i matematik.

I fysiken löser derivatet problemet med att bestämma den omedelbara hastigheten för ett rörligt objekt. I matematik tillåter det att hitta tangentlinjen till en kurva vid en given punkt.

Även om det verkligen finns många fler problem som löses genom att använda derivatet, såväl som dess generaliseringar, kom resultaten som kom senare till införandet av deras koncept.

Pionjärerna med differentiell kalkyl är Newton och Leibniz. Innan vi ger den formella definitionen kommer vi att utveckla idén bakom, från den matematiska och fysiska synvinkeln.

Derivatet som väntar på tangentlinjen till en kurva

Anta att grafen för en y = f (x) -funktion är en kontinuerlig graf (utan spikar eller hörn eller separationer), och antingen a = (a, f (a)) en fast punkt över den. Vi vill hitta tangentlinjekvationen till funktionen f vid punkt a.

Låt oss ta en annan punkt P = (x, f (x)) i grafen, nära punkt a, och spåra torklinjen som passerar genom en och p. En torklinje är en linje som skärs till diagrammet för en kurva i en eller flera punkter.

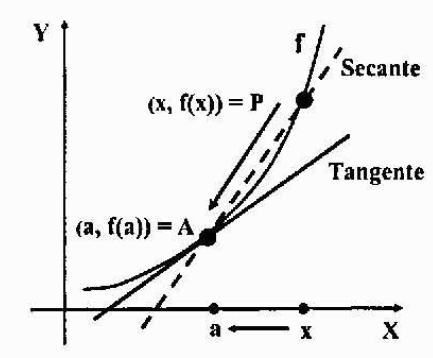
För att få den tangentlinjen som vi vill ha är det bara nödvändigt att beräkna lutningen eftersom vi redan har en punkt i linjen: punkten a.

Om vi ​​flyttar punkten P med grafen och vi närmar oss den mer och mer till punkt A, kommer den tidigare nämnda torra linjen att närma sig den tangentlinjen som du vill hitta. Med gränsen när "P tenderar till en" kommer båda linjerna att sammanfalla, därför kommer deras sluttningar också.

Secant -linjens lutning ges av

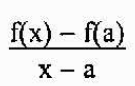
Att säga att P är nära A, motsvarar att säga att "X" närmar sig "A". Således kommer lutningen på tangentlinjen till grafen för F vid punkt A att vara lika med:

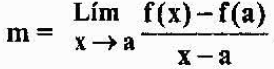
Det föregående uttrycket betecknas av f '(a) och definieras som derivat av en funktion f vid punkten "a". Vi ser att analytiskt är derivatet av en funktion vid en punkt en gräns, men geometriskt är det lutningen på linjen tangent till funktionsdiagrammet vid punkten.

Kan tjäna dig: slumpmässig variabel: koncept, typer, exempel

Nu kommer vi att se denna uppfattning ur fysikens synvinkel. Vi kommer att nå samma uttryck för den föregående gränsen, även om det är genom en annan väg, och därmed erhåller definitionen enhällighet.

Derivatet som omedelbar hastighet för ett rörligt objekt

Låt oss titta på ett kort exempel på vad omedelbar hastighet betyder. När det sägs till exempel att en bil för att nå en destination gjorde det med en hastighet på 100 km per timme, vad det betyder är att på en timme reste han 100 km.

Detta betyder inte nödvändigtvis att bilen alltid var 100 km under hela timmen, bilens vekimeter i vissa ögonblick skulle markera mindre eller mer. Om han hade behovet av att stå vid ett trafikljus var hastigheten i det ögonblicket 0 km. Men efter en timme var rutten 100 km.

Detta är vad som kallas medelhastighet och ges av kvoten på avståndet mellan den tid som förflutits, som vi just har sett. Den omedelbara hastigheten är under tiden den som markerar en bilens velocimeternål på ett visst ögonblick (tid).

Låt oss se detta nu mer allmänt sätt. Anta att ett objekt rör sig längs en linje och att denna förskjutning representeras med hjälp av ekvationen S = f (t), där variabeln t mäter tiden och variabeln S förskjutningen, med hänsyn till dess början i ögonblicket t = 0, då det också är noll, det vill säga F (0) = 0.

Denna funktion f (t) kallas positionsfunktion.

Ett uttryck för objektets omedelbara hastighet söks på ett fast ögonblick. I denna hastighet kommer vi att beteckna den med v (a).

Vare sig det är varje ögonblick nära omedelbart "A". I tidsintervallet mellan "A" och "T" ges positionens förändring av f (t) -f (a).

Medelhastigheten i detta tidsintervall är:

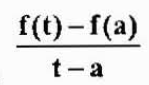
Vilket är en tillnärmning av omedelbar hastighet V (a). Detta tillvägagångssätt kommer att bli bättre när T kommer närmare "A". Därför,

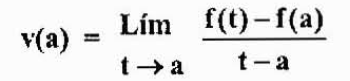
Låt oss märka att detta uttryck är lika med det som erhållits i föregående fall, men ur ett annat perspektiv. Detta är vad som kallas derivatet av en F -funktion vid en punkt "A" och betecknas av F '(A), som anges ovan.

Kan tjäna dig: exponenters lagar

Observera att göra förändringen h

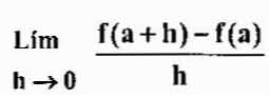
Båda uttryck är likvärdiga men ibland bör det användas mer till en istället för den andra, beroende på fallet.

Det definieras sedan mer generellt som härrör från en funktion f vid någon punkt "x" som tillhör dess domän som

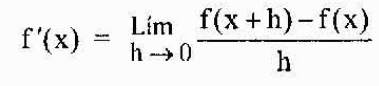
Den vanligaste notationen för att representera derivatet av en funktion y = f (x) är det vi just har sett (f 'o y'). En annan allmänt använt notation är emellertid notationen av Leibniz som representeras som något av följande uttryck:

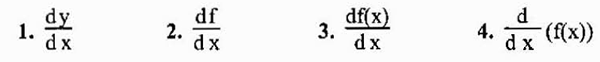
Med tanke på det faktum att derivatet i huvudsak är en gräns kan det eller inte existerar, eftersom gränserna inte alltid finns. Om det finns, sägs det att funktionen i fråga kan differentieras vid den givna punkten.

Algebraisk funktion

En algebraisk funktion är en kombination av polynom genom summor, subtraktioner, produkter, kvoter, krafter och radikaler.

Ett polynom är ett uttryck för form

P_n= a_nxⁿ+ till_N-1x^N-1+ till_N-2x^N-2+... + a₂x²+ till₁x+a₀

Där n är ett naturligt antal och alla_Yo, Med i = 0,1, ..., n är rationella siffror och_n≠ 0. I detta fall sägs det att graden av detta polynom är n.

Följande är exempel på algebraiska funktioner:

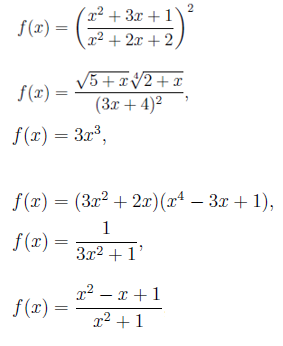
Här ingår inte de exponentiella, logaritmiska och trigonometriska funktionerna. Deriveringsreglerna som vi ser nedan är giltiga för funktioner i allmänhet, men vi kommer att begränsa och tillämpa dem vid algebraiska funktioner.

Derrying regler

Härledd från en konstant

Säger att derivatet av en konstant är noll. Det vill säga om f (x) = c, då f '(x) = 0. Till exempel är derivatet av konstant funktion 2 lika med 0.

Härledd från en kraft

Om f (x) = xⁿ, sedan f '(x) = nx^N-1. Till exempel x derivat³ Det är 3x². Som en följd av detta erhålls det att det härrörande från identitetsfunktionen f (x) = x är f '(x) = 1x^1-1= x⁰= 1.

Ett annat exempel är som följer: Låt f (x) = 1/x², sedan f (x) = x^-2 och f '(x) = -2x^-2-1= -2x^-3.

Den här egenskapen är också giltiga rötter, eftersom rötterna är rationella krafter och ovanstående kan också tillämpas i så fall. Till exempel ges de härrörande från en kvadratrot av

Det kan tjäna dig: uppskattning med intervall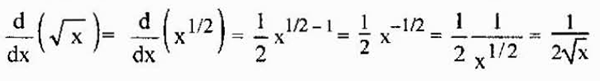

Härrörande från en summa och en subtraktion

Om f och g är differentierbara funktioner i x, är summan f+g också och det uppfylls att (f+g) '(x) = f' (x)+g '(x) (x) (x).

På liknande sätt måste du (f -g) '(x) = f' (x) -g '(x). Med andra ord, derivatet av en summa (subtraktion) är summan (eller subtraktionen) av derivaten.

Exempel

Om h (x) = x²+X-1, då

H '(x) = (x²)+(x) '-(1)' = 2x+1-0 = 2x+1.

Produkt härrörande från en produkt

Om f och g är differentierbara funktioner i x, är FG -produkten också differentierbar i x och det uppfylls det

(fg) '(x) = f' (x) g (x)+f (x) g '(x).

Som en konsekvens har den om C är en konstant och F är en differentierbar funktion i x, då är CF också differentierbar i x y (CF) '(x) = CF' (x).

Exempel

Om f (x) = 3x (x²+1), då

f '(x) = (3x)' (x²+1)+(3x) (x²+1) '= 3 (x)' (x²+1)+3x [(x²) '+(1)]

= 3 (1) (x²+1)+3x [(2x^2-1) +0] = 3 (x²+1)+3x (2x) = 3x²+3+6x²

= 9x²+3.

Härledd från en kvot

Om f och g är differentierbar i x och g (x) ≠ 0, är ​​f/g också differentierbar i x, och det uppfylls det

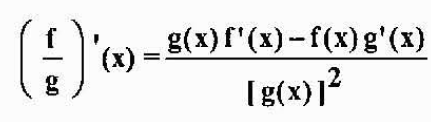
Exempel: Om h (x) = x³/(x²-5x), då

H '(x) = [(x³) '(X⁵-5x)-(x³) (x⁵-5x) ']/ (x⁵-5x)²= [(3x²) (x⁵-5x)- (x³) (5x⁴-5)]/ (x⁵-5x)².

Kedjeregel

Denna regel gör det möjligt att härleda funktionernas sammansättning. Den fastställer följande: om y = f (u) är differentierbar i u, och u = g (x) är differentierbar i x, är föreningsfunktionen f (g (x)) differentierbar i x, och det uppfylls det [f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f (f g (x))] '= f' (g (x)) g '(x).

Det vill säga derivatet av en sammansatt funktion är produkten från derivatet av den externa funktionen (externt derivat) med den interna funktionen härledd (internt derivat).

Exempel

Om f (x) = (x⁴-2x)³, så

f '(x) = 3 (x⁴-2x)²(x⁴-2x) '= 3 (x⁴-2x)²(4x³-2).

Det finns också resultat för att beräkna det konverserade derivatet av en funktion, liksom generaliseringen till derivat med högre ordning. Ansökningarna är omfattande. Bland dem markeras deras vinster i optimering och minimifunktioner.

Referenser

1. Alarcon, s., González, m., & Quintana, h. (2008). Differentiell kalkyl. DET M.
2. Cabrera, V. M. (1997). 4000 beräkning. Redaktionell progreso.
3. Castaño, h. F. (2005). Matematik före beräkningen. University of Medellin.
4. Eduardo, n. TILL. (2003). Introduktion till beräkning. Paraplyutgåvor.
5. Källor, a. (2016). Grundläggande matematik. En introduktion till beräkning. Lulu.com.
6. Purcell, E. J., Rigdon, s. OCH., & Varberg, D. OCH. (2007). Beräkning. Pearson Education.
7. Saenz, j. (2005). Differentiell kalkyl (Second ED.). Barquisimeto: Hypotenusa.
8. Thomas, g. B., & Weir, m. D. (2006). Beräkning: Flera variabler. Pearson Education.