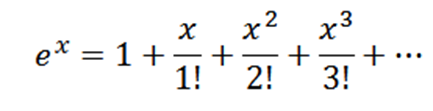På varandra följande derivat

Vad är successiva derivat?

De på varandra följande derivat De är de härrörande från en funktion efter det andra derivatet. Processen för att beräkna successiva derivat är som följer: det finns en funktion f, som vi kan härleda och erhålla den härledda funktionen f '. Till detta derivat av f kan vi härleda det igen, erhålla (f ')'.

Denna nya funktion kallas andra derivat; Alla derivat beräknade från det andra är på varandra följande; Dessa, även kallade en högre ordning, har stora applikationer, som att ge information om slaget i grafen för en funktion, testet av det andra derivatet för relativa ändar och bestämning av oändliga serier.

Definition

Med hjälp av leibniz -notation har vi att derivatet av en "y" -funktion med avseende på "x" är dy/dx. För att uttrycka till det andra derivatet av "y" med hjälp av notationen av Leibniz, skriver vi enligt följande:

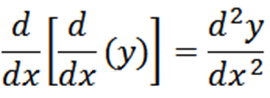
I allmänhet kan vi uttrycka successiva derivat enligt följande med notationen av Leibniz, där N representerar derivatets ordning.

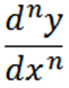
Andra notationer som används är följande:

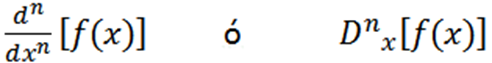
Några exempel där vi kan se de olika notationerna är:

Exempel 1

Få alla derivat av F -funktionen definierade av:

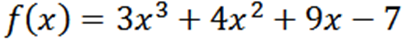
Med hjälp av de vanliga remissteknikerna har vi att F är:

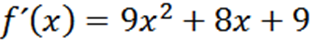
Upprepa processen kan vi få det andra derivatet, det tredje derivatet och så vidare.

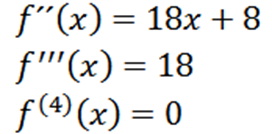
Observera att det fjärde derivatet är noll och nollderivatet är noll, så vi måste:

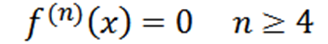
Exempel 2

Beräkna den fjärde härledda från följande funktion:

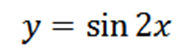
Erhålla den givna funktionen vi har som ett resultat:

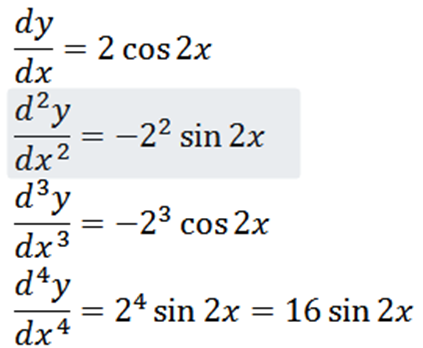
Hastighet och acceleration

En av motivationerna som ledde till upptäckten av derivatet var sökningen efter definitionen av omedelbar hastighet. Den formella definitionen är som följer:

Kan tjäna dig: Primo -nummer: Egenskaper, exempel, övningar

Låt y = f (t) en funktion vars graf beskriver banan för en partikel på ett ögonblick t, Sedan ges hans hastighet på ett ögonblick av::

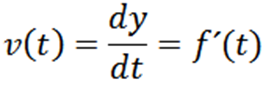
När hastigheten på en partikel har erhållits kan vi beräkna omedelbar acceleration, som definieras enligt följande:

Den omedelbara accelerationen av en partikel vars bana ges av y = f (t) är:

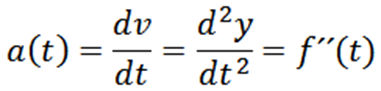
Exempel 1

En partikel rör sig på en linje enligt positionsfunktionen:

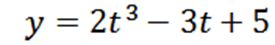
Där "y" mäts i meter och "t" på några sekunder.

• I vilket ögonblick är din hastighet 0?
• I vilket ögonblick är accelerationen 0?

Genom att härleda "Y" -positionfunktionen har vi att dess hastighet och acceleration ges respektive av:

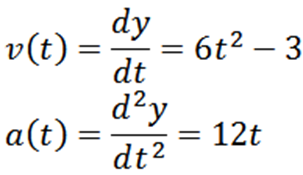
För att besvara den första frågan räcker det för att avgöra när V -funktionen V är noll; detta är:

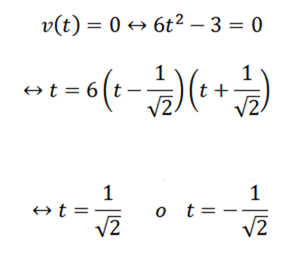
Vi fortsätter med nästa fråga analog:

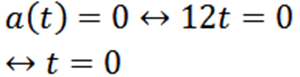
Exempel 2

En partikel rör sig på en linje enligt följande rörelsekvation:

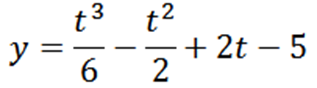
Bestäm "T, Y" och "V" när A = 0.

Att veta att hastighet och acceleration ges av

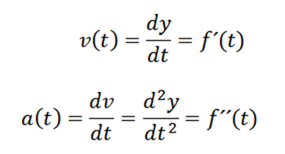
Vi fortsätter att härleda och få:

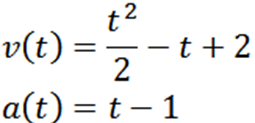
Gör a = 0, vi har:

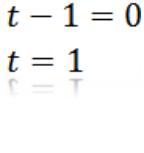
Där vi kan dra slutsatsen att värdet på t så att A är lika med noll är t = 1.

Sedan, utvärdera i t = 1 positionen och funktionsfunktionen, måste vi:

Ansökningar

Mplícita -härledning

På varandra följande derivat kan också erhållas genom implicit härledning.

Exempel

Med tanke på följande ellips, hitta "Y":

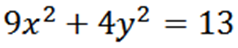
Implicit härstammar med avseende på X, vi har:

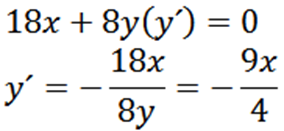
Sedan, återförsäljande implicit med avseende på X, ger oss:

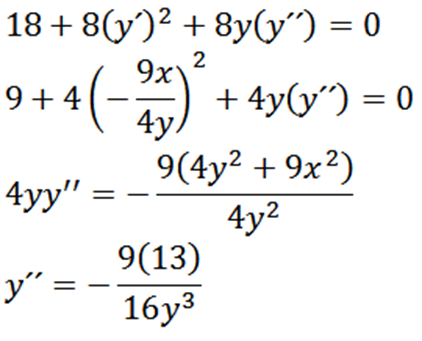
Slutligen har vi:

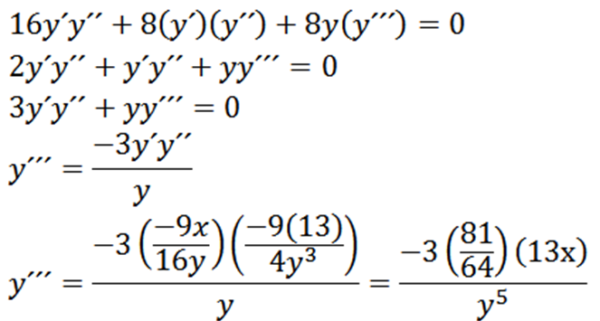
Relativa ytterligheter

En annan användning som vi kan ge till andra beställningsderivat är i beräkningen av relativa ändar av en funktion.

Kan tjäna dig: hur många symmetrixlar har en cirkel?

Kriterierna för det första derivatet för lokala ytterligheter säger att om vi har en kontinuerlig F -funktion i ett intervall (a, b) och det finns en c som tillhör nämnda intervall så att det upphävs i c (det vill säga att c är en kritisk punkt), ett av dessa tre fall kan inträffa:

• Om f '(x)> 0 för alla x som tillhör (a, c) och f' (x)<0 para x perteneciente a (c,b), entonces f(c) es un máximo local.
• Om f '(x) 0 för x som tillhör (c, b), är f (c) ett lokalt minimum.
• Om f '(x) har samma inloggning (a, c) och i (c, b), innebär det att f (c) inte är ett lokalt slut.

Med hjälp av kriterierna för det andra derivatet kan vi veta om ett kritiskt antal funktion är ett maximalt eller ett lokalt minimum, utan att behöva göra vad som är tecknet på funktionen med ovannämnda intervall.

Kriteriet för den andra driften säger att om f '(c) = 0 och att f "(x) är kontinuerlig i (a, b), händer det om f" (c)> 0 då f (c) är en Lokalt minimum och om f "(c) < 0 entonces f(c) es un máximo local.

Om f "(c) = 0 kan vi inte dra slutsatsen någonting.

Exempel

Med tanke på funktionen f (x) = x⁴ + (4/3) x³ - 4x², Hitta den maximala och minsta släktingen för att tillämpa kriterierna för det andra derivatet.

Först beräknar vi f '(x) och f "(x) och vi har:

f '(x) = 4x³ + 4x² - 8x

f "(x) = 12x² + 8x - 8

Nu, f '(x) = 0 ja, och bara om 4x (x + 2) (x - 1) = 0, och detta inträffar när x = 0, x = 1 eller x = - 2.

För att bestämma om de erhållna kritiska siffrorna är relativa ytterligheter utvärderar bara i F "och därmed observera dess tecken.

Kan tjäna dig: Hepagon

f "(0) = - 8, så f (0) är ett lokalt maximum.

f "(1) = 12, så f (1) är ett lokalt minimum.

f "(- 2) = 24, så f (- 2) är ett lokalt minimum.

Taylor Series

Vara f en funktion definierad på följande sätt:

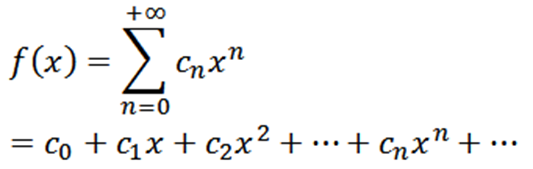
Denna funktion har en radie av konvergens r> 0 och har härrör från alla beställningar i (-r, r). På varandra följande derivat av f Ge oss:

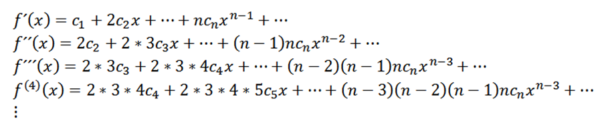
Med x = 0 kan vi få värdena på c_n beroende på dess derivat enligt följande:

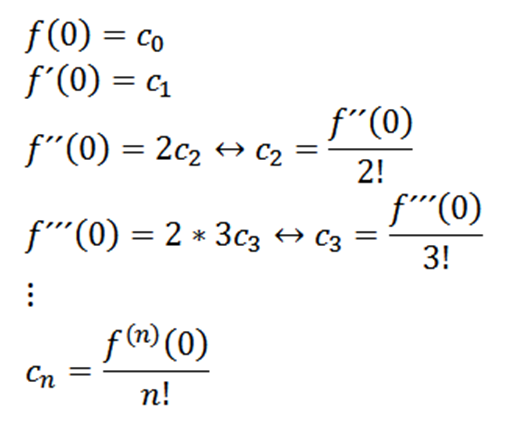
Om vi ​​tar n = 0 som funktionen f (dvs. f^0 = f), kan vi skriva om funktionen enligt följande:

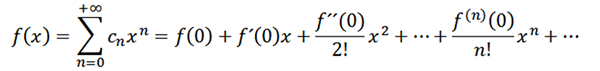
Låt oss nu betrakta funktionen som en serie krafter vid x = a:

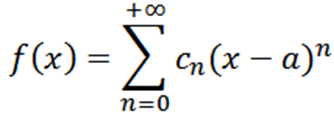
Om vi ​​utför en analys som är analog med den föregående, skulle vi behöva skriva funktionen f som:

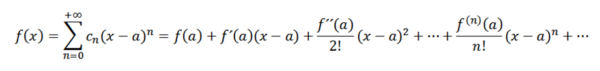
Dessa serier är kända som Taylor F i en serie. När A = 0 har vi det specifika fallet som heter MacLaurin -serien. Denna typ av serie är av stor matematisk betydelse, särskilt i numerisk analys, eftersom tack vare dessa kan vi definiera funktioner i datorer som E^x , Sin (x) och cos (x).

Exempel

Skaffa MacLaurin -serien för E^x.

Observera att om f (x) = e^x, sedan f^(N)(x) = e^x och f^(N)(0) = 1, så din maclaurin -serie är: