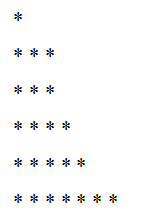Tillsatsnedbrytning

De tillsatsnedbrytning av ett positivt heltal är att uttrycka det som en summa av två eller flera positiva siffror. Således har vi att nummer 5 kan uttrycka det som 5 = 1+4, 5 = 2+3 eller 5 = 1+2+2. Var och en av dessa sätt att skriva nummer 5 är vad vi kommer att kalla tillsatsnedbrytning.

Om vi ​​uppmärksammar kan vi se att uttryck 5 = 2+3 och 5 = 3+2 representerar samma sammansättning; Båda har samma siffror. Emellertid skrivs endast för en fråga om komfort vanligtvis var och en av annonserna efter kriterierna från minst till största.

Tillsatsnedbrytning

Som ett annat exempel kan vi ta nummer 27, vilket vi kan uttrycka det som:

27 = 7+10+10

27 = 9+9+9

27 = 3+6+9+9

27 = 9+18

Tillsatsnedbrytning är ett mycket användbart verktyg som gör att vi kan stärka vår kunskap om numreringssystem.

Kanonisk tillsatsnedbrytning

När vi har antal på mer än två siffror är en viss form av att sönderdela dem i multiplarna 10, 100, 1000, 10 000, etc., som utgör det. Detta sätt att skriva valfritt nummer kallas kanonisk tillsatsnedbrytning. Till exempel kan nummer 1456 sönderdelas på följande sätt:

1456 = 1000 + 400+ 50 + 6

Om vi ​​har nummer 20 846 295 kommer din kanoniska tillsatsnedbrytning att vara:

20 846 295 = 20 000 000 + 800 000 + 40 000 + 6000 + 200 + 90 +5.

Tack vare denna nedbrytning kan vi se att värdet på en given siffra ges av den position den upptar. Låt oss som ett exempel siffrorna 24 och 42:

24 = 20 + 4

42 = 40 +2

Här kan vi se att i 24 har de 2 ett värde på 20 enheter och på 4 ett värde på 4 enheter; Å andra sidan har 42 42 ett värde på 40 enheter och de två av två enheter. Även om båda siffrorna använder samma siffror är deras värden helt olika utifrån den position de upptar.

Kan tjäna dig: x kvadrat

Ansökningar

En av de applikationer som vi kan ge till tillsatsnedbrytning är i vissa typer av demonstrationer, där det är mycket användbart att se ett positivt heltal som summan av andra.

Exempel på teorem

Låt oss som ett exempel följande teorem med deras respektive demonstrationer.

- Vara z ett helt antal 4 siffror, då är z delbar med 5 om dess siffra motsvarande enheterna är noll eller fem.

Demonstration

Låt oss komma ihåg vad som är delbarhet. Om vi ​​har "A" och "B" hela siffror, säger vi att "A" Divides "B" om det finns ett heltal "C" så att B = A*C.

En av egenskaperna för delbarhet säger att om "A" och "B" är delbara mellan "C", så är subtraktionen "A-B" också.

Vara z ett helt antal fyra siffror; Därför kan vi skriva till Z och Z = ABCD.

Med hjälp av kanonisk tillsatsnedbrytning måste vi:

Z = A*1000 + B*100 + C*10 + D

Det är uppenbart att A*1000 + B*100 + C*10 är delbar mellan 5. Det är därför vi har att z är delbar mellan 5 om z - (a*1000 + b*100 + c*10) är delbar mellan 5.

Men z - (a*1000 + b*100 + c*10) = d och d är ett enda figurnummer, så det enda sättet att vara delbart mellan 5 är att det är 0 eller 5.

Därför är z delbar mellan 5 om d = 0 eller d = 5.

Observera att om Z har N -siffror demonstrationen är exakt densamma ändrar det bara att vi nu skulle skriva z = a₁TILL₂Till ... till_n Och målet skulle vara att bevisa det_n är noll eller fem.

Partitioner

Vi säger att en partition av ett positivt heltal är ett sätt på vilket vi kan skriva ett nummer som en summa av positiva heltal.

Kan tjäna dig: konvergensradio: definition, exempel och övningar löst

Skillnaden mellan en tillsatsnedbrytning och en partition är att, medan den i den första söks att den åtminstone kan delas upp i två eller flera, i partitionen denna begränsning.

Således har vi följande:

5 = 5

5 = 1+4

5 = 2+3

5 = 1+2+2

Ovanstående är partitioner av 5.

Det vill säga vi har att all tillsatsnedbrytning är en partition, men inte all partition är nödvändigtvis en tillsatsnedbrytning.

I siffror teori garanterar den grundläggande teoremet för aritmetiska att varje helt nummer kan skrivas unikt som en produkt av kusiner.

När partitionerna studeras är målet att avgöra hur många sätt ett positivt heltal kan skrivas som summan av andra heltal. Därför definierar vi partitionsfunktionen som presenteras nedan.

Definition

Partition P (n) -funktion definieras som antalet sätt på vilket ett positivt heltal n kan skrivas som en summa av positiva heltal.

När vi återvänder till exemplet 5 måste vi:

5 = 5

5 = 1+4

5 = 2+3

5 = 1+1+3

5 = 1+2+2

5 = 1+1+1+2

5 = 1+1+1+1+1

På detta sätt P (5) = 7.

Grafer

Både partitioner och tillsatsnedbrytningar av ett antal N kan representeras geometriskt.  Anta att vi har en tillsatsnedbrytning av N. I denna nedbrytning kan tillägget fixas så att medlemmarna i summan beställs från minst till största. Så det är värt:

n = a₁ + till₂ + till₃ +... + a_r med

till₁ ≤ a₂ ≤ a₃ ≤ ... ≤ a_r.

Vi kan grafera nämnda nedbrytning på följande sätt: I en första rad markerar vi a₁-Poäng, sedan i det följande markerar vi₂-poäng, och så vidare tills de når_r.

Kan tjäna dig: ojämlikheten i triangeln: demonstration, exempel, lösta övningar

Låt oss ta som exempel nummer 23 och dess nästa nedbrytning:

23 = 5 + 4 + 7 + 3 + 1 +3

Vi beställer denna sönderdelning och vi har:

23 = 1 + 3 + 3 + 4+ 5 + 7

Motsvarande graf skulle vara:

På samma sätt, om vi läser denna graf vertikalt istället horisontellt, kan vi få en nedbrytning som kanske skiljer sig från föregående. I exemplet med 23 sticker följande ut:

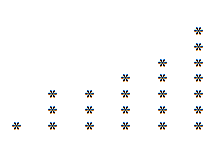
Så vi har de 23 vi kan också skriva det som:

23 = 6 + 5 + 5 + 3 + 2 + 1 + 1.