Ytutvidgningsformel, koefficienter och exempel

De ytlig utvidgning Det är utvidgningen som inträffar när ett objekt upplever variationer av ytan på grund av temperaturvariation. Det beror på materialets egenskaper eller dess geometriska form. Dilatation dominerar i två dimensioner i samma andel.

Till exempel i ett ark, när det finns en variation av temperaturen, är det ytan på densamma som lider av den största förändringen på grund av termisk utvidgning.

Ytan på en metallplatta som vanligtvis ses på gatorna. Källa: Pixabay.

Metallplåten i den föregående figuren ökar dess breda och dess längd märkbar när den värms upp av solstrålning. Tvärtom, båda minskar avsevärt när de kyls på grund av en minskning av omgivningstemperaturen.

Det är av denna anledning att när plattor är installerade på en våning, bör vissa kanter med andra inte träffas, men det måste finnas ett separationsutrymme som kallas dilatationskort.

Dessutom är detta utrymme fyllt med en speciell blandning som har en viss grad av flexibilitet, vilket förhindrar att brickor spricker på grund av starka tryck som termisk utvidgning kan producera.

[TOC]

Vad är ytlig utvidgning?

I ett fast material upprätthåller atomer sina mer eller mindre fasta relativa positioner runt en balanspunkt. På grund av termisk omrörning oscillerar de emellertid alltid runt den.

Genom att öka temperaturen ökar också termisk svängning, vilket gör att medelstora svängningspositioner förändras. Detta beror på att länkpotentialen inte är exakt parabolisk och har asymmetri runt det minsta.

Nedan är en siffra som beskriver den kemiska bindningsenergin beroende på det interatomiska avståndet. Den totala svängningsenergin vid två temperaturer visas också och hur svängningscentret rör sig.

Det kan tjäna dig: Pascal Tonel: Hur det fungerar och experiment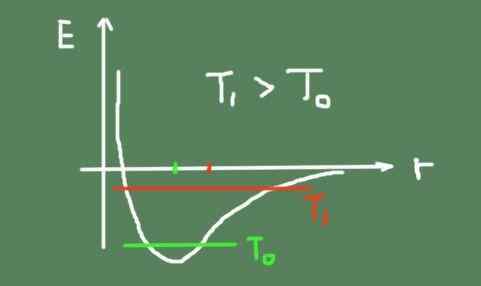Länk energidiagram kontra interatomiskt avstånd. Källa: Självgjord.

Ytlig utvidgning och dess koefficient

För att mäta den ytliga utvidgningen börjar vi från ett initialt område A och en initial temperatur T, av objektet som utvidgningen ska mätas.

Anta att detta objekt är en lamina i området A, och tjockleken på det är mycket lägre än kvadratroten i området a. Arket utsätts för en ΔT -temperaturvariation, så att den slutliga temperaturen på samma när den termiska balansen med värmekällan kommer att fastställas kommer att vara T '= T+ ΔT.

Under denna termiska process kommer ytan också att ha ändrats till ett nytt värde på '= A + ΔA. Således definieras ytdilationskoefficienten σ som förhållandet mellan den relativa variationen i arean per temperaturvariation.

Följande formel definierar den ytliga utvidgningskoefficienten σ:

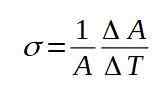
Den ytliga utvidgningskoefficienten σ är praktiskt taget konstant för ett brett spektrum av temperaturvärden.

På grund av definitionen av σ är dess dimensioner omvänd temperatur. Som en enhet används den vanligtvis ° C^-1.

Ytdilationskoefficient för olika material

Därefter ger vi en lista över den ytliga dilationskoefficienten för vissa material och element. Koefficienten beräknas i normalt atmosfärstryck baserat på en omgivningstemperatur på 25 ° C, och dess värde anses konstant i ett intervall av ΔT från -10 ° C till 100 ° C.

Enheten för den ytliga dilationskoefficienten kommer att vara (° C)^-1

- Stål: σ = 24 ∙ 10^-6 (° C)^-1

- Aluminium: σ = 46 ∙ 10^-6 (° C)^-1

Det kan tjäna dig: Magnetisering: Orbital och snurrmagnetiskt ögonblick, exempel

- Guld: σ = 28 ∙ 10^-6 (° C)^-1

- Koppar: σ = 34 ∙ 10^-6 (° C)^-1

- Mässing: σ = 36 ∙ 10^-6 (° C)^-1

- Järn: σ = 24 ∙ 10^-6 (° C)^-1

- Glas: σ = (14 till 18) ∙ 10^-6 (° C)^-1

- Kvarts: σ = 0,8 ∙ 10^-6 (° C)^-1

- Diamant: σ = 2 ,, 4 ∙ 10^-6 (° C)^-1

- Bly: σ = 60 ∙ 10^-6 (° C)^-1

- Ekved: σ = 108 ∙ 10^-6 (° C)^-1

- PVC: σ = 104 ∙ 10^-6 (° C)^-1

- Kolfiber: σ = -1,6 ∙ 10^-6 (° C)^-1

- Betong: σ = (16 till 24) ∙ 10^-6 (° C)^-1

De flesta material sträcker sig med en temperaturökning. Vissa material som kolfiber uppfyller emellertid temperaturökningen.

Löst exempel på ytlig utvidgning

Exempel 1

En stålplatta har dimensioner på 3 m x 5 m. På morgonen och i skuggan är temperaturen 14 ° C, men vid middagstid värmer den upp till 52 ° C. Hitta det sista området på plattan.

Lösning

Vi börjar från definitionen av ytlig dilationskoefficient:

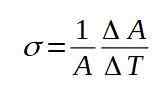
Härifrån rensar vi variationen i området:

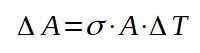
Vi fortsätter sedan att ersätta respektive värden för att hitta ökningen i området med temperaturökningen.

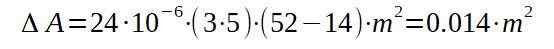
Det vill säga det slutliga området kommer att vara 15 014 kvadratmeter.

Exempel 2

Visa att den ytliga utvidgningskoefficienten är ungefär dubbelt så stor som den linjära dilationskoefficienten.

Lösning

Anta att vi börjar från en rektangulär platta med bredddimensioner LX och Long Ly, då kommer dess ursprungliga område att vara en = lx ∙ ly

Kan tjäna dig: termometriska skalor

När plattan lider av en temperaturökning ΔT, ökar dess dimensioner också att den nya bredd lx 'och dess nya ly', så att dess nya område kommer att vara en '= lx' ∙ ly '

Variationen som plattområdet lidit på grund av temperaturförändring kommer då att vara

ΔA = lx '∙ ly' - lx ∙ ly

där lx '= lx (1 + α Δt) och ly' = ly (1 + α Δt)

Det vill säga att förändringen av arean beroende på den linjära dilationskoefficienten och temperaturförändringen kommer att vara:

ΔA = Lx (1 + α ΔT) ∙ ly (1 + α ΔT) - Lx ∙ ly

Detta kan skrivas om som:

ΔA = lx ∙ ly ∙ (1 + α ΔT) ² - lx ∙ ly

Utveckla torget och multiplicera vi har följande:

Jag

Eftersom a är i storleksordningen 10^-6, Genom att höja det är det i storleksordningen 10^-12. Således är den kvadratiska termen i det föregående uttrycket föraktligt.

Då kan områdesökningen närmar sig av:

ΔA ≈ 2a ΔT lx ∙ ly

Men ökningen i området beroende på den ytliga dilationskoefficienten är:

ΔA = y ΔT a

Från där ett uttryck härleds som relaterar den linjära dilationskoefficienten till den ytliga dilationskoefficienten.

y ≈ 2 ∙ α

Referenser

1. Bauer, w. 2011. Fysik för teknik och vetenskap. Volym 1. Mac Graw Hill. 422-527
2. Giancoli, D. 2006. Fysik: Principer med applikationer. Sjätte. Utgåva. Prentice hall. 238-249.