120 delare

De 120 delare De är alla de siffror som delar det exakt. Dessa siffror är följande:

Delare av 120 = 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 30, 40, 60, 120

Också motsatserna till denna uppsättning siffror, det vill säga negativerna, är 120 delare, eftersom divisionen är exakt. 120 har 16 positiva hela delare och många andra negativa.

Det finns flera sätt att hitta delarna av ett nummer. Om detta inte är så stort kan du använda multiplikationstabellerna (för siffror mindre än 100) och verifiera i vilka tabeller som det aktuella antalet visas. Till exempel visas 12 i tabellerna 2, 3, 4 och 6, och dessa är deras delare, tillsammans med 1 och samma 12.

Antalet kan också delas upp i dess främsta faktorer, tillämpa uppdelningsreglerna och multiplicera faktorerna. Men du måste vara försiktig så att du inte passerar någon delare förbises.

Eftersom 120 är större än 100 är det inte direkt i multiplikationstabellerna, men det är inte för mödosamt att hitta sina 16. En giltig procedur för alla siffror visas omedelbart genom att använda mycket enkla tabeller.

Hur många delare är 120?

För det första är antalet delare av 120 att få reda på det. Det finns en formel som gör att du kan veta hur många du har, även om den inte säger vad de är.

Kompositnummer, såsom 120, kan uttryckas som produkten av primtal eller krafter hos dessa. Ring n till något sammansatt nummer:

N = aⁿ ∙ B^m ∙ C^p ... r^k

Kan tjäna dig: proportionalitetsrelationer: koncept, exempel och övningar

Siffrorna a, b, c ... r är primtal och värdena på n, m, p, ... k, respektive krafter. Nedbrytningen i främsta faktorer på 120 är som följer:

120 | 2
60 | 2
30 | 2
15 | 3
5 | 5
1 | 1

På detta sätt är 120 produkten av faktorerna:

120 = 2³ ∙ 3 ∙ 5

Formel för att beräkna antalet delare av N

Antal delare = (n +1) × (m +1) × (p +1) ... × (k +1)

Nu tillämpas formeln till 120. Från nedbrytning i faktorer måste du:

n = 3 (är kraften på 2)

M = 1 (3 är upphöjd till 1: 3¹ = 3)

P = 1 (de 5 verkar också förhöjda till 1)

Med dessa värden:

Antal delare på 120 = (3 +1) × (1 +1) × (1 +1) = 4 × 2 × 2 = 16

Detta resultat sammanfaller med början av början: 120 har 16 delare. Dessutom är det redan känt att 2, 3 och 5 är delare av 120, såväl som 10, eftersom valfritt antal i 0 är delbart med 10. Förfarandet för att hitta dem alla visas omedelbart.

Beräkning av delarna av 120

Det görs med hjälp av de faktorer som beräknas i föregående avsnitt. Där såg man att 2 är en främsta faktor med exponent 3, och 3 är en annan kusinfaktor, med exponent 1. Med denna information är följande tabell byggd:

Observera att krafterna på 2 börjar i 2⁰ och slut i 2³, vilket är den faktor som uppstår när man sönderdelas 120. Kom ihåg att 2⁰ och 3⁰ Båda är lika med 1 (valfritt antal höga till 0 är 1). För faktor 3 börjar det i 3⁰ Fram till 3¹, sedan 3¹ = 3.

Därefter är tabellen klar med produkten av siffrorna i rött, som visas här:

Kan tjäna dig: Multiplicative Inverse: Förklaring, exempel, lösta övningar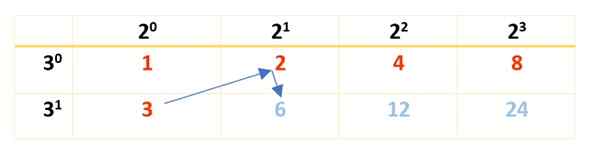

Alla röda och blå siffror är 120 delare, men det finns knappt 8. För att hitta de återstående, är ett nytt bord burst, de delare som redan har erhållits i första raden och den faktor som återstår att beaktas skrivs: 5, med sina krafter i den första kolumnen, till vänster, så här:

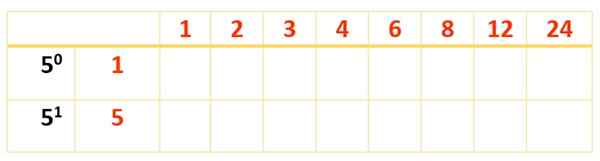
Nu är tabellen klar med produkterna från siffrorna i rött, vilket gjordes med den första tabellen:

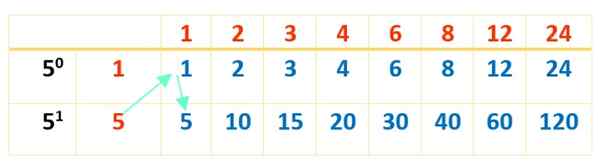
Och slutligen visas de 16 delarna på 120 i blått. Tabellerna är en utmärkt hjälp för operationer som ska göras i ordning och därmed nr 120 Divisor.

Löst övningar

Förfarandet för att hitta alla delare av ett nummer sammanfattas enligt följande:

1. Dela upp numret i främsta faktorer.
2. Beräkna antalet delare med formeln.
3. Bygg de nödvändiga tabellerna för att hitta delare. Om antalet har två faktorer räcker en tabell, om du har tre faktorer måste två tabeller göras, som i fallet med 120.

Övning 1

Hitta alla delare av 288.

Lösning

288 sönderdelas till främsta faktorer:

288 | 2
144 | 2
72 | 2
36 | 2
18 | 2
9 | 3
3 | 3
1 | 1

288 är skriven så här:

288 = 2⁵ ∙ 3²

Omedelbart är antalet delare på 288 till:

Antal delare = (n +1) × (m +1) × (p +1) ... × (k +1)

Från nedbrytningen i främsta faktorer noteras att n = 5 och m = 2, sedan:

Divisorer på 288 = (5 +1) × (2 +1) = 6 × 3 = 18

Det finns 18 delare och eftersom det bara finns två faktorer är det tillräckligt med bara en tabell:

Kan tjäna dig: egenskaper hos rektangeln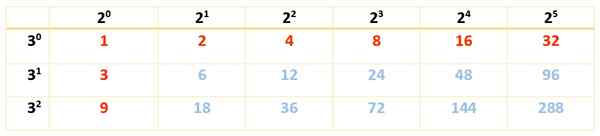

Delarna på 288 är siffrorna i rött och i blått:

Div (288) = 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 32, 36, 48, 72, 96, 144, 288

De kan snabbt kontrolleras med hjälp av en räknare.

Övning 2

Hitta delarna 350

Lösning

350 sönderdelas:

350 | 2
175 | 5
35 | 5
7 | 7
1 | 1

350 kan skrivas som en produkt av tre faktorer:

350 = 2 ∙ 5²∙ 7

Nästa steg är att beräkna hur många delare som har, genom formeln:

Antal delare = (n +1) × (m +1) × (p +1) ... × (k +1)

Med n = 1, m = 2, p = 1

Divisorer på 288 = (1 +1) × (2 +1) × (1 +1) = 2 × 3 × 2 = 12

Eftersom 350 kräver tre faktorer måste två tabeller göras. Den första görs med 2 och 5², Men det kan också göras med 2 och 7, eller med 7 och 5², Enligt preferensen, eftersom det slutliga resultatet i alla former är detsamma:

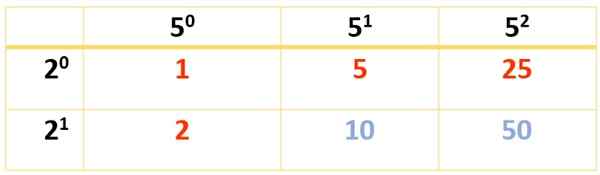
6 delare erhålls. De andra dyker upp med hjälp av denna andra tabell:

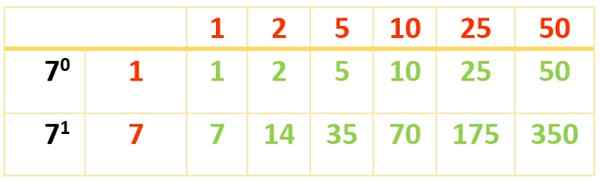
Delarna av 350 är:

Div (350) = 1, 2, 5, 7, 10, 14, 25, 35, 50, 70, 175, 350