Arrhenius ekvation

Vad är Arrhenius -ekvationen?

De Arrhenius ekvation Det är ett tillvägagångssätt som relaterar hastighetskonstanten för en kemisk reaktion beroende på temperatur. Det grundades 1899 av den svenska kemisten Svante Arrhenius (1859-1927). Representerar ett av de mest grundläggande bidragen i utvecklingen av kemisk kinetik.

Denna ekvation är skyldig sina teoretiska baser till många forskare, inklusive Wihelmy (1850), Berthelot (1862) och J. J. Hood (1885). Men det största inflytandet tillskrivs skapandet av Arrhenius -ekvationen till det arbete som gjorts av Van't Hoof (1884), som etablerade ett beroende av jämviktskonstanterna för de kemiska reaktionerna med temperaturen.

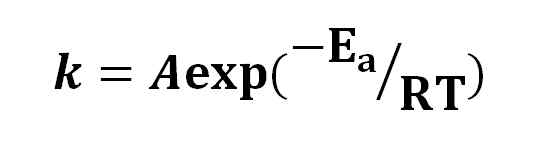Arrhenius ekvation. Källa: Gabriel Bolívar.

Baserat på Arrhenius -ekvationen har idén att en ökning med 10 ºC har orsakat en dubblering av reaktionshastigheten har spridits. Andra tolkningar som blir det är att molekyler behöver viss aktiveringsenergi för att reagera på varandra.

På samma sätt påpekas det att Arrhenius -ekvationen är en annan form av exponentiell sönderdelning där värdet på hastighetskonstanten beroende på exponenten -e_till/Rt, där e_till är aktiveringsenergi.

Ekvation och förklaring

Arrhenius -ekvationen har följande två uttryck:

K = ae^-Ea/rt

Form av ekvationen som används i kemi och är relaterad till reagensmullvad.

K = ae^-Ea/kbt

Form av ekvationen som används i fysiken och är relaterad till de fler molekylerna än med mullvad.

Båda härstammar från skåpbilens hovekvation för variationen i jämviktskonstanten K beroende på temperaturen. Basekvationen är:

d (ln k)/dt = e_till/Rt²

Det kan tjäna dig: Dibenzalacetona: egenskaper, reaktionsmekanism, användningar, risker

Vilket är integrerat förutsatt att_till är oberoende av temperaturen. Så vi har:

ln k = - e_till/Rt + ln a

Där ln a är integrationskonstanten. När den exponentiella funktionen appliceras på båda sidor av ekvationen får vi Arrhenius -ekvationen som redan introducerats.

Komponenter

k

Det är hastighetskonstanten för en kemisk reaktion. Dess värde kan erhållas, utöver användningen av Arrhenius -ekvationen, genom tillämpningen av hastighetslagen. Representerar antalet kollisioner mellan partiklar som produceras genom en reaktion per sekund.

TILL

Det är den så kallade pre-exponentiella faktorn, som representerar frekvensen av kollisioner mellan reagensmolekyler med en lämplig geometrisk orientering som kanske eller inte kan ge en kemisk reaktion. Om temperaturvariationen är av liten storlek tas den vanligtvis som konstant. Denna faktor har sin egen formel:

A = z ρ

Där z är känd som en frekvens- eller kollisionsfaktor, och ρ den geometriska eller steriska faktorn som indikerar molekylernas relativa orientering vid kollisionspunkten. Konstanten A har samma enheter som hastighetskonstanten. I det fall att det inte finns någon aktiveringsenergi kommer storleken på en att vara lika med K.

OCH_till

Det är aktiveringsenergin, som representerar tröskelenergin innan man når övergångsstaten.

Aktiveringsenergi har KJ/Mol -enheten. Men i beräkningarna används J/mol som en enhet. Det minsta (-) tecknet som föregår e_till, Det tjänar till att indikera att dess ökning ger en minskning av reaktionshastigheten, liksom dess minskning ger en ökning av reaktionshastigheten.

Kan tjäna dig: gaskromatografi

Rt

Representerar den genomsnittliga kinetiska energin. Samtidigt är R den universella konstanten av gaser, som är en av dess mest använda värden 8.31 J · K^-1· Mol^-1. Och T är den absoluta temperaturen som uttrycks i Kelvin (K).

och

Det är grunden för naturliga eller neperiska logaritmer, med ett värde på 2.71828.

och^-Ea/rt

Det är fraktionen av reagerande molekyler med lika eller överflödig energi i förhållande till aktiveringsenergi.

Ansökningar

De flesta tillämpningarna av Arrhenius -ekvationen kommer från användning för att bestämma hastighetskonstanten; och i förlängningen reaktionens hastighet såväl som dess aktiveringsenergi.

Till exempel har en kemisk modell utvecklats baserat på Arrhenius -ekvationen, som kan förutsäga materialsegenskaperna när deras temperaturförändring, tillämpas inom områdena geologi, konstruktion, konstruktion av material och i livsmedelsvetenskap.

Det har tillämpats, även om det med viss kritik är Arrhenius -ekvationen i kinetiken för fasta tillståndsreaktioner. Det har också använts för att karakterisera växternas svar på vattenspänning.

Arenhius -ekvationen tjänade som grund för skapandet av en matematisk modell, vilket kvantifierar effekten av temperaturen på användbarheten för nickelmetalliska hydridceller eller batterier.

På samma sätt, baserat på Arrhenius -ekvationen, fastställdes nedbrytningshastigheten för svinavfall och matolja, under olika fuktinnehåll.

Löst övningar

Övning 1

Vad är aktiveringsenergin för en reaktion om det konstateras att dess hastighetskonstant tripplar när temperaturen stiger från 600 K till 610 K?

Kan tjäna dig: fenoxyättiksyra: syntes, procedur, användningar, risker

Börjar från Arrhenius -ekvationen:

k = a · e^-Ea/rt

Vi rensar faktorn a:

A = k₁ / (E^-Ea/rt1)

Men eftersom vi har två temperaturer, t₁ och t₂, Det kommer att finnas två hastighetskonstanter: k₁ och k₂. Faktor A förändras inte, så vi kan matcha det för den andra temperaturen:

k₁ / (E^-Ea/rt1) = k₂ / (E^-Ea/rt2)

Och clearing e_till vi kommer att ha:

OCH_till = R (ln k₂/k₁) / (1 / t₁ - 1/t₂)

Som vad₂ är tre gånger större än k₁,

k₂ / k₁ = 3

ln (3) = 1.099

Och å andra sidan:

1 / t₁ = 1/600 K = 1.66 x 10^-3 K^-1

1 / t₂ = 1/610 K = 1.64 x 10^-3 K^-1

Ersätter då:

OCH_till = (8.31 J · K^-1· Mol^-1) (1.099) / (1.66 x 10^-3 K^-1 - 1.64 x 10^-3 K^-1)

= 456.5 kJ · mol^-1

Övning 2

I en gasfasreaktion är aktiveringsenergin lika med 103 kJ/mol, och hastighetskonstanten är 0.085 min^-1. Beräkna hastighetskonstanten vid 323 K.

Från det föregående uttrycket rensar vi ln k₂/k₁:

ln k₂/k₁ = (E_till/R) (1 /t₁ - 1/t₂)

Utveckla den högra delen av ekvationen:

ln k₂/k₁ = (103.000 j · mol^-1 / 8.31 J · K^-1· Mol^-1) (1/273 K - 1/323 K)

ln k₂/k₁ = 6.99

Tar antilogaritmer:

k₂/k₁ = 1.086

k₂ = (k₁) (1.086)

= (0.085 min^-1) (1.086)

= 0.092 min^-1

Referenser

1. Whitten, Davis, Peck & Stanley. (2008). Kemi. (8: e upplagan.). Cengage Learning.
2. Walter J. Moore. (1963). Fysisk kemi. I kemisk kinetik. Fjärde upplagan, Longmans.
3. Iran. Levin. (2009). Principer för fysikalik. Sjätte upplagan. MC Graw Hill.
4. Wikipedia. (2020). Arrhenius ekvation. Hämtad från: i.Wikipedia.org
5. Guenevieve del Mundo et al. (10 september 2020). Arrhenius ekvation. Återhämtad från: kem.Librettexts.org
6. Clark Jim. (2013). Hastighetskonstanter och Arrhenius -ekvationen. Återhämtat sig från: Chemguide.co.Storbritannien
7. Redaktörerna för Enyclopaedia Britannica. (2020). Arrhenius ekvation. Återhämtat sig från: Britannica.com
8. Helmestine, Anne Marie, PH.D. (28 augusti 2020). Arrhenius -ekvationsformeln och exemplet. Återhämtat sig från: tankco.com