Henderson-Haselbalch-ekvationsförklaring, exempel, träning
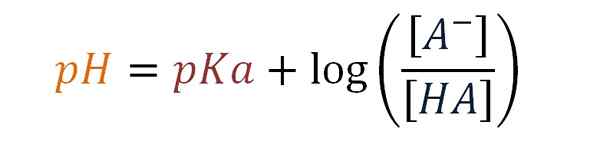
- 2244
- 613
- Karl Johansson
De Henderson-Haselbalch-ekvation Det är ett matematiskt uttryck som möjliggör beräkning av pH för en stötdämpare eller dämpningslösning. Det är baserat på PKA för syra och förhållandet mellan konjugat eller salt- och syrakoncentrationer, närvarande i dämpningslösningen.
Ekvationen utvecklades ursprungligen av Lawrence Joseph Henderson (1878-1942) 1907. Denna kemist etablerade komponenterna i dess ekvation baserat på kolsyra som en buffert eller buffertlösning.
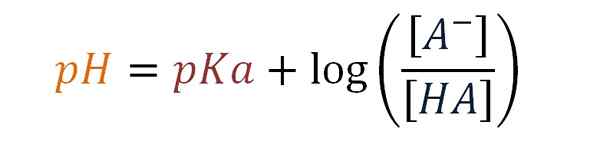 Henderson-Haselbalch-ekvation. Källa: Gabriel Bolívar.
Henderson-Haselbalch-ekvation. Källa: Gabriel Bolívar. Därefter introducerar Karl Albert Hasselbalch (1874-1962) 1917 användningen av logaritmer för att komplettera Henderson-ekvationen. Den danska kemisten studerade blodreaktioner med syre och effekten på hans pH.
En buffertlösning kan minimera pH -förändringar som lider av en lösning genom att lägga till en stark syra eller basvolym. Den bildas av en svag syra och dess starka konjugerade bas som snabbt är dissocierad.
[TOC]
Förklaring
Matematisk utveckling
En svag syra i en vattenhaltig lösning dissocierar enligt massaktionslagen, enligt följande schema:
Ha +h2Eller ⇌ h+ + TILL-
Ha är svag syra och- Din konjugerade bas.
Denna reaktion är reversibel och har en jämviktskonstant (KA):
Ka = [h+] · [Till-] / [Ha]
Tar logaritmer:
log ka = log [h+] +Log [a-] -log [ha]
Om varje term i ekvationen multipliceras med (-1) uttrycks det på följande sätt:
- log ka = - log [h+] -log [a] +log [ha]
- Log Ka definieras som PKA och - loggen [h+] definieras som pH. Efter att ha gjort rättvisning reduceras matematiskt uttryck till:
pKa = ph -log [a-] +Log [ha]
Rensning av pH och omgrupperingsvillkor uttrycks ekvationen på följande sätt:
Kan tjäna dig: trippel kovalent länkph = pka +log [a-] / [Ha]
Detta är Henderson-Haselbalch-ekvationen för en stötdämpare som bildas av en svag syra.
Ekvation för en svag bas
På liknande sätt kan en svag bas bilda en buffertlösning och Henderson-Haselbalch-ekvationen för den är som följer:
POH = PKB +LOG [HB] / [B-]
De flesta dämpningslösningar har emellertid sitt ursprung, inklusive de av fysiologisk betydelse, från dissociation av en svag syra. Därför är det mest använda uttrycket för Henderson-Haselbalch-ekvationen:
ph = pka +log [a-] / [Ha]
Hur agerar en buffertlösning?
Stötdämpare
Henderson-Haselbalch-ekvationen indikerar att denna lösning bildas av en svag syra och en stark konjugerad bas uttryckt som salt. Denna komposition gör att dämpningslösningen kan förbli med ett stabilt pH, även om starka syror eller baser läggs till.
Genom att tillsätta en stark syra till stötdämparen reagerar den med den konjugerade basen för att bilda ett salt och vatten. Detta neutraliserar syran och gör att variationen av pH är minimal.
Nu, om en stark bas läggs till stötdämparen, reagerar den med svag syra och vattenform och salt och neutraliserar verkan av den tillagda basen på pH. Därför är pH -variation minimal.
PH för en buffertlösning beror på förhållandet mellan konjugatbaskoncentrationer och svag syra, och inte på det absoluta värdet på koncentrationerna av dessa komponenter. En dämpningslösning med vatten kan spädas ut och pH kommer praktiskt taget inte att variera.
Stötdämpare kapacitet
Dämpningskapaciteten beror också på PKA för svag syra, liksom koncentrationerna av svag syra och konjugatbas. Ju närmare syran PKA är pH för dämpningslösningen, desto större är dess dämpningskapacitet.
Kan tjäna dig: Le Châtelier -principenJu större koncentrationen av komponenterna i buffertlösningen, desto större kommer dess dämpningskapacitet att vara.
Henderson Equations Exempel
Acetatbuffert
ph = pka +log [cho3Kuttra-] / [Cho3Cooh]
PKA = 4,75
Karbonsyra amortide
ph = pka +log [hco3-] / [H2Co3]
PKA = 6.11
Den globala processen som leder till bildandet av bikarbonatjonen i en levande organisme är emellertid följande:
Co2 + H2Eller ⇌ hco3- + H+
Vara co2 En gas, dess koncentration i lösningen uttrycks enligt dess partiella tryck.
ph = pka +log [hco3-] / α · PCO2
α = 0,03 (mmol/L)/mmHg
Pco2 är CO: s partiella tryck2
Och då skulle ekvationen vara som:
ph = pka +log [hco3-] / 0,03 · PCO2
Laktat stötdämpare
pH = pKa +log [laktatjon] / [mjölksyra]
PKA = 3,86
Fosfat stötdämpare
pH = pKa +log [dibasiskt fosfat] / [monobasiskt fosfat]]]
ph = pka +log [HPO42-] / [H2Po4-]
PKA = 6,8
Oxihemoglobin
ph = pka +log [HBO2-] / [HHBO2]
PKA = 6,62
Desoxyhemoglobin
ph = pka +log [HB-] / Hbh
PKA = 8.18
Löst övningar
Övning 1
Fosfatschötdämparen är viktig vid regleringen av kroppens pH, eftersom dess PKA (6.8) är nära pH i kroppen (7,4). Vad är värdet av förhållandet [na2Hpo42-] / [Nah2Po4-] av Henderson-Haselbalch-ekvationen för ett värde på pH = 7,35 och en PKA = 6,8?
NAH: s dissocieringsreaktion2Po4- är:
Nej2Po4- (syra) ⇌ nahpo42- (Bas) +h+
ph = pka +log [na2Hpo42-] / [Nah2Po4-]
Rensa [konjugerad / syra] -förhållandet för fosfatdämpningslösningen har vi:
7.35 - 6.8 = log [na2Hpo42-] / [Nah2Po4-]
0,535 = log [na2Hpo42-] / [Nah2Po4-]
100,535 = 10Log [Na2HPO4] / [NAH2PO4]
Det kan tjäna dig: difenylamin3.43 = [na2Hpo42-] / [Nah2Po4-]
Övning 2
En acetatbuffertlösning har en 0,0135 M ättiksyrakoncentration och en 0,0260 M natriumacetatkoncentration. Beräkna pH för stötdämparen, och veta att PKA för acetatchockabsorberaren är 4,75.
Dissociationsbalansen för ättiksyra är:
Ch3COOH ⇌ Ch3Kuttra- + H+
ph = pka +log [cho3Kuttra-] / [Cho3Cooh]
Ersätta de värden vi har:
[Ch3Kuttra-] / [Cho3COOH] = 0,0260 m / 0,0135 m
[Ch3Kuttra-] / [Cho3COOH] = 1 884
Log 1.884 = 0,275
pH = 4,75 +0,275
pH = 5,025
Övning 3
En acetat stötdämpare innehåller 0,1 m ättiksyra och 0,1 M natriumacetat. Beräkna pH för dämpningslösningen efter tillsats av 5 ml 0,05 M vid 10 ml saltsyra.
Det första steget är att beräkna den slutliga koncentrationen av HCL vid blandning med buffertlösningen:
Vi · ci = vf · cf
CF = vi · (CI / VF)
= 5 ml · (0,05 m / 15 ml)
= 0,017 m
Saltsyra reagerar med natriumacetat för att bilda ättiksyra. Därför minskar natriumacetatkoncentrationen med 0,017 M och ättiksyrakoncentrationen ökar med samma mängd:
pH = PKA +log (0,1 m - 0,017 m) /(0,1 m +0,017 m)
pH = PKA +log 0,083 / 0,017
= 4,75 -0.149
= 4 601
Referenser
- Whitten, Davis, Peck & Stanley. (2008). Kemi. (8: e upplagan.). Cengage Learning.
- Jimenez Vargas och J. Mª macarulla. (1984). Fysiologisk fysisk -kemisk. Sjätte upplagan. Inter -amerikansk redaktion.
- Wikipedia. (2020). Henderson-Hasselbalch-ekvation. Hämtad från: i.Wikipedia.org
- Gurinder Khaira & Alexander Kot. (5 juni 2019). Henderson-Hasselbalch approximation. Kemi librettexts. Återhämtad från: kem.Librettexts.org
- Helmestine, Anne Marie, PH.D. (29 januari 2020). Henderson Hasselbalch Equation Definition. Återhämtat sig från: tankco.com
- Redaktörerna för Enyclopaedia Britannica. (6 februari 2020). Lawrence Joseph Henderson. Encyclopædia Britannica. Återhämtat sig från: Britannica.com
- « Förordsegenskaper, funktioner, exempel och delar
- Foundation Refractometry, Refractiers Typer, Applications »

