Ellips

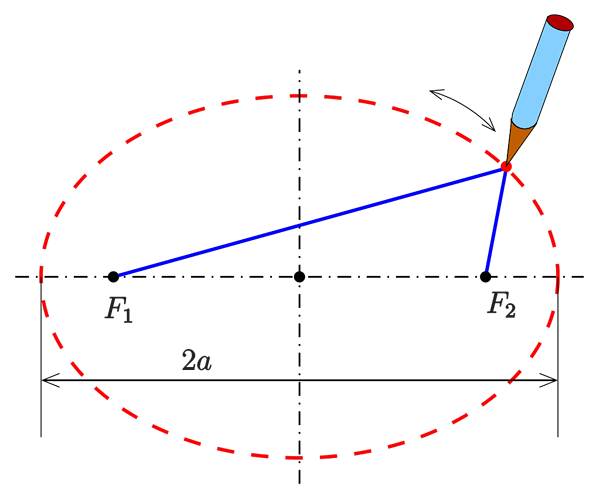
Figur 1. Gardener Method för att rita en ellips. Summan av avstånden mellan en punkt P för ellipsen (i rött) och strålkastarna (i svart) förblir konstant. Källa: AG2GAEH, CC BY-SA 4.0, via Wikimedia Commons.

Vad är en ellips?

En ellips är en uppsättning koordinatpunkter (x, y), för vilken summan av avståndet till två fasta punkter, kallas Focos, det är konstant. I sin tur separeras strålkastarna från varandra ett avstånd lika med 2C.

Elliperna finns i naturen. Till exempel är det i jordens rörelse runt solen, eftersom det visas av tyska astronomi.

Dessutom finns den elliptiska formen i utformningen av arkitektoniska konstruktioner, är en del av en medicinsk behandling för att förstöra njurberäkningar och tjänar till att forma olika föremål som tankar och andra containrar.

I den övre figuren visas en ellips med sina två strålkastare, belägna lika från figurens centrum och på den längsta axeln. Villkoret att en punkt P måste möta för att tillhöra ellipsen är att summan av avståndet till varje fokus är fixat:

d₁ + d₂ = konstant.

Därför, när en trädgårdsmästare vill. Ta sedan ett rep med god storlek, bind sina ändar till insatserna och stödja en pinne på repet glider den på den för att markera det elliptiska spåret på den mjuka jorden. Det här är trädgårdsmetod Att rita ellips.

Elementelement

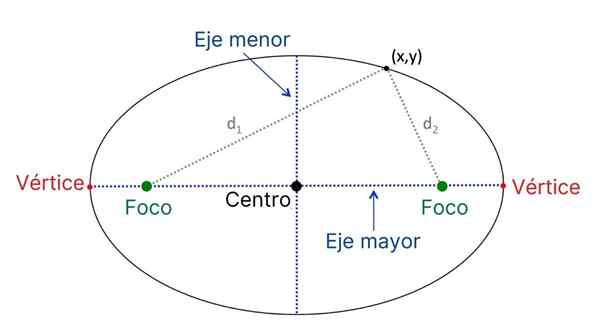Huvudelement i en ellips

Dessa är de viktigaste elementen i ellipsen:

1. Focos, Fasta punkter belägna på ellipsens längsta axel.
2. Häckar, De är de två punkterna i ellipsen genom vilken linjen passerar som går med i strålkastarna.
3. Huvudaxel, Det är repet som ansluter sig till topparna och också innehåller strålkastarna.
4. Centrum, Mittpunkten för huvudaxeln, som motsvarar koordinatpunkten (h, k). Varje fokus är likvärdigt från mitten och på avstånd c av samma.
5. Mindre axel, Det är repet som passerar genom mitten och är vinkelrätt mot huvudaxeln.
6. Vektorradio, segment som förenar var och en fokuserar med en ellips.
7. Fokalaxel, rakt på vilka strålkastarna är.
8. Brännvidd, Det är avståndet mellan strålkastarna, betecknade som 2c.
9. Sugsxel, Axis vinkelrätt mot huvudaxeln, som samtidigt är mediatrix av segmentet som binder till strålkastarna.
10. Symmetricentrum, punkt sammanfaller med ellipsens centrum, där symmetrixarna är korsade.
11. Symmetriaxlar, linjer som innehåller de största och mindre axlarna i ellipsen.

Kan tjäna dig: beskattning

Typer av ellips

Det finns två typer av ellips:

• De som har horisontella huvudaxeln.
• De som har den största vertikala axeln.

Sedan beskrivs de matematiskt:

Ellips med den stora horisontella axeln

Låt punkt C för koordinater (h, k) ellipsens mitt, längden på huvudaxeln är 2a och längden på den mindre axeln lika med 2b, med en> b.

Ekvationen för denna ellips är:

Ellips med den stora vertikala axeln

Med samma parametrar för ellipsen med en horisontell axel är ellipsen med den huvudsakliga vertikala axeln skriven som:

I båda fallen är avståndet från fokus till centrum c Det är relaterat till sedimenten major och mindre genom:

c² = a² - b²

Exempel på ellips

Horisontell ellips

Följande bild visar en ellips vars huvudaxel är horisontellt. Centret är vid punkt (0,0) och strålkastarna i (-3.0) respektive (3.0). Punkt P (0, -4) markerad tillhör ellipsen.

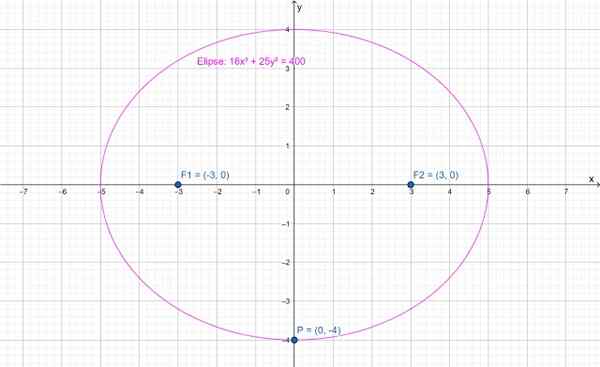figur 2.- Ellips vars huvudaxel är horisontell. Källa: f. Zapata genom geogebra.

Ekvationen för denna ellips är:

16x² + 25 och² = 400

Det är inte svårt att uttrycka denna ekvation i den kanoniska formen, det räcker för att dela alla termer mellan 400 och förenkla bekvämt (se övningen löst senare).

Vertikal ellips

Följande är en vertikal ellips, vars huvudaxel sammanfaller med axeln och. Det är fokuserat på punkt (0,0) och dess ekvation är:

36x² + 9y² = 324

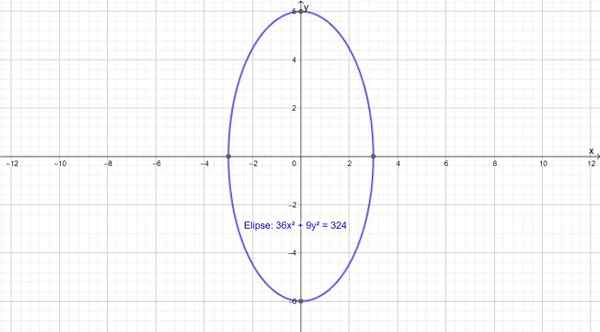Figur 3.- En ellips med den stora vertikala axeln. Källa: f. Zapata genom geogebra.

Reflektionsegenskap

Den består av följande: Om en reflektor eller en ljudkälla placeras i en av ellipsens strålkastare reflekteras de utsända vågorna mot det andra fokuset. Det är ett bra sätt att omdirigera vågorna där din energi behövs.

Kan tjäna dig: endecagon

Det är därför i de elliptiska hallarna, när en person talar att vara i en av strålkastarna, lyssnar en lyssnare i den andra fokusen tydligt.

Och inom medicin används denna reflektionsegenskap för att förstöra njursten genom att sätta patienten i en av strålkastarna på ett elliptiskt badkar fullt av vatten, medan ultraljudsvåggeneratorn är placerad i det andra fokuset. Vågorna återspeglas i beräkningarna och fragmenterar dem i mindre partiklar, som sedan utvisas genom urinen.

SKA -radioen

Detta radioteleskop är det största i sin typ och förväntas börja arbeta 2021. Ytan är 1 km kvadrat och det är därför det kallas ska (på engelska är de förkortningen för Fyrkantig kilometer matris).

Genom att utnyttja ellipsens reflektionsegenskaper består strukturen av ett arrangemang av 3000 antenner med elliptisk form av cirka 15 m bred, fördelad mellan Australien och Sydafrika. Med detta instrument, 50 gånger mer känsliga än de som används just nu, förväntas det titta på universum när det fortfarande var mycket yngre: ungefär en miljard år knappt.

Figur 4.- Konstnärlig tolkning av ska radio Ska. Källa: Wikimedia Commons.

Träning löst

Hitta de kanoniska ekvationerna för elliperna som visas i figurerna 2 och 3 och i båda fallen bestämmer längden på sinnena större och mindre, såväl som fokala avstånd.

Lösning

För den horisontella ellipsen, vars ekvation är 16x² + 25 och² = 400, alla termer mellan 400 är uppdelade, vilket resulterar:

Kan tjäna dig: Cotangent härledd: beräkning, demonstration, övningar

 Vilket är förenklat:

Semi -axeln "A" mäter 5 och de minsta "B" mäter 4, som också varnas genom att observera bilden noggrant. När det gäller fokalavståndet måste du:

c² = a² - b²

c² = 25 - 16 = 9 ⇒ C = √9 = 3

Därför är C = 3 avståndet mellan centrum och en av strålkastarna. Båda foci är ett avstånd 2c = 6.

När det gäller den vertikala ellipsen 36x² + 9y² = 324 Du har:

Genom att förenkla:

c² = 36 - 9 = 27

C = √27 ≅ 5.2

Därför är avståndet mellan strålkastarna 10.4 enheter.

Referenser

1. Hoffman, J. Urval av matematikfrågor. Volym 3.
2. Stewart, J. 2006. Preccculment: Matematik för beräkning. Femte. Utgåva. Cengage Learning.
3. Universumsformler. Ellipsen. Återhämtat sig från: universalformulor.com.
4. Wikipedia. Fyrkantig kilometer matris. Återhämtad från: är.Wikipedia.org.
5. Zill, D. 1984. Algebra och trigonometri. McGraw Hill.