I vilka situationer som är linjära och kvadratiska funktioner?

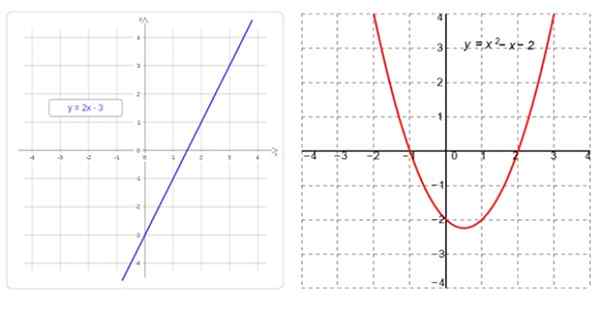
Till vänster en linjär funktion, vars graf är en rak linje, och till höger, en kvadratisk funktion, vars graf är en parabola. Källa: f. Zapata

Vad är linjära och kvadratiska funktioner?

Linjära funktioner och kvadratiska funktioner är funktioner som tillhör gruppen Polynomic Functions. De används för att modellera olika situationer, till exempel beroendet mellan volymen och vikten på en kropp, mängden och kostnaden för en produkt, position kontra tid och mer.

I allmänhet är en funktion en relation som länkar två variabler och kan användas för att modellera den verkliga världen. Polynomfunktioner, som namnet antyder, uttrycks genom ett polynom, vars allmänna form är:

f (x) = a_nxⁿ + till _N-1x ^N-1 + till_X-2x^N-2 +Till ... till_antingen

Där n är ett naturligt antal, siffrorna till₀, till₁, till₂,Till ... till_n De är verkliga, till₀ Det är den oberoende termen och till_n, Det är koefficienten som följer med den högsta kraften. Värdet på n indikerar vilken typ av funktion, för n = 1 Funktionen är linjär, medan för n = 2 funktionen är kvadratisk.

I det första av dessa fall reduceras det allmänna uttrycket till:

f (x) = a₁x + a_antingen

Och i det andra fallet kvarstår det så här:

f (x) = a₂x² + till₁x + a_antingen ;   (till₂≠ 0)

Graferna för polynomfunktionerna är kontinuerliga, det vill säga de upplever inte plötsliga hopp eller brister och har därmed mjukt beteende, utan oegentligheter. Därför observeras de vid modellering av många situationer inom vetenskap, ekonomi och andra områden med mänsklig kunskap.

Därefter beskrivs intressanta tillämpningar av varandra mer detaljerat.

Situationer där linjära funktioner visas

Den linjära funktionen representeras algebraiskt av:

f (x) = a₁x + a_antingen

Eller motsvarande:

f (x) = mx + b

Dess distinkta funktion är att dess graf är en rak linje. Värdet m, vilket är koefficienten för x, representerar den örhänge av denna linje och ger ett mått på hur lutande det är.

Kan tjäna dig: Icke -linjär programmering: Metoder och övningar

Lutningen kan vara positiv, negativ eller noll, men den är alltid konstant, det vill säga dess växelkurs förblir oförändrad.

En linje med lutning 0 är helt horisontell, den för positiv lutning indikerar höjd eller ökning (om en av variablerna ökar, den andra också, alltid i samma takt) och slutligen indikerar den negativa lutningen minskning (som en av variablerna ökar, den andra minskar).

Värdet av b, För sin del representerar det skärningen eller skärningspunkten i linjen med den vertikala axeln. Ja B = 0, Linjen går genom koordinatsystemets ursprung.

Modelleringsexempel med linjära funktioner

1. Den enhetliga rätlinjiga rörelsen

Ekvationen som länkar X -positionen och tiden T för en mobil, i den enhetliga rätlinjiga rörelsen, är linjär:

x (t) = v⋅t + x_antingen

Där v, lutningen på linjen, är mobilens hastighet, som förblir konstant under hela rörelsen, och x_antingen är den första positionen.

2. Densitet

Ett objekts densitet eller ett ämne, som fastställer förhållandet mellan massa och volym. Ringer ρ till densiteten (den lyder "rho"), m till degen och v till volymen, du har:

Rensa degen, när det gäller volymen, den erhålls:

M = ρv

Vid grafering av degen beroende på volymen erhålls en rak linje vars lutning är föremålets täthet eller substans.

3. Längd på en omkrets

Konturen i en cirkel, eller dess längd, är proportionell mot dess radie. Detta innebär att ju större radie, desto större kontur är omkretsen enligt ekvationen:

Kan tjäna dig: korrelationskoefficient: formler, beräkning, tolkning, exempel

C = 2πr

Där C är kontur eller längd är R radio och π (läser “pi”) är en konstant vars ungefärliga värde är πamp3.14 ..

4. Kostnad för att skicka ett paket

Eftersom det är lätt att dra, är den tyngre eller skrymmande en dyrare paket att transportera det. Företag som är dedikerade till lasttransport modellerar sina priser efter vissa regler, till exempel:

C (x) = 2.75x

I denna ekvation är C (x) dollarkostnaden för att skicka ett paket vars vikt är x pund. Konstantvärdet 2.75 har enheter av dollar/pund (enhetskostnad).

Situationer där kvadratiska funktioner visas

Algebraiskt representeras en kvadratisk funktion av:

f (x) = a₂ x² + till₁ x + a_antingen

Med villkoret att koefficienten för₂ Vara annorlunda än 0. Den kännetecknas av dess parabola -formade graf, vars axiella axel eller symmetriaxel är vertikal (parallell med y -axeln)))).

Korsningen mellan liknelsen och den nämnda axeln är en punkt som heter Vertex. Om liknelsen öppnas (a₂ > 0), toppen är dess minsta punkt, och om den öppnas (a₂ < 0), es el máximo.

På symmetriaxeln är fokus, en speciell punkt som bestämmer krökningen av parabolen. Om solljus påverkas på en parabolisk spegel kommer strålarna att reflekteras på ytan, sammanfaller i fokus, som värms omedelbart.

Modelleringsexempel med kvadratiska funktioner

1. Höjden på en projektil som lanseras vertikalt upp

En projektil är alla objekt som en initial hastighet tillhandahålls och sedan släpps under tyngdkraften. Om den initiala hastigheten är vertikal, storlek V₀ och riktad upp kommer objektet att stiga till en maximal höjd och sedan sjunka ner.

Kan tjäna dig: homotecia

Ekvationen för höjd h som en funktion av tiden t är:

H (t) = −4.9 T²+v₀ t

Där den vertikala känslan tas som positiv och den vertikala nere negativa.

2. Banan för en horisontell eller sned projektil

Om en horisontell eller sned initial hastighet tillhandahålls till en projektil kommer den att beskriva en parabolisk bana, som kan representeras genom en kvadratisk funktion som tidigare beskrivits.

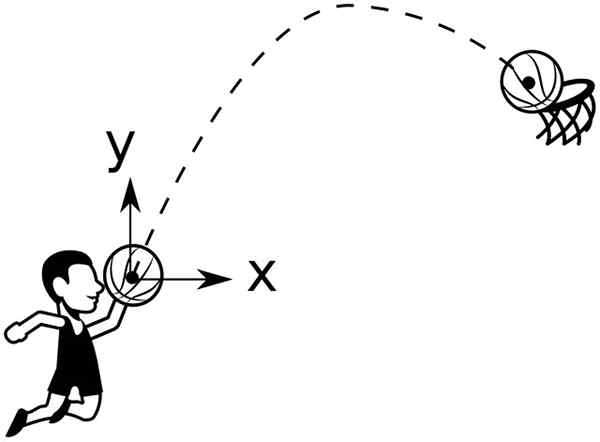Basket's Ball beskriver en parabolisk bana som ska kastas i korgen. Källa: Wikimedia Commons

Till exempel en boll som kastas från en höjd och₀, bildningsvinkel θ₀ När det gäller horisontellt har den en bana som ges av:

Med g som tyngdkraften, som kan ungefär 10 m/s². Till exempel en fotbollspark från marken (och₀ = 0), med initial hastighet på 6 m/s och vinkel på 45º med avseende på horisontellt, kommer att ha en bana som ges av följande liknelse:

3. Området i en cirkel

Ju högre cirkelens radie, desto större är dess område att vara. Faktum är att cirkelområdet är proportionellt mot kvadratet för radien R, varvid proportionalitetens konstant är antalet π:

A = πr²

4. Effektiviteten av en annons

Ju mer de ser det, desto effektivare en kommersiell annons. Effektivitet E, på en skala från 0 till 10, från ett meddelande kan modelleras enligt följande kvadratiska funktion:

Referenser 

1. Polynomfunktioner. Återhämtat sig från resurser.utbildning.är.
2. Larson, r. (2012). Förkalkning. 8th. utgåva. Cengage Learning.
3. Miller, c. (2013). Matematik: resonemang och tillämpningar. 12th. utgåva. Pearson Education.
4. Stewart, J. (2012). Förkalkning. Matematik för beräkning. Sjätte. utgåva. Cengage Learning.
5. Zill, D. (2008). Preccculment med beräkningsförskott. 4th. utgåva. McGraw Hill.