Elektromagnetisk energiformel, ekvationer, användningar, exempel

De Elektromagnetisk energi Det är en som sprider sig genom elektromagnetiska vågor (EM). Exempel på detta är solljuset som utstrålar värme, strömmen som extraheras från det elektriska utloppet och det som X -Rays måste producera röntgenbilder.

Liksom ljudvågor när de gör trumhinnan vibrera, är elektromagnetiska vågor kapabla att överföra energi som senare kan bli värme, elektriska strömmar eller olika signaler.

Figur 1. Antenner är nödvändiga i telekommunikation. Tecken som de arbetar har elektromagnetisk energi. Källa: Pixabay.

Elektromagnetisk energi förökas både i en materiell och tomhetsmiljö, alltid i form av en tvärgående våg och att använda den är inte något nytt. Solljus är den primära källan till elektromagnetisk energi och den äldsta kända, men att använda elektricitet är något nyare.

Det var precis 1891 när Edisonföretag Sätt i drift Den första elektriska installationen i Vita huset i Washington DC. Och att som ett komplement till gasbaserade lampor som användes vid den tiden, för till en början fanns det tillräckligt med skepsis när det gäller användning.

Sanningen är att även på de mest avlägsna och saknade platserna fortsätter den elektromagnetiska energin som anländer oändligt från rymden kontinuerligt att upprätthålla den dynamik vi kallar vårt hem i universum.

[TOC]

Formel och ekvationer

Elektromagnetiska vågor är tvärgående vågor, där det elektriska fältet OCH och magnetfältet B De är vinkelräta mot varandra och är också förökningsriktningen för vågen vinkelrätt mot fälten.

Alla vågor kännetecknas av deras frekvens. Det är det breda utbudet av frekvenser av EM -vågor, vilket ger dem mångsidighet när man förvandlar sin energi, vilket är proportionellt mot frekvensen.

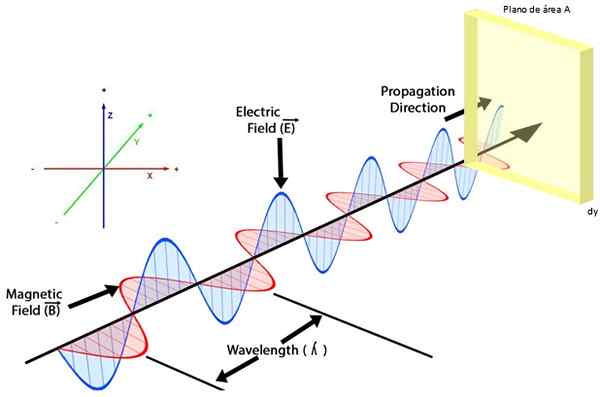
Figur 2 visar en elektromagnetisk våg, i den elektriska fältet OCH I blått oscillerar i planet zy, Magnetfältet B i rött gör det det i planet Xy, Medan våghastigheten riktas längs axeln +och, Enligt det visade koordinatsystemet.

figur 2. En elektromagnetisk våg som påverkar en yta levererar energi enligt Poyning -vektorn. Källa: f. Zapata.

Om på båda vågorna är en yta, låt oss säga ett områdesplan TILL och tjocklek Dy, så att det är vinkelrätt mot våghastigheten, det elektromagnetiska energiflödet per areenhet, betecknad S, beskrivs genom Poyningvektor:

S = (1 /μ_antingen) OCH × B

μ_antingen Det är permeabiliteten för vakuumet (μ_antingen = 4π .10^-7 Tesla. Metro/Ampere), En konstant relaterad till den lätthet som mediet ger till den elektromagnetiska vågen för att röra sig.

Kan tjäna dig: vit dvärg

Poynings vektor introducerades av engelska astrofysiker John Henry Poyning 1884, en pionjär inom energistuden av elektriska och magnetfält.

Omedelbar kraft per enhetsenhet

Nu måste vi ta hänsyn till att energi är en skalar, medan S Det är en vektor.

Kom ihåg att kraften är den energi som levereras per tidsenhet och sedan modulen för S Indikerar Omedelbar kraft per enhetsenhet I riktning mot utbredningen av den elektromagnetiska vågen (energiöverföringshastighet).

Eftersom OCH och B De är vinkelräta mot varandra, modulen för OCH x B Det är helt enkelt EB Och omedelbar kraft (en skalar) kvarstår:

S = (1 /μ_antingen) EB

Det är lätt att verifiera att S -enheter är watt/m² I det internationella systemet.

Det finns fortfarande mer. Fältets storlek OCH och B De är relaterade till varandra genom ljusets hastighet c. Faktum är att elektromagnetiska vågor i vakuum sprids så snabbt. Detta förhållande är:

E = CB

Att ersätta detta förhållande i S erhålls:

S = (1 /μ_antingen.Ec²

Poyning -vektorn varierar med sinusformad tiden, så det föregående uttrycket är dess maximala värde, eftersom den energi som levereras av den elektromagnetiska vågen också svänger, precis som fälten gör. Naturligtvis är svängningsfrekvensen mycket stor, så det är inte möjligt att upptäcka den i synligt ljus, till exempel.

Ansökningar

Bland de flera användningsområden som vi redan har sagt har elektromagnetisk energi, här är två som kontinuerligt används i många applikationer:

Dipoloantenn

Antennerna är överallt att fylla utrymmet med elektromagnetiska vågor. Det finns sändare som omvandlar elektriska signaler till radio- eller mikrovågsvågor, till exempel. Och det finns receptorer, som gör det omvända arbetet: de samlar in vågorna och gör dem till elektriska signaler.

Låt oss se hur man skapar en elektromagnetisk signal som sprider sig i rymden, från en elektrisk dipol. Dipolen består av två elektriska laddningar av lika stor storlek och motsatta tecken, åtskilda med ett litet avstånd.

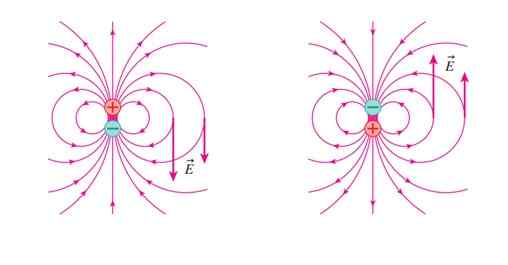
Kan tjäna dig: elektriska ledare

I följande figur är det elektriska fältet OCH När lasten + är uppe (vänster figur). OCH pekar ner vid den visade punkten.

Figur 3. Elektriskt fält av en dipol i två olika positioner. Källa: Randall Knight. Fysik för forskare och ingenjörer.

I figur 3 till höger ändrade dipolen position och nu OCH pekar på. Vi upprepar denna förändring många gånger och mycket snabbt, låt oss säga frekvens F. Ett fält skapas så OCH Variabel i tid ger upphov till ett magnetfält B, också variabel och vars form är sinus (se figur 4 och nedan exempel 1).

Och hur Faradays lag säkerställer att ett magnetfält B Variabel i tid ger upphov till ett elektriskt fält, eftersom det visar sig att att göra dipolen redan har ett elektromagnetiskt fält som kan spridas.

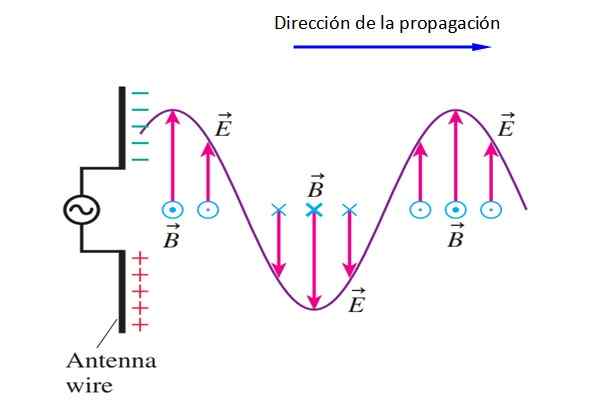Figur 4. En dipolantenn genererar en signal som transporterar elektromagnetisk energi. Källa: f. Zapata.

Jag känner att B punkter inuti eller utanför skärmen växelvis (det är alltid vinkelrätt mot OCH).

Elektrisk fältenergi: kondensorn

Kondensatorerna har dygden att lagra elektrisk laddning och därför elektrisk kraft. De är en del av många enheter: motorer, radio- och tv -kretsar, billjussystem och mycket mer.

Kondensatorerna består av två separata förare ett litet avstånd. Var och en tilldelas en belastning med lika stor storlek och motsatt skylt och skapar sedan ett elektriskt fält i utrymmet mellan de två förarna. Geometrien kan variera och vara en välkänd den för den platt-parallella plackkondensatorn.

Energin lagrad i en kondensor kommer från det arbete som gjordes för att ladda det, vilket tjänade till att skapa det elektriska fältet inuti. Introduktion av ett dielektriskt material mellan plattorna ökar kondensatorns kapacitet och därför den energi som detta kan lagra.

En kapacitetskondensator och initialt urladdad, som laddas av ett batteri som levererar en V -spänning, tills den når en Q -belastning, lagrar en energi eller ges av:

U = ½ (q²/C) = ½ QV = ½ cv²

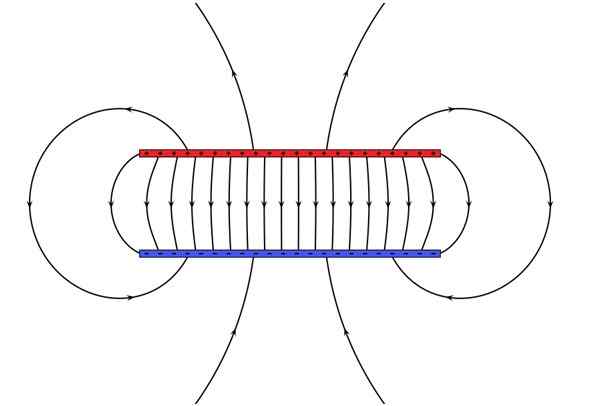Figur 5. En parallell plattplattor kondensor lagrar elektromagnetisk energi. Källa: Wikimedia Commons. Geek3 [CC BY-SA 4.0 (https: // CreativeCommons.Org/licenser/BY-SA/4.0)].

Exempel

Exempel 1: Intensitet av en elektromagnetisk våg

Tidigare sades det att storleken på Poyning -vektorn är ekvivalent med den kraft som vågen levererar för varje kvadratmeter ytan, och att dess tidsberoende vektor är den tidsberoende, dess värde upp till maximalt maximum av S = s = (1 /μ_antingen.Ec².

Medelvärdet på S i en vågcykel är lätt att mäta och indikera vågenergin. Detta värde kallas vågintensitet Och det beräknas på detta sätt:

Kan tjäna dig: vad är dynamisk balans? (Med exempel)

I = s_halv = S = (1 /μ_antingen.Ec²_halv

En elektromagnetisk våg representeras av en sinusfunktion:

E = e_antingen Sen (KX - Ωt)

Var OCH_antingen Det är vågens amplitud, k Vågnumret och Ω Vinkelfrekvensen. Så:

Medelvärdet för SEN -funktionen² X i en cykel är ½. Det beräknas formellt av följande uttryck, vilket är möjligt att verifiera med hjälp av en integrerad tabell eller utföra det integrerade analytiskt:

Därför s_halv Det återstår som:När en källa avger lika i alla riktningar utstrålas kraften enligt det omvända till avståndet till källan (figur 5). Ja P_m Det är den genomsnittliga kraften, då på avstånd r Intensiteten Yo av signalen ges den av:

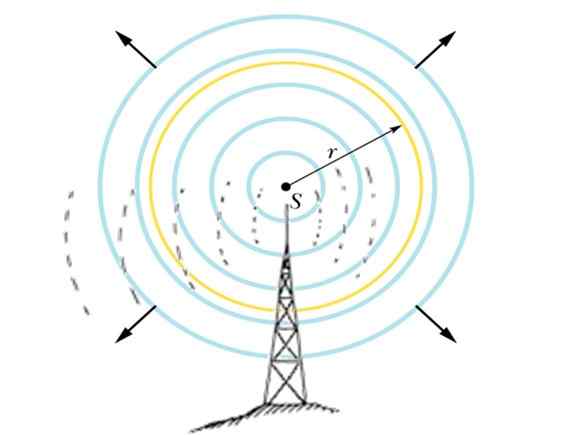Figur 5. Antennen utstrålar signalen i sfärisk form. Källa: f. Zapata.

Exempel 2: Applicering på en sändande antenn

Det finns en radiostation som överför en 10 kW -signal om kraft och frekvens på 100 MHz, som sprider sig i en sfärisk form, som i figuren ovan.

Hitta: a) amplituden hos de elektriska och magnetiska fälten vid en punkt belägen 1 km från antennen och b) den totala elektromagnetiska energin som påverkar ett kvadratblad 10 cm under en period av 5 minuter.

Uppgifterna är:

Lätthastighet i vakuum: C = 300.000 km/s

Vakuumpermeabilitet: μ_antingen = 4π .10^-7 T.m/a (Tesla. Metro/Ampere)

Lösning till

Ekvationen i exempel 1 används för att hitta intensiteten i den elektromagnetiska vågen, men först måste värdena i det internationella systemet uttryckas:

10 kW = 10000 w

100 MHz = 100 x 10⁶ HZ

IR dessa värden ersätts i ekvationen för intensitet, eftersom det är en källa som avger lika (källa isotropisk):

Detta är just den genomsnittliga effekten per enhet av medelområdet eller värdet på Poyning Vector -modulen:

Tidigare sades det att storleken på OCH och B De var relaterade av ljusets hastighet:

E = CB

B = (0.775/300.000.000) t = 2.58 x 10^-9 T

Lösning B

S_halv Det är kraft per enhetsenhet och i sin tur är kraften energi per tidsenhet. Multiplicera S_halv För plattområdet och för exponeringstiden erhålls det begärda resultatet:

5 minuter = 300 sekunder

Område = (10/100)²  m² = 0.01 m².

U = 0.775 x 300 x 0.01 Joules = 2.325 Joules.

Referenser

1. Figueroa, D. (2005). Serie: Physics for Science and Engineering. Volym 6. Elektromagnetism. Redigerad av Douglas Figueroa (USB). 307-314.
2. ICES (internationell kommitté för elektromagnetisk säkerhet). Elektromagnetiska energifakta och en kvalitativ vy. Återhämtat sig från: ices-emfsafety.org.
3. Riddare, r. 2017. Fysik för forskare och teknik: En strategistrategi. Pearson. 893 - 896.
4. Portland State University. Em Waves TRATE ENERGY. Återhämtat sig från: pdx.Edu
5. Vad är elektromagnetisk energi och varför är det viktigt?. Återhämtat sig från: sciencestruck.com.