Potentiella energiegenskaper, typer, beräkning och exempel

De potentiell energi Det är den energi som kropparna har under sin konfiguration. När föremål interagerar finns det krafter som kan göra arbete, och denna förmåga att göra arbete, som lagras i den disposition de har, kan översätta till energi.

Till exempel har människor utnyttjat den potentiella energin från vattenfall sedan urminnes tider, först snurrande fabriker och sedan i vattenkraftverk.

Niagara Falls: En enorm gravitationspotentialenergi reserv. Källa: Pixabay.

Å andra sidan har många material en anmärkningsvärd förmåga att göra arbete genom att deformeras och sedan återvända till sin ursprungliga storlek. Och under andra omständigheter tillåter arrangemanget av den elektriska laddningen att lagra elektrisk potentiell energi, till exempel i en kondensor.

Potentiell energi erbjuder många möjligheter att förvandlas till andra användbara former av energi, därmed vikten av att känna till lagarna som styr den. 

[TOC]

Ursprunget till potentiell energi

En objekts potentiella energi har sitt ursprung i krafterna som påverkar det. Potentiell energi är emellertid en skalär storlek, medan krafter är vektor. För att specificera den potentiella energin räcker det därför för att indikera dess numeriska värde och de valda enheterna.

En annan viktig kvalitet är den typ av kraft som potentiell energi kan lagras, eftersom ingen kraft har denna dygd. Endast konservativa krafter lagrar potentiell energi i de system som de agerar.

En konservativ kraft är den som arbetet inte beror på banan följt av objektet, utan bara på utgångspunkten och ankomstpunkten. Kraften som driver vattenfall är tyngdkraften, vilket är en konservativ kraft.

Å andra sidan har elastiska och elektrostatiska krafter också denna kvalitet, därför finns det potentiell energi associerad med dem.

Krafter som inte uppfyller det ovannämnda kravet, de kallas icke -konservativa; Exempel på dem är i friktion och luftmotstånd.

Typer av potentiell energi

Eftersom potentiell energi alltid härstammar från konservativa krafter som de som redan nämnts är det samtal om gravitationspotential energi, elastisk potentiell energi, elektrostatisk potentiell energi, kärnkraftspotential energi och potentiell energikemisk energi.

Potentiell gravitationsenergi

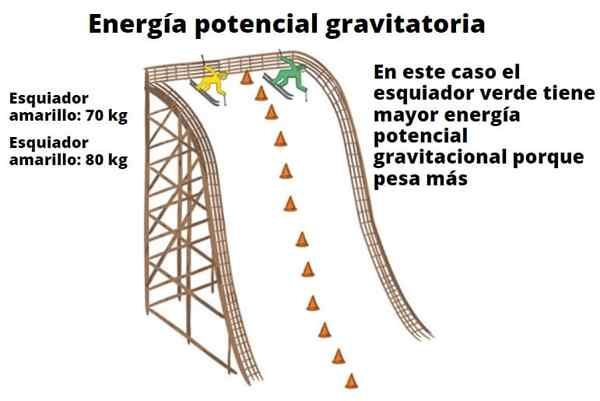
Alla objekt har potentiell energi baserat på den höjd de har med avseende på marken. Detta enkla faktum i utseende, illustrerar eftersom vattenfallet kan öka turbinerna och så småningom förvandlas till el. Exemplet på skidåkare som visas här visar också förhållandet mellan vikt och höjd med gravitationspotential energi.

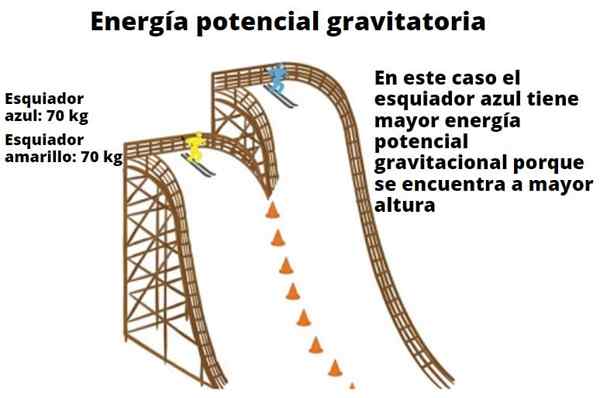
Ett annat exempel är en Roller Mountain -bil, som har större potentiell energi när den är på en viss höjd på marken. När den har nått golvnivån är höjden lika med noll och all dess potentiella energi har förvandlats till kinetisk energi (rörelseenergi).

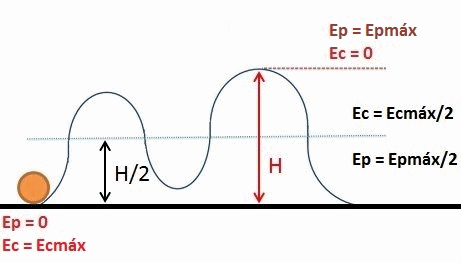Animering visar utbytet mellan gravitationspotential energi och kinetisk energi, av ett objekt som rör sig på en berg -och dalbana. Summan av båda energier, kallad mekanisk energi, är konstant under hela rörelsen. Källa: Wikimedia Commons.

Elastisk potentiell energi

Föremål som fjädrar, bågar, armbågar och ligor kan lagra elastisk potentiell energi.

När bågen spänner gör målvakten ett jobb som lagras som potentiell energi i bågen-fet-systemet. När bågen frigörs förvandlas denna energi till pilens rörelse. Källa: Pixabay.

Elasticiteten hos en kropp eller ett material beskrivs av Hookes lag (upp till vissa gränser), som säger att kraften som kan utöva när den komprimeras eller sträckas, är proportionell mot dess deformation.

Kan tjäna dig: ferromagnetism: material, applikationer och exempel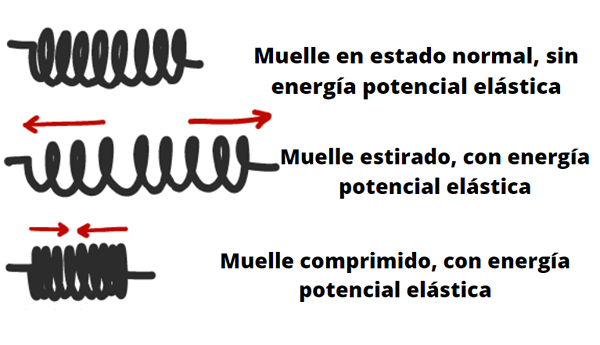

Till exempel vid en vår eller vår, betyder det att ju mer den krymper eller sträcker sig, desto större är kraften som kan utövas på ett objekt placerat i ena änden.

Elektrostatisk potentiell energi

Det är den energi som elektriska laddningar har under deras konfiguration. De elektriska laddningarna för samma skylt avvisas, så för att placera ett par positiva laster - eller negativa - i en viss position måste en extern agent göra arbete. Annars tenderar de att separera.

Detta arbete lagras på det sätt på vilket belastningarna var belägna. Ju närmare belastningarna med samma tecken är, desto större är den potentiella energin som konfigurationen kommer att ha. Det händer tvärtom när det gäller olika teckenbelastningar; När de lockar, ju närmare de är, desto mindre potentiell energi har de.

Kärnkraftsenergi

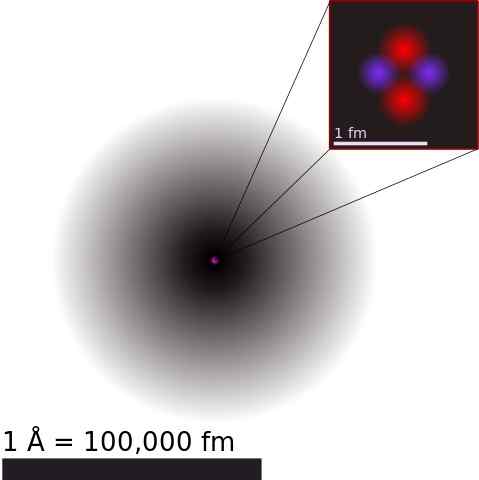Ungefärlig heliumatom. I kärnan representeras protonerna i rött och neutronerna i blått.

Atomarkärnan är sammansatta protoner och neutroner, generellt kallade Nukleoner. Den förstnämnda har positiv elektrisk laddning och de senare är neutrala.

Eftersom de är agglomererade i ett litet utrymme utöver fantasin och att veta att belastningarna på samma tecken är avvisade är det värt att fråga hur atomkärnan förblir sammanhängande.

Svaret är i andra krafter utöver elektrostatisk avstötning, typisk för kärnan, såsom stark kärnkraftsinteraktion och svag kärnkraftsinteraktion. Dessa är mycket intensiva krafter, som långt överstiger elektrostatisk kraft.

Kemisk potentiell energi

Denna form av potentiell energi kommer från hur atomer och ämnen molekyler finns tillgängliga, enligt de olika typerna av kemiska bindningar.

När en kemisk reaktion ges kan denna energi omvandlas till andra typer, till exempel av ett elektriskt batteri eller batteri.

Exempel på potentiell energi

Potentiell energi finns i vardagen i många aspekter. Att observera dess effekter är lika enkelt som att placera alla objekt i en viss höjd och ha säkerheten att det kan rulla eller falla när som helst.

Här är några manifestationer av de potentiella energityperna som tidigare beskrivits:

-Berg-och dalbanor

-Bilar eller bollar som rullar nedförsbacke

-Bågar och pilar

-Elbatterier

-En klocka pendel

När en av de extrema sfärerna är i rörelse överförs rörelsen till de andra. Källa: Pixabay.

-Gunga

-Sprack

-Använd en infällbar penna.

Se: Exempel på potentiell energi.

Potentiell energiberäkning

Den potentiella energin beror på det arbete som gör styrka och detta i sin tur beror inte på banan, då kan det bekräftas att:

-Om A och B är två punkter är arbetet W_Ab  nödvändigt att gå från A till B, det är lika med det nödvändiga arbetet att gå från B till en. Därför: W_Ab = W_Ba, så:

W_Ab + W_Ba = 0

-Och om två olika banor 1 och 2 testas för att gå med i dessa punkter A och B, är arbetet som utförs i båda fallen också detsamma:

 W₁ = W₂.

I alla fall upplever objektet en förändring i potentiell energi:

Förändring = slutlig potentiell energi - initial potentiell energi

Δu = u_slutlig - ELLER_första = U_B - ELLER_TILL

Tja, objektets potentiella energi definieras som det negativa av det arbete som utförts med våld (konservativ):

ΔU = -w_Ab

Men eftersom arbetet definieras av denna integral:

Kan tjäna dig: de 31 typerna av kraft i fysik och deras egenskaper

Var F och dr (med djärv eller pil på) är respektive styrka och förskjutningsvektorer. Med detta i åtanke är förändringen i potentiell energi den negativa av denna integral:

För konservativa krafter som beskrivs beräknas integralen lätt. 

Observera att enheterna med potentiell energi är desamma som arbetet. I det internationella systemet om enheten är Joule, vilket är förkortat och motsvarande 1 Newton X Metro, av den engelska fysikern James Joule (1818-1889).

Andra enheter för energi inkluderar Ergio i CGS-systemet, Pound-Fork X Foot, BTU (Brittisk termisk enhet), kalorier och kilowatt-hora.

Låt oss se några speciella fall av hur man beräknar potentiell energi.

Beräkning av gravitationspotentialenergi

I närheten av jordens yta pekar tyngdkraften vertikalt ner och dess storlek ges av ekvationen Vikt = massa x tyngdkraft.

Betecknar den vertikala axeln med bokstaven "Y" och tilldelar den här adressen enhetsvektorn J, positiv och negativ ner, förändringen i potentiell energi när en kropp rör sig från y = y_TILL fram tills y = y_B är:

Var m representerar kroppens kropp och g Värdet på tyngdkraften. Om du är vald och_TILL = 0 som referensnivå på marken, där du är fixerad som 0, har du:

U (y) = mgy

Beräkning av elastisk potentiell energi

Hookes lag säger att kraften är proportionell mot deformation:

F = -k.x

Här x Det är deformationen och k Det är en konstant på våren, vilket indikerar hur styv det är. Genom detta uttryck beräknas elastisk potentiell energi med hänsyn till det Yo Det är enhetsvektorn i horisontell riktning:

När du väljer ELLER_TILL = 0 i  x_TILL, Det föregående uttrycket är funktionen U (x) För vårens potentiella energi:

U (x) = ½ kx²

Elektrostatisk potentiell energiberäkning

När du har en punktlig elektrisk laddning producerar den ett elektriskt fält som uppfattar en annan punktlig belastning q, Och vad fungerar det när man flyttar från en position till en annan mitt i fältet. Den elektrostatiska kraften mellan två specifika belastningar har radiell riktning, symboliserad genom enhetsvektorn r:

 Här k_och Det är den elektrostatiska eller konstant konstanten av Coulomb, vars värde är k_och ≈ 9 x 10⁹  N.m² /C² I internationella systemenheter. Det följer att:

 Välja u = 0 när r_TILL → ∞, kvarstår:

Löst övningar

- Övning 1: En vår som sträcker sig

En fjäder vars konstant är k = 10.0 n/cm sträcker sig initialt 1.00 cm från dess jämviktslängd. Det uppmanas att beräkna den extra energi som krävs för att sträcka våren upp till 5.00 cm utöver dess jämviktslängd.

Lösning 

Ersätter direkt x = 1.00 cm i ekvationen för u (x).CM, men centimeter måste bli meter för att få energi i Joules:

U (1) = 0.5 x 10.0 n/cm x (1.00 cm)² = 5 n. cm = 0.05 J; U (5) = 0.5 x 10.0 n/cm x (5.00 cm)² = 125 n.cm = 1.25 J

Därför är skillnaden i energi som söks 1.25 - 0.05 J = 1.20 j.

- Övning 2: Konservativa och icke -konservativa krafter

Ett litet block från punkt A släpps från vila, så att den glider längs den böjda rampen utan friktion till punkt B. Därifrån kommer den in i en lång grov horisontell yta, med en dynamisk friktionskoefficient μ_k = 0.2. Hitta på vilket avstånd från punkt B stannar, förutsatt att h_TILL= 3m.

Kan tjäna dig: Barrada spiral galax: bildning, evolution, egenskaper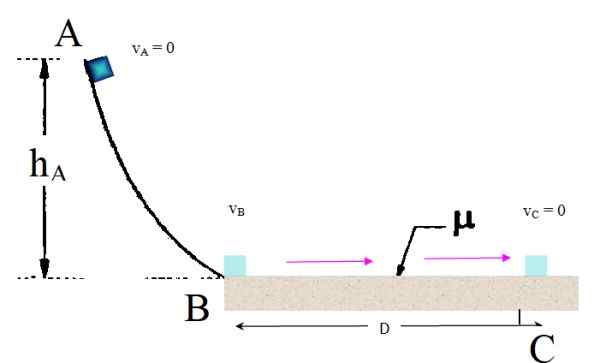Figur till exempel 1. Källa: f. Zapata.

Lösning 

När blocket är i en höjd h_TILL När det gäller golvet har den gravitationspotential energi på grund av dess höjd. När den släpps blir denna potentiella energi gradvis kinetisk energi, och när den glider genom den släta böjda rampen ökar hastigheten.

Under resan från A till B kan inte ekvationerna för den enhetligt varierade rektilinära rörelsen tillämpas. Medan tyngdkraften är ansvarig för rörelsen av blocket, är rörelsen att denna upplever är mer komplex, eftersom banan inte är rätlinjig.

Energibesparing på AB -rutten

Men eftersom tyngdkraften är en konservativ kraft och i rampen finns det ingen friktion, bevarande av mekanisk energi kan användas för att hitta hastigheten när den når slutet av rampen:

Mekanisk energi vid A = mekanisk energi i B

m.g.h_TILL + ½ m.v_TILL² = m.g.h_B + ½ m.v_B²

Uttrycket förenklas genom att märka att massan visas i varje termin. Släpps från vila v_TILL = 0. Och h_B Det är på marknivå, h_B = 0. Med dessa förenklingar reduceras uttrycket till:

v_B² = GH_TILL

Arbete utförd genom att gnugga i avsnitt BC

Nu börjar blocket sin rutt i det grova avsnittet med denna hastighet och slutar slutligen vid punkt C. Därför v_C = 0. Mekanisk energi bevaras inte längre, eftersom friktion är en dissipativ kraft, som har gjort ett jobb på blocket som ges av:

W_Rör = -Frue of Friction X Distance reste

Detta arbete har ett negativt tecken, eftersom kinetisk friktion bromsar ner till objektet och motsätter sig dess rörelse. Storleken på kinetisk friktion F_k  är:

F_k = μ_k .N

Där n är storleken på normal kraft. Den normala kraften utövas av ytan på blocket, och eftersom ytan är helt horisontell, eftersom den balanserar vikten P = mg, Därför är det normala storleken:

N = mg

Vad leder till:

F_k = μ_k .mg

Arbetet som F_k Gör på blocket är: W_k = - f_k .D =- μ_k .mg.D.

Beräkning av förändring i mekanisk energi

Detta arbete motsvarar förändringen i mekanisk energi, beräknat så här:

Mekanisk energi i C - Mekanisk energi vid B =

Δe_m = (U_C +K_C)- (eller_B + K_B) = - μ_k .mg.D

I denna ekvation finns det några termer som upphävs: k_C = 0, eftersom blocket stannar i C och också är ogiltig_C = U_B, för att vara dessa punkter på marknivå. Förenkling resulterar i:

- K_B = - μ_k .m.g.D

½ m.v_B² = μ_k .m.g.D

Degen avbryts igen och kan erhållas enligt följande:

D = (½ v_B²)/(μ_k . G) = (½ v_B²)/(μ_k . g) = (½g.h_TILL)/(μ_k . g) = (½h_TILL)/μ_k = 0.5 x 3 m / 0.2 = 7.5 m

Referenser

1. Bauer, w. 2011. Fysik för teknik och vetenskap. Volym 1. MC Graw Hill.
2. Figueroa, D. (2005). Serie: Physics for Science and Engineering. Volym 2. Dynamisk. Redigerad av Douglas Figueroa (USB).
3. Giancoli, D.  2006. Fysik: Principer med applikationer. Sjätte. Ed Prentice Hall.
4. Riddare, r.  2017. Fysik för forskare och teknik: En strategistrategi. Pearson. 
5. Sears, Zemansky. 2016. Universitetsfysik med modern fysik. 14th. Ed. Volym 1-2.