Skär ansträngningen hur det beräknas och lösta övningar

Det är känt som ren styrka vilket är resultatet av att applicera två krafter parallellt med ett område och i motsatt riktning. På detta sätt kan ett objekt delas upp i två delar, vilket gör att sektionerna glider över varandra.

Dagliga direktskärningar på tyger, papper eller metaller, utövade av sax, guillotiner eller skjuvning. De visas också i strukturer som bultar eller skruvar, stift, balkar, kilar och svetsar.

Figur 1. Med en sax görs en skjuvningsinsats. Källa: Pixabay

Det är nödvändigt att klargöra att det inte alltid är avsett att sektionera eller klippa, men skjuvansträngningen tenderar att deformera objektet som det tillämpas på; Det är därför de strålar som utsätts för skärningsinsatser tenderar att kombinera med sin egen vikt. Följande exempel klargör poängen.

Figur 2 visar ett enkelt schema för att illustrera ovanstående. Det är ett objekt som två krafter agerar i motsatta riktningar. Det finns ett imaginärt skärplan (det är inte ritat) och krafterna verkar på varje sida av planet och skär i två stången.

När det gäller en sax: varje ark eller kant tillämpar en kraft på korsets (cirkulära) avsnitt av objektet som ska klippas, så att det också separeras i två delar, såsom strängen i figur 1.

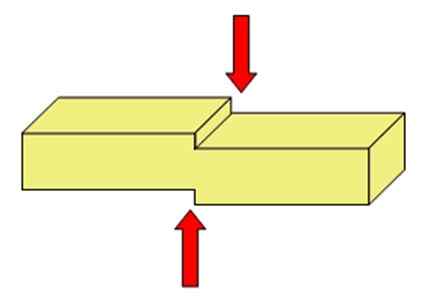figur 2. De två visade krafterna utövar en ansträngning som tenderar att dela stången i två. Källa: ADRE-ES [CC BY-SA 4.0 (https: // CreativeCommons.Org/licenser/BY-SA/4.0)] [TOC]

Skärinsats kan orsaka deformation

Du kan försöka utöva en skjuvinsats genom att skjuta handen på locket till en stängd bok. Det andra locket måste förbli fixerat på bordet, som kan uppnås genom att stödja den fria handen så att det inte rör sig. Boken kommer att deformeras lite med denna åtgärd, som schematiserad i följande figur:

Figur 3. När du tillämpar en skjuvinsats på boken finns en deformation. Källa: Krishnavedala [CC0]

Om denna situation analyseras noggrant, tillämpas de två krafterna som redan hänvisas till, men den här gången tillämpades horisontellt (I Fuchsia). Den ena är den av hans hand på det ena ansiktet och den andra appliceras av ytan på bordet på motsatt ansikte av boken som är fixerad.

Kan tjäna dig: tröghet

Boken vänder sig inte, även om dessa krafter kan orsaka ett vridmoment eller ett nettomoment. För att undvika detta är de andra två vertikala krafterna (i turkos); Den som applicerades med den andra handen och den normala som utövades vid bordet, vars nettomoment verkar i motsatt riktning förhindrar rotationsrörelsen.

[TOC]

Hur beräknas skjuvansträngningen?

Skärningsinsatser förekommer även inuti människokroppen, eftersom blodet när cirkulärt kontinuerligt utövar tangentiella krafter på blodkärlennas inre ansikte, vilket orsakar små deformationer i väggarna.

Dess övervägande är viktigt för att bestämma möjligheterna för att misslyckas med att misslyckas. Vid skärande ansträngningar beaktas inte bara styrkan utan också det område som det verkar.

Detta förstås omedelbart när man tar två cylindriska staplar av samma längd, gjorda med samma material men av olika tjocklek och utsätter dem för att öka ansträngningarna tills de går sönder.

Uppenbarligen kommer de nödvändiga krafterna att vara mycket olika, eftersom en stapel är tunnare än den andra; Ansträngningen kommer dock att vara densamma.

Skjuvansträngningen betecknas med de grekiska texterna τ (tau) och beräknas som förhållandet mellan storleken på den applicerade kraften F och området TILL av ytan som den verkar på:

τ_genomsnitt= F /a

Den således beräknade ansträngningen är den som producerar en genomsnittlig kraft på den aktuella ytan, eftersom kraften inte verkar på en unik punkt på ytan, utan distribueras över allt och inte på ett enhetligt sätt. Distributionen kan dock representeras av en resulterande kraft som verkar på en viss punkt.

Det kan tjäna dig: Block Algebra: Elements, Exempel, Löst övningar

Dimensionerna på skjuvspänningen är av kraft på ytan. I enheter av det internationella systemet motsvarar Newton/Metro Square, enhet som heter Pascal och förkortat PA.

De är samma tryckenheter, därför enheterna i det engelska systemet som pund -fuerza/pie ² och Vågen-fuerza /tum² De är också lämpliga.

Skärning och deformation

I många situationer är storleken på skjuvspänningen proportionell mot den enhetliga deformationen som orsakas i objektet, till exempel boken i föregående exempel, som kommer att återgå till dess ursprungliga dimensioner så snart handen tas bort. Isåfall:

Ren styrka ∝ Enhet deformation

Proportionalitetskonstanten i detta fall är skärmodulen, styvhetsmodulen eller skjuvmodulen (g):

Skärinsats = Hörmodul X -enhetsdeformation

τ = g. y

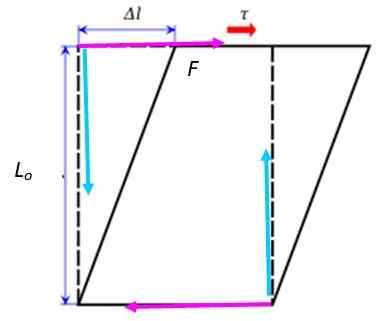
Med y = 5L/l_antingen, Där ΔL Det är skillnaden mellan den slutliga längden och den initiala. Genom att kombinera de givna ekvationerna kan ett uttryck för deformation som orsakas av ansträngningen hittas:

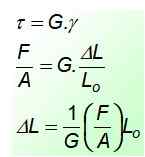
Konstantens värde G Det finns i tabellerna och dess enheter är desamma som de för ansträngningen, med tanke på att enhetsdeformationen är dimensionlös. Nästan alltid värdet på G är en halv eller tredjedel av värdet av OCH, Elasticitetsmodulen.

De är faktiskt relaterade till uttryck:

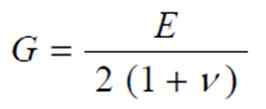
Där v är Poisson -modulen, en annan elastisk konstant av materialet vars värde är mellan 0 och ½. Det är därför g i sin tur är mellan E/3 och E/2.

Löst övningar

-Övning 1

För att gå med i två järnplattor används en stålskruv, som måste motstå skärkrafter på upp till 3200 n. Vad är minimidiametern på skruven om säkerhetsfaktorn är 6.0? Det är känt att materialet motstår upp till 170 x 10⁶ N/m².

Kan tjäna dig: vit dvärg

Lösning

Den skärningsansträngande som skruven utsätts för kommer från de krafter som visas i figuren nedan. Säkerhetsfaktorn är en måttlös mängd och är relaterad till den maximala tillåtna ansträngningen:

Skärinsats = f/a = maximal tillåten ansträngning/säkerhetsfaktor

Därför är området:

A = F X Säkerhetsfaktor / skärning = 3200 x 6/170 x 10⁶ = 0.000113 m²

Skruvområdet ges av πd²/4, därför är diametern:

D²= 4 x a/π = 0.000144 m²

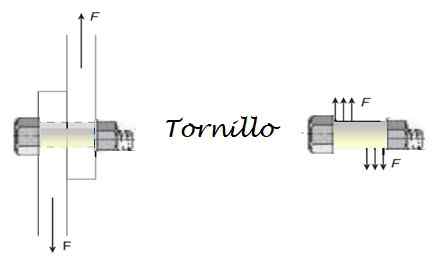Figur 4. Skär ansträngning på skruven. Källa: Självgjord.

D = 0.012 m = 12 mm.

-Övning 2

En trästift eller taco används för att förhindra att remskivans vändning utsätts för spänningar T₁ och T₂, När det gäller en 3 -tums axel. Stiftdimensionerna visas i figuren. Hitta storleken på skjuvspänningen på taco, om de visade krafterna verkar på remskivan:

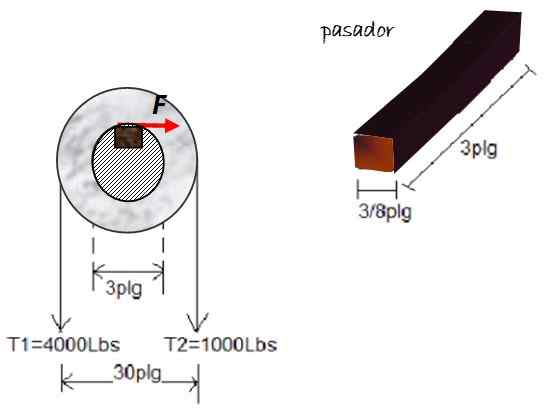Figur 5. Gratis kroppsdiagram till exempel 2. Källa: Självgjord.

Lösning

T₁ producerar ett vridmoment i en antihorarium -mening på remskivan, som tilldelas positivt tecken, medan T₂ Producerar vridmoment i ett schema med ett negativt tecken. Den 15 -tums spakarmen för varje spänning. Därför:

Nettovridmoment = 4000 pund-kraft . 15 tum - 1000 pund -kraft. 15 tum = 45000 pund-kraft . tum

Trätacon ska inte vända, då måste stunderna med avseende på tacoens centrum vara noll. F representerar medelkraften på ytan:

Fyra fem.000 - f.D = 0

Med D = 1.5 tum, därför:

F x 1.5 = 45.000

F = 30.000 pund kraft

Denna kraft orsakar en skarp storleksarbete:

τ = f/a = 30.000 pund-fuerza / (3/8 x 3) tum² = 2.67 x 10⁴ Libras-fuerza/tumga²

Referenser

1. Öl, f. 2010. Materialmekanik. Femte. Utgåva. McGraw Hill. 7 - 9.
2. Fitzgerald, 1996. Materialmekanik. Alfa -omega. 21-23.
3. Giancoli, D.  2006. Fysik: Principer med applikationer. 6^th  Ed. Prentice hall. 238-242.
4. Hibbeler, R.C. 2006. Materialmekanik. Sjätte. Utgåva. Pearson Education. 22 -25
5. Valera Negrete, J. 2005. Allmänna fysikanteckningar. Unk. 87-98.
6. Wikipedia. Skjuvspänning. Återhämtad från: in.Wikipedia.org.