Vanlig faktor för grupperingsvillkor, övningar

han Vanlig faktor för grupperingsvillkor Det är en algebraisk procedur som tillåter att skriva några algebraiska uttryck i form av faktorer. För att uppnå detta mål måste uttrycket först vara bekvämt gruppering och observera att varje grupp som sålunda bildats har i själva verket en gemensam faktor.

Att tillämpa tekniken kräver korrekt viss övning, men på kort tid är det möjligt att dominera. Låt oss först se ett illustrativt exempel som beskrivs steg för steg. Då kan läsaren tillämpa det de lärde sig i var och en av de övningar som kommer att dyka upp.

Figur 1. Ta bort gemensam faktor för gruppering av termer underlättar arbete med algebraiska uttryck. Källa: Pixabay.

Anta till exempel att du måste faktorera följande uttryck:

2x² + 2xy - 3zx - 3zy

Detta algebraiska uttryck består av 4 monomialer eller termer, separerade med tecken + och -, nämligen:

2x², 2xy, -3zx, -3zy

Observera noggrant, X är gemensamt för de första tre, men inte för det sista, medan och är gemensamt för den andra och den fjärde, och Z är gemensamt för den tredje och den fjärde.

Så i princip finns det ingen gemensam faktor för de fyra termerna samtidigt, men om de grupperas som det kommer att visas i följande avsnitt kan man hjälpa till att skriva uttrycket som produkten av två eller flera faktorer.

[TOC]

Exempel

Faktor uttrycket: 2x² + 2xy - 3zx - 3zy

Steg 1: Grupp

2x² + 2xy - 3zx - 3zy = (2x² + 2xy) + (-3zx - 3zy)

Steg 2: Ta bort den gemensamma faktorn från varje grupp

2x² + 2xy - 3zx - 3zy =

= (2x² + 2xy) - (3zx + 3zy) =

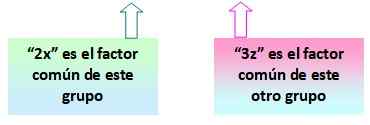
= 2x (x+y) - 3z (x+y)

YoMportant: Det negativa tecknet är också en vanlig faktor som måste beaktas.

Kan tjäna dig: Vector Space: Base and Dimension, Axioms, Egenskaper

Lägg nu märke till att parentesen (x+y) upprepas i de två termerna som erhålls vid gruppering. Det är den vanliga faktorn som letade efter.

Steg 3: Faktorisera allt uttryck

2x² + 2xy - 3zx - 3zy = (x+y) (2x - 3z)

Med det föregående resultatet har målet med faktoriseringen uppnåtts, vilket är ingen annan än att omvandla ett algebraiskt uttryck baserat på summor och subtraktion av termer, i produkten av två eller flera faktorer, i vårt exempel, av: (x+ y) och (2x - 3z).

Viktiga frågor om den gemensamma gruppfaktorn

Fråga 1: Hur man vet att resultatet är korrekt?

Svar: Distributivegenskap tillämpas på det erhållna resultatet och efter att ha minskat och förenklat måste uttrycket således uppnås sammanfalla med det ursprungliga, om inte, det finns ett fel.

I föregående exempel fungerar det omvänt med resultatet för att verifiera att det är bra:

(x+y) (2x - 3z) = 2x² -3ZX +2xy - 3zy

Eftersom tilläggsordningen inte ändrar summan, efter att ha tillämpat den distribuerande egenskapen, alla originalvillkoren, finns det tecken, därför är faktoriseringen korrekt.

Fråga 2: Kunde du ha grupperat på ett annat sätt?

Svar: Det finns algebraiska uttryck som medger mer än en form av gruppering och andra som inte gör det. I det valda exemplet kan läsaren prova andra möjligheter, till exempel gruppering:

2x² + 2xy - 3zx - 3zy = (2x²- 3ZX) + (2xy - 3zy)

Och du kan se att resultatet är detsamma som erhålls här. Att hitta den optimala gruppen är en fråga om praxis.

Kan tjäna dig: Cotangent härledd: beräkning, demonstration, övningar

Fråga 3: Varför är det nödvändigt att få gemensam faktor från ett algebraiskt uttryck?

Svar: Eftersom det finns tillämpningar där det faktoriserade uttrycket underlättar beräkningar. Anta till exempel att du vill göra 2x² + 2xy - 3zx - 3zy lika med 0. Vad skulle vara möjligheterna?

För att svara på detta problem är den faktoriserade versionen mycket mer användbar än den ursprungliga utvecklingen i termer. Det uppstår så här:

(x+y) (2x - 3z) = 0

En möjlighet att uttrycket är värt 0 är att x = -y, oavsett värdet på z. Och den andra är att x = (3/2) z, utan att tänka på värdet på y.

Övningar

- Övning 1

Få gemensam faktor för följande uttryck genom att gruppera termer:

ax+ay+bx+av

Lösning

De två första är grupperade, med den gemensamma faktorn "A" och de två sista med den gemensamma faktorn "B":

AX+AY+BX+av = A (x+y)+b (x+y)

När detta är gjort avslöjas en ny vanlig faktor, som är (x+y), så att:

Ax+ay+bx+av = a (x+y)+b (x+y) = (x+y) (a+b)

Ett annat sätt att gruppera

Detta uttryck medger ett annat sätt att gruppera. Låt oss se vad som händer om termerna omorganiseras och en grupp är gjord som de innehåller X och en annan med de som innehåller och:

ax +ay +bx +av = ax +bx +ay +av = x (a +b) +y (a +b)

På detta sätt är den nya gemensamma faktorn (A+B):

ax+ay+bx+av = ax+bx+ay+av = x (a+b)+y (a+b) = (x+y) (a+b)

Det leder till samma resultat av det första sättet att gruppera att det testades.

- Övning 2

Det krävs att skriva följande algebraiska uttryck som de två faktorprodukten:

3: e³ - 3: e²B+9AB²-till²+AB-3B²

Kan tjäna dig: Coplanares Points: Ekvation, exempel och lösta övningar

Lösning

Detta uttryck innehåller 6 termer. Låt oss försöka gruppera första och fjärde, andra och tredje och slutligen femte och sjätte:

3: e³ - 3: e²B+9AB²-till²+AB-3B² = (3: e³ -till²) + (- 3: e²B+9AB²) + (AB-3B²)

Nu är varje parentes faktor:

= (3: e³ -till²) + (- 3: e²B+9AB²) + (AB -3B²) = a² (3A -1) + 3AB (3B -A) + B (A -3B)

Vid första anblicken verkar det som om situationen har varit komplicerad, men läsaren bör inte avskräckas, eftersom vi kommer att skriva om den sista terminen:

till² (3A -1) + 3AB (3B -A) + B (A -3B) = A² (3A - 1) + 3AB (3B -A) - B (3B -A)

De sista två termerna har nu en gemensam faktor, som är (3B-A), så att de kan faktoriseras. Det är mycket viktigt att inte tappa den första terminen till den första terminen² (3A - 1), som måste fortsätta att följa allt som att lägga till, så att du inte arbetar med honom:

till² (3A - 1) + 3AB (3B -A) - B (3B -A) = A² (3A-1) + (3B-A) (3AB-B)

Uttrycket har reducerats till två termer och en ny vanlig faktor upptäcks i det sista, vilket är "B". Nu kvarstår det:

till² (3A-1) + (3B-A) (3AB-B) = A² (3A-1) +B (3B-A) (3A-1)

Den nästa gemensamma faktorn för att dyka upp är 3: e - 1:

till² (3A - 1) +B (3B -A) (3A -1) = (3A - 1) [a² + B (3b-a)]

Eller om du föredrar utan fyrkantiga konsoler:

(3: e - 1) [a² + B (3B -A)] = (3A - 1) (a² -AB + 3B²)

Kan läsaren hitta ett annat sätt att gruppera som leder till samma resultat?

figur 2. Föreslagna faktoriseringsövningar. Källa: f. Zapata.

Referenser

1. Baldor, a. 1974. Elementär algebra. Venezuelan kultur.TILL.
2. Jiménez, r. 2008. Algebra. Prentice hall.
3. Huvudfall av faktorisering. Återhämtat sig från: julioprofe.netto.
4. Unk. Grundläggande matematik: Faktorisering genom att gruppera termer. Redovisningsfakultet.
5. Zill, D. 1984. Algebra och trigonometri. Macgraw Hill.