Förpackningsfaktor

Förpackningsfaktorn är en bråkdel som indikerar hur mycket volym partiklarna upptar, vare sig atomer, joner eller molekyler, i det inre utrymmet i en kristall. Dess värde är alltid mindre än 1, vilket blir 100% av glasets volym; Mer exakt, dess enhetliga cell, som är den minsta representationen av hela glaset.

En 100% förpackningsfaktor innebär att partiklarna upptar volymen på den enhetliga cellen i sin helhet. Fysiskt är det omöjligt för detta att hända, eftersom det till exempel skulle innebära att atomerna deformerar deras radioapparater och löses upp som om de var en "elektronisk vätska". Atomernas geometri, sfärisk för bekvämlighet, resulterar alltid i tomma utrymmen under förpackningen.

Eftersom det händer i söta dispenseringsmaskiner berättar förpackningsfaktorn hur "snäva" är partiklarna i en kristall: ju större det är, desto mer gummi eller atomer kommer det att finnas i rymden

I definitionen av förpackningsfaktorn antas att atomerna består av styva sfärer, såsom gummi eller godisbollar av en dispenserad maskin (överlägsen bild). Bland sfärerna kommer det alltid att finnas ihåliga utrymmen där mindre sfärer (föroreningar eller tillsatser kan smygas).

Om vi ​​ökar förpackningsfaktorn kommer sfärerna att pressas och vrida det mest kompakta och täta glaset; eller å andra sidan, mer deformerbar, som med formbara och duktila metaller.

Förpackningsfaktorn gäller för alla typer av glas. Emellertid kan beräkningen bli lite tråkig, så den kommer bara att övervägas för atomkristaller med enkla strukturer.

[TOC]

Förpackningsfaktorformel

Förpackningsfaktorn uttrycks vanligtvis som procentsatser. Till exempel, om dess värde är 40%, betyder det att partiklarna knappt upptar 40% av det totala utrymmet för enhetscellen; eller vad som är detsamma som att säga att 60% av glaset är "tomt".

Ovanstående klargör vad som är formeln för att beräkna denna faktor:

• Ful = (volym atomer)/ (enhetscellvolym)

Där ful betyder Atomförpackningsfaktor, Vilka är de enklaste kristallerna.

Volymen på enhetscellen beror på dess parametrar (till exempel längden på dess sidor), med vilken den fortsätter med enkel geometri för att beräkna dess volym. Atomerna är å andra sidan de som definierar cellen, så det är möjligt att uttrycka dimensionerna på samma från atomradioerna, vilket kommer att ses i nästa avsnitt.

Det kan tjäna dig: Racemic Mix: Chirality, Exempel

När det gäller volymen av atomer är det totala antalet av dem som finns i enhetscellen (1, 2, 3, etc.), liksom dess sfäriska geometri. Därför modifieras formeln lite:

Ugly = (nº atomer) (atomvolym)/ (enhetscellvolym)

För att beräkna ful måste du bestämma då Nej, v_atom och v_Enhetscell.

Enkel kubik

Enkel kubikenhetscell. Källa: ccc_crystal_cell_ (ogenomskinlig).Svg: *cobique_centre_atomes_par_maille.SVG: CDANG (Original Idea och SVG Execution), Samuel Dupré (3D odeeling med Solidworks) härleder arbete: Daniele Pugliesi (Talk) Derivera arbete: Daniele Pugliesi, CC BY-SA 3.0, via Wikimedia Commons

Den enklaste enhetscellen av allt är den enkla kubiken. I den har vi några delar av atomerna i vart och ett av hörnen. Om vi ​​ser kommer vi att märka att längden till Från denna cell är den lika med 2R, eftersom det är atomerna som definierar cellen. Så, volymen på enhetscellen kommer att vara lika med:

V_Enhetscell = till³ (Volym av en kub)

= (2r)³

= 8r³

Samtidigt kommer atomens volym att vara lika med:

V_atom = (4/3) πr³ (Volym av en sfär)

Var och en av hörnen delas av ytterligare 8 angränsande enhetsceller. Därför har vi en 1/8 fraktion i varje hörn, och med 8 av dem bryr vi oss inte 1 atom per enhetscell (1/8 x 8 = 1).

Förpackningsfaktorn är:

Ful = (1) (4/3) πr³ /8r³

= π/6 ≈ 52%

Det vill säga i en enkel kubikcell upptar atomerna 52% av hela glasvolymen.

Kubikcentrerad i kroppen

Bestämning av cellvolymen

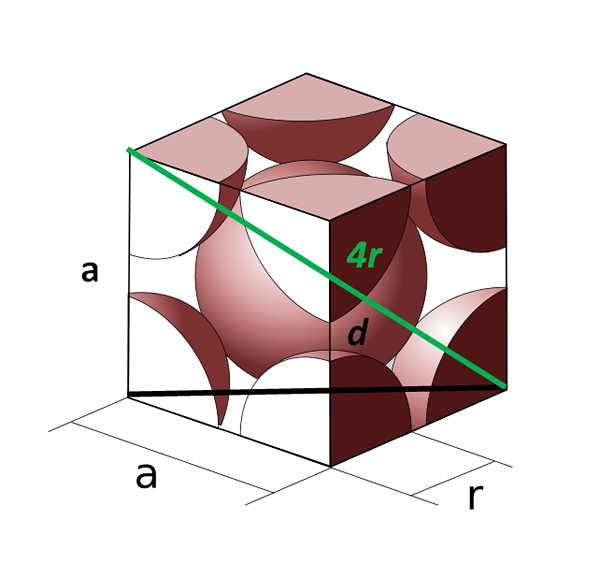Kroppens enhetscell centrerad på kroppen. Källa: cobique_centre_atomes_par_maille.SVG: CDANG (originalidé och SVG-exekvering), Samuel Dupré (3D odeeling med Solidworks) derivatarbete: Daniele Pugliesi, CC BY-SA 3.0, via Wikimedia Commons

Låt oss nu se kubikcellen centrerad på kroppen. Sidan till Det kan inte längre vara lika med 2R, eftersom vi har ett tomt utrymme mellan de två atomerna i hörnen. Det finns därför en diagonal d lika med 4R (grön färg) som korsar cellen genom mitten och rör vid motsatta hörn, och en annan diagonal d av ansiktet (svart).

Sidorna till, d och 4R ritar en rektangel triangel till vilken vi kan tillämpa trigonometri för att beräkna vad som är värdet på till:

(4R)² = D² + till²

Kan tjäna dig: Intermolekylära krafter

Men å andra sidan har vi vid basen av enhetscellen en annan triangel (till, till och d) som vi kan beräkna hypotenusen:

d²  = a² + till²

= 2a²

Ersätter vi då:

(4R)² = (2: a²) + a²

(4R)² = 3A²

A = (4/√3) r

V_Enhetscell är lika med:

V_Enhetscell = a³

= ((4/√3) r)³

Bestämning av förpackningsfaktorn

Observera att med avseende på antalet atomer har vi en atom i denna cell, efter samma avdrag som gjorts för den enkla kubikcellen, och en annan ytterligare atom som ligger i mitten av cellen. Således finns det totalt 2 atomer för varje kubikcell som är centrerad på kroppen.

Förpackningsfaktorn är då:

Ful = (2) (4/3) πr³ / ((4/ √3) r)³

= (√3/8) π ≈ 68%

Det vill säga, i en kubikcell som är inriktad på kroppen är 68% av glasvolymen ockuperad av atomer. Följaktligen är detta kristallina arrangemang mer kompakt (eller tät) än den enkla kubiken.

Kubikcentrerad ansikten

Bestämning av cellvolymen

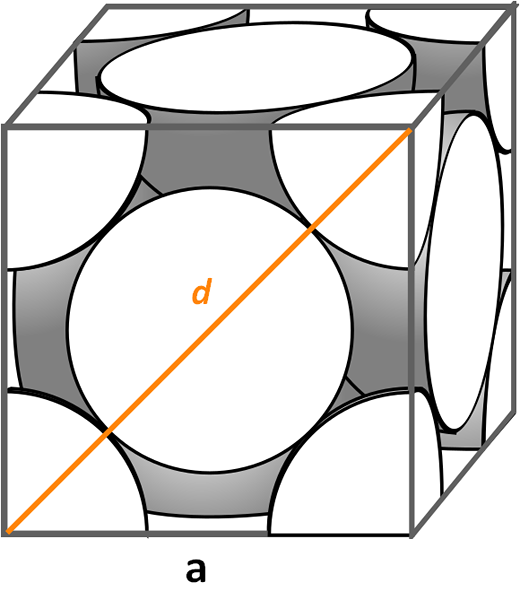Kubisk enhetscell centrerad på ansikten. Källa: CDANG, CC BY-SA 3.0, via Wikimedia Commons

Låt oss titta på den kubiska enhetscellen centrerad på ansikten, mycket vanligt i symfiner av oorganiska salter och vissa metaller, som guld och silver. För att bestämma sin förpackningsfaktor måste vi starta, efter de tidigare exemplen, för att hitta vad volymen på sin enhetscell är. Det är nödvändigt att beräkna sidan igen till Och så volymen på kuben till³.

Den här gången är proceduren enklare och mer direkt, eftersom vi har en diagonal d Fram det tillsammans med sidorna till, De bildar en höger triangel som vi kan tillämpa trigonometri:

d² = a² + till²

= 2a²

Clearing till vi kommer att ha:

till = D/√2

Men vi märker visuellt det d Det är lika med 4R, så vi gör en substitution:

till = 4r/√2

= 2r 2^1-1/2

= (2√2) r

Vara v_Enhetscell lika med:

till³ = ((2√2) r)³

= (16√2) r³

När det gäller antalet atomer per cell har vi åtta delar av en atom i varje hörn, och även en halv atom för vart och ett av de sex ansikten, som delas av en annan angränsande cell. Därför är antalet atomer lika med:

Nº atomer = 1/8 (8) + 1/2 (6) = 1 + 3 = 4

Bestämning av förpackningsfaktorn

Med att det finns fyra atomer i varje kubikcell som är inriktad på ansikten, och även dess volym, vilket är lika med (16√2) r³, Vi kan sedan beräkna förpackningsfaktorn:

Ugly = (nº atomer) (atomvolym)/ (enhetscellvolym)

= (4) (4/3) πr³ / (16√2) r³

Det kan tjäna dig: Acilo Group: Struktur, egenskaper, föreningar och derivat

= π/(3√2) ≈ 74%

Observera att denna cell är ännu mer kompakt än de tidigare: 74% av den totala volymen av cellen ockuperas av atomer. I en perfekt och ren kristall skulle detta motsvara att 26% av dess volym är tillgängliga för att vara värd för andra gästatomer.

Kompakt hexagonal

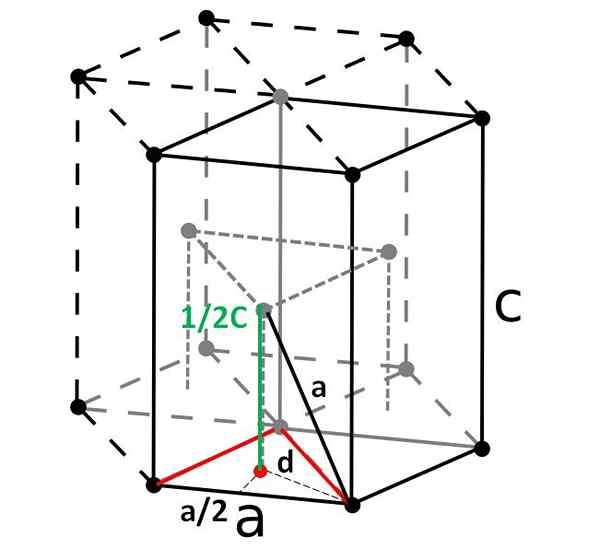Kompakt hexagonal cell och dess rhombohedral primitiv cell. Källa: Original: Dornelfvector: Depiep, CC BY-SA 3.0, via Wikimedia Commons

Slutligen, bland de enklaste och mest kompakta enhetscellerna har vi den kompakta sexkantiga. Till skillnad från de tidigare är beräkningen av dess volym lite mer besvärlig. Som man kan se är det inte kubiskt, så det har två parametrar till och c, Det senare är cellens höjd.

Bestämning av cellens höjd

Den hexagonala cellen kan delas upp i tre romboyanska celler, och från en av dem kommer den att beräknas till och c. Sidan till, Även om det inte är så tydligt i bilden ovan, är den lika med 2R. Att beräkna c, Istället använder vi triangeln och den röda punktprodukten av det inre triangulära prismen i samma cell.

Vi måste beräkna avståndet d Att kunna avgöra hur mycket det är värt c. På golvet är den röda triangeln liksidig, med en vinkel på 60º. Men om en annan intern rektangel triangel betraktas med sidor till/2 och d, och en vinkel på 30 ° (hälften), då kan vi genom trigonometri bestämma d:

Cos (30º) = (till/2) / d

d = till/√3

Och nu överväger vi rätt triangel som består av sidorna c/2 (grön), till (svart och d (prickad):

till² = (till/√3)² + (C/2)²

Clearing c Vi skulle ha:

c = √ (8/3) till

Och ersätter till Med 2r:

c = √ (8/3) (2R)

= √ (4 · 2/3) (2R)

= 4√ (2/3) r

Bestämning av cellvolymen

För att bestämma volymen på den hexagonala cellen måste du multiplicera hexagonområdet med dess höjd. Att veta att liksidiga trianglar har sidor till, Dess höjd beräknas h. Således hitta området för en triangel, vilket är för detta fall √3/4till², Vi multiplicerar detta värde med 6 för att få hexagonområdet: 3 (√3/2)till²

Volymen är därför:

V_Enhetscell = Hexagon Area X höjd

= 3 (√3/2)till² X 4√ (2/3) r

Och ersätta igen till Med 2r:

V_Enhetscell  = 3 (√3/2) (2R)² X 4√ (2/3) r

= 24√2 r³

Bestämning av förpackningsfaktorn

I den hexagonala cellen finns 12 atomer i hörnen, som har 1/6 av sina volymer inuti. Det finns också 3 inre atomer vars volymer är kompletta och ytterligare 2 atomer på de övre och nedre ansikten vars hälften av dess volymer är inne i cellen.

Därför är antalet atomer lika med:

Nº atom = 1/6 (12) + 1 (3) + 1/2 (2) = 6 atomer

Och förpackningsfaktorn är äntligen:

Ugly = (nº atomer) (atomvolym)/ (enhetscellvolym)

= (6) (4/3) πr³ / 24√2 r³

= π/(3√2) ≈ 74%

Observera att fackfaktorn för den hexagonala cellen är densamma som för kubikcellen centrerad på ansikten. Det vill säga båda är lika kompakta.

Referenser

1. C. Barry Carter & M. Grant Norton. (2007). Keramiska materialvetenskap och teknik. Kandare.
2. Shiver & Atkins. (2008). Oorganisk kemi. (Fjärde upplagan). MC Graw Hill.
3. Whitten, Davis, Peck & Stanley. (2008). Kemi. (8: e upplagan.). Cengage Learning.
4. Wikipedia. (2021). Atomförpackningsfaktor. Hämtad från: i.Wikipedia.org
5. Brandon. (2021). Vad är atomförpackningsfaktor (och hur man beräknar den för SC, BCC, FCC och HCP)? Material Science & Engineering Student. Återhämtad från: msestudent.com