Viskös friktion (kraft) koefficient och exempel

De viskös friktion Det uppstår när ett fast föremål rör sig i mitten av en vätska -un -gas eller en vätska-. Det kan modelleras som en kraft som är proportionell mot den negativa av objektets eller fyrkantens hastighet.

Användningen av en eller annan modell beror på vissa förhållanden, till exempel den typ av vätska där objektet flyttas och huruvida det är väldigt snabbt eller inte. Den första modellen är känd som Linjärt motstånd, och i den storleken på viskös friktion f_Rör Det ges av:

F_Rör = Γv

Figur 1. Paracharidister upplever viskös kraft under sin härkomst, eftersom luften erbjuder motstånd. Källa: Pixabay.

Här är γ konstanten för proportionalitet eller koefficient för viskös friktion och V är objektets snabbhet. Det är tillämpligt på kroppar som rör sig med låga vätskor med laminär regim.

I den andra modellen, känd som Kvadratisk motstånd O Rayleights lag, storleken på friktionskraften beräknas enligt:

F_Rör = ½ ρ.TILL.C_d.v²

Där ρ är vätskans densitet är A tvärsektionsarean för objektet och C_d Det är den aerodynamiska resistankoefficienten.

Produkten ½ ρ.TILL.C_d  Det är en konstant aerodynamik som kallas D, vars enheter är kg/m, därför:

F_Rör = DV²

Denna modell är mer lämplig när objektens hastighet är medelstor eller hög, eftersom rörelsen producerar turbulens eller virvlar i sin väg i vätskan.

En rörlig tennisboll och bilarna på motorvägen är exempel på föremål där denna modell fungerar ganska bra.

Viskoskraften uppstår eftersom det fasta ämnet måste ta vätskeskikten för att kunna röra sig genom den. Förekomsten av flera modeller beror på att denna kraft beror på flera faktorer, till exempel viskositeten hos vätskan, objektets hastighet och form.

Kan tjäna dig: vad är relativ permeabilitet?

Det finns fler aerodynamiska föremål än andra och många är utformade exakt så att mittens motstånd reducerar dess hastighet till ett minimum.

[TOC]

Exempel på viskosfriktion

Varje person eller föremål som rör sig i en vätska upplever nödvändigtvis motstånd från miljön, men många gånger föraktas dessa effekter för enkla applikationer som fritt fall.

I uttalanden om nästan alla fria fallproblem noteras det att effekterna av luftmotstånd föraktar sig själva. Detta beror på att luft är en ganska "tunn" vätska och det är därför vi hoppas att friktionen den erbjuder inte betydande.

Men det finns andra rörelser där viskös friktion har ett mer avgörande inflytande, låt oss se några exempel:

Stenar som faller i vatten och pollenkorn

-En sten som släpper vertikalt i ett rör fullt av oljeupplevelser en kraft som motsätter sig dess nedstigning, tack vare vätskemotstånd.

-Pollenkornen är mycket små, så för dem är luftens motstånd inte försumbar, för tack vare denna styrka lyckas de hålla sig flytande under lång tid, vilket orsakar säsongsallergier.

figur 2. Pollenkorn är tillräckligt små för att luftmotstånd har en betydande effekt. Källa: Pikrepo.

Simmare och cyklister

-När det gäller simmare använder de en hatt och de rakar sig helt så att vattenmotståndet inte drar hastigheten.

-Liksom simmare upplever cyklister i Counterreloj luftmotstånd, följaktligen har hjälmar aerodynamiska mönster för att förbättra effektiviteten.

Även cyklistens position inom en grupp i tävlingen är relevant. Den som leder marschen får uppenbarligen luftens största motstånd, medan för dem som stänger marschen är detta nästan noll.

Det kan tjäna dig: Andra jämviktstillstånd: Förklaring, exempel, övningar

Parakettare

-När en fallskärmshoppare öppnar fallskärmen utsätts den för den viskösa friktionen i luften, som är den mest lämpliga modellen som har hastighetens kvadrat. På detta sätt minskar det sin hastighet och när gnidningen är emot hösten når den ett konstant gränsvärde.

Bilar

-För bilar är den aerodynamiska motståndskoefficienten, en konstant som bestäms experimentellt och den yta som den presenterar mot vinden, de avgörande faktorerna för att minska luftmotståndet och minska konsumtionen. Det är därför de är designade med lutande vindrutor.

Millikans oljedroppsexperiment

-I Millikan Oil Drop -experimentet studerade fysiker Robert Millikan rörelsen av oljedroppar mitt i ett enhetligt elektriskt fält och drog slutsatsen att någon elektrisk laddning är flera av elektronbelastningen.

För detta var det nödvändigt att känna till dropparnas radie, som inte kunde bestämmas med direkt mått, med tanke på dess lilla storlek. Men i detta fall var den viskösa friktionen betydande och dropparna slutade bromsning. Detta faktum fick bestämma dropparnas radie och sedan dess elektriska laddning.

Övningar

- Övning 1

I ekvationen för viskös friktionskraft vid låg hastighet:

F_Rör = Γv

a) Vilka dimensioner om den viskösa friktionskoefficienten har y?

b) Vilka är y -enheterna i det internationella enhetssystemet?

Lösning till

Till skillnad från statiska eller kinetiska friktionskoefficienter har den viskösa friktionskoefficienten dimensioner, vilket måste vara:

Kan tjäna dig: fysisk vidhäftning: vad är och exempel

Styrka / hastighet

Kraften har dimensioner av massa x längd /tid², Medan hastigheterna är längd/tid. Genom att beteckna dem enligt följande:

-Massa: m

-Längd: L

-T

Måtten på den viskösa friktionskoefficienten γ är:

[M.L /t²] / [L / t] = [m.L.T / l.T²] = M/t

Lösning B

I SI är y -enheterna kg/s

- Övning 2

Med hänsyn till motståndet som vatten motsätter sig och hittar ett uttryck för terminalhastigheten för en metallfärit som faller vertikalt i ett rör fullt av olja, i fall:

a) Låg hastighet

b) hög hastighet

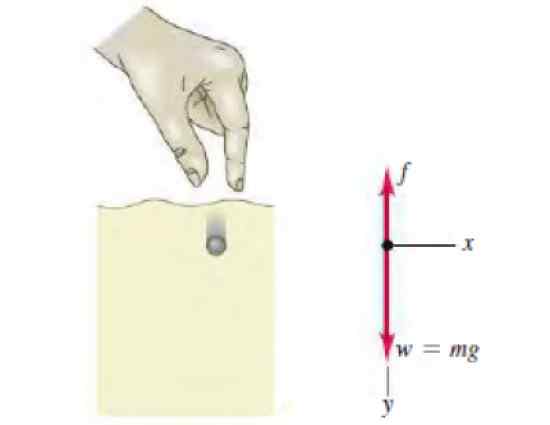Figur 3. Gratis kroppsdiagram över en sfärit som går ner i en vätska. Källa: Sears, Z. Universitetsfysik med modern fysik.

Lösning till

I figuren visas det fria kroppsdiagrammet och visar de två krafterna som verkar på sfäriten: vikten ner och vätskans motstånd, proportionellt mot hastigheten, uppåt. Newtons andra lag för denna rörelse fastställer följande:

γv_t - mg = 0

Där v_t Det är terminalhastigheten, som ges av:

v_t = mg / y

Lösning B

Om vi ​​antar genomsnitt i höga hastigheter är lämplig modell den med kvadrathastighet:

F_Rör = ½ ρ.TILL.C_d.v²

Så:

½ ρ.TILL.C_d.v² - mg = 0

D.v² - mg = 0

v = √ [mg / d]

I båda situationerna, ju större objektets massa, desto större är terminalhastigheten.

Referenser

1. Serway, R., Jewett, J. (2008). Fysik för vetenskap och teknik. Volym 1. 7th. Ed. Cengage Learning.
2. Sears, Zemansky. 2016. Universitetsfysik med modern fysik. 14th. Ed. Volym 1.
3. Tipler, s. (2006) Fysik för vetenskap och teknik. 5: e upplagan. Volym 1. Redaktör.
4. Tippens, s. 2011. Fysik: koncept och applikationer. Sjunde upplagan. McGraw Hill
5. Sevilla universitet. Friktionskrafter. Återhämtat sig från: Laplace.oss.är.