Konstant egenskapsfunktion, exempel, övningar

De konstant funktion Det är en där värdet på och. Med andra ord: En konstant funktion har alltid formen  f (x) = k, var k Det är ett riktigt nummer.

Genom att grafera konstantfunktionen i koordinatsystemet Xy, Det är alltid en rak linje parallell med den horisontella axeln eller axeln på x.

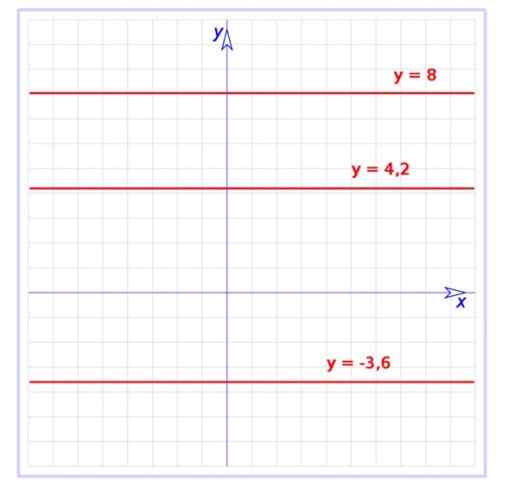
Figur 1. Graf över flera konstantfunktioner på det kartesiska planet. Källa: Wikimedia Commons. Användare: HITE [Public Domain]

Denna funktion är ett särskilt fall av besläktad funktion, vars graf är också en rak linje, men med sluttning. Konstantfunktionen har en icke -väntande, det vill säga det är en horisontell linje, som ses i figur 1.

Det finns grafen över tre konstantfunktioner:

f (x) = -3.6

G (x) = 4.2

H (x) = 8

Alla är raka parallella med den horisontella axeln, den första är under den axeln, medan de återstående är ovanför.

[TOC]

Konstantfunktionens egenskaper

Vi kan sammanfatta de viktigaste egenskaperna hos konstantfunktionen enligt följande:

-Dess graf är en horisontell rak linje.

-Den har unik korsning med axeln och, värde k.

-Det är kontinuerligt.

-Behärskningen av konstantfunktionen (uppsättningen värden som x) är uppsättningen av verkliga siffror R.

-Rutten, intervallet eller motsägelsen (uppsättningen värden som variabeln tar och) är helt enkelt konstanten k.

Exempel

Funktionerna är nödvändiga för att skapa kopplingar mellan storlekar som beror på varandra på något sätt. Det befintliga förhållandet mellan dem kan modelleras matematiskt för att veta hur den ena uppför sig när den andra varierar.

Kan tjäna dig: papomudas

Detta hjälper till att bygga modeller för många situationer och göra förutsägelser om deras beteende och utveckling.

Trots sin uppenbara enkelhet har den ständiga funktionen många tillämpningar. Till exempel när det gäller att studera storlekar som förblir konstant i tid, eller åtminstone, under en märkbar tid.

På detta sätt uppför sig storlekar i situationer som följande:

-De fart Kryssning av en bil som rör sig på en lång rätlinjär motorväg. Så länge den inte stannar eller accelererar, bär bilen en enhetlig rätlinjig rörelse.

figur 2. Om bilen inte stannar eller accelererar har den en enhetlig rätlinjig rörelse. Källa: Pixabay.

-En fulladdad och frånkopplad kondensor från en krets har en börda ständig i tid.

-Slutligen upprätthåller en parkeringsplats pris konstant oavsett hur länge en bil parkerade där.

Ett annat sätt att representera en konstant funktion

Konstantfunktionen kan växelvis representeras enligt följande:

f (x) = kx⁰

Sedan något värde på x Upphöjd till 0 ger 1 som ett resultat reduceras det tidigare uttrycket till det bekanta:

f (x) = k

Naturligtvis händer det så länge som värdet av k skiljer sig från 0.

Det är därför den ständiga funktionen också klassificeras som en polynomfunktion grad 0, sedan variabelns exponent x Det är 0.

Löst övningar

- Övning 1

Svara på följande frågor:

a) Kan det bekräftas att linjen som ges av x = 4 är en konstant funktion? Anledningen till ditt svar.

b) Kan en konstant funktion ha skärningspunkt med x -axeln?

c) är funktionen f (x) = w konstant²?

Svara på

Här är grafen för linjen x = 4:

Kan tjäna dig: statistiska variabler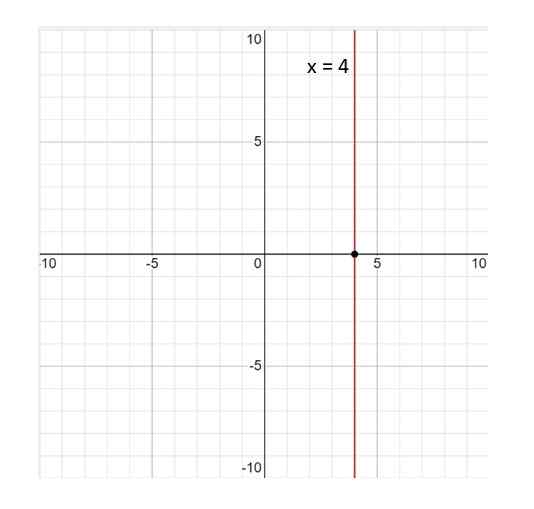 Figur 3. Graf över linjen x = 4. Källa: f. Zapata.

Linjen x = 4 är inte en funktion; Per definition är en funktion en relation som till varje värde på variabeln x Det motsvarar ett enda värde på och. Och i detta fall är detta inte uppfyllt, eftersom värdet x = 4 är associerad med oändliga värden på och. Därför är svaret nej.

Svar B

I allmänhet har en konstant funktion ingen skärningspunkt med axeln x, såvida det inte är y = 0, i vilket fall är det axeln x Ordentligt sagt.

Svar C

Ja, sedan W Det är konstant, dess fyrkant är också. Vilka intressen är det W Det beror inte på ingångsvariabeln x.

- Övning 2

Hitta korsningen mellan funktionerna f (x) = 5 och G (x) = 5x - 2

Lösning

För att hitta korsningen mellan dessa två funktioner kan de skrivas om respektive:

y = 5; y = 5x - 2

De matchas, erhåller:

5x - 2 = 5

Vilket är en första grads linjär ekvation, vars lösning är:

5x = 5+2 = 7

x = 7/5

Korsningspunkten är (7/5; 5).

- Övning 3

Visa att den som härrör från en konstant funktion är 0.

Lösning

Från definitionen av derivat du har:

 f (x) = k

f (x+h) = k

Ersätta definitionen:

Ovanstående är vettigt, eftersom derivatet av en funktion definieras som lutningen för linjen tangent till kurvan vid en given punkt. Den ständiga funktionen har en noll som väntar och alla tangentlinjer till den också.

Dessutom, om vi tänker på derivatet som en växelkurs Dy/dx, Den ständiga funktionen upplever inte någon förändring, därför är dess derivat ogiltigt.

Kan tjäna dig: multiplikativ princip: räkningstekniker och exempel

- Övning 4

Hitta den obestämda integrationen av f (x) = k.

Lösning

- Övning 5

Ett mobiltelefonföretag erbjuder obegränsad internettjänst med fast ränta som betalar $ 15 per månad. Vad är prisfunktionen enligt tiden?

Lösning

Låt P vara det pris som ska betalas vid $ och T -tiden, vilket kan uttryckas på dagar. Funktionen är etablerad enligt följande:

P (t) = 15

- Övning 6

Följande kontra Time -graf motsvarar rörelsen av en partikel.

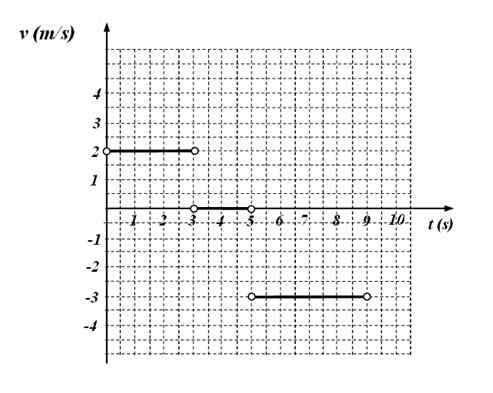Figur 4. Funktion V (t) Funktionsgraf för övning 6. Källa: f. Zapata.

Det begärs:

a) Skriv ett uttryck för hastighetsfunktion som en funktion av tiden V (t).

b) Hitta det avstånd som mobilen har kört i tidsintervallet mellan 0 och 9 sekunder.

Lösning till

Av grafen som visar att:

-V = 2 m/s I tidsintervallet mellan 0 och 3 sekunder

-Mobilen arresteras mellan 3 och 5 sekunder, eftersom hastigheten i detta intervall är värt 0.

-V = - 3 m/s Mellan 5 och 9 sekunder.

Det är ett exempel på en bit bit eller funktion i delar, som i sin tur består av konstant funktioner, endast giltigt för de angivna tidsintervallen. Det dras slutsatsen att den eftertraktade funktionen är:

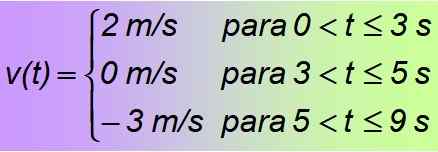
Lösning B

Från graf V (t) kan det avståndet som röret har beräknats, vilket numeriskt är lika med området lågt/på kurvan. Den här vägen:

-Avstånd som reste mellan 0 och 3 sekunder = 2 m/s . 3 s = 6 m

-Mellan 3 och 5 sekunder arresterades han, därför reste han inte något avstånd.

-Avstånd som reste mellan 5 och 9 sekunder = 3 m/s . 4 s = 12 m

Totalt turnerade mobilen 18 m. Se att även om hastigheten är negativ i intervallet mellan 5 och 9 sekunder, är det rest avståndet positivt. Vad som händer är att under det tidsintervallet hade mobilen ändrat betydelsen av dess hastighet.

Referenser

1. Geogebra. Konstantfunktioner. Återhämtat sig från: Geogebra.org.
2. Maplesoft. Konstantfunktionen. Återhämtat sig från: Maplesoft.com.
3. Wikilibros. Beräkning i en variabel/funktion/konstant funktion. Återhämtad från: är.Wikibooks.org.
4. Wikipedia. Konstant funktion. Hämtad från: i.Wikipedia.org
5. Wikipedia. Konstant funktion. Återhämtad från: är.Wikipedia.org.