Minskande funktion Hur man identifierar det, exempel, övningar

En minskande funktion f är en vars värde minskar när värdet på x ökar. Betyder att i ett givet intervall, med tanke på två värden x₁ och x₂ så att x₁ < x₂, sedan f (x₁)> f (x₂).

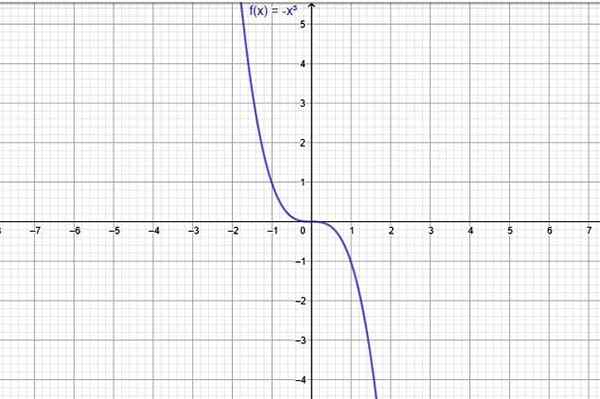
Ett exempel på en funktion som alltid minskar är f (x) = -x³, vars graf visar i följande figur:

Figur 1. En funktion som alltid minskar i hela domänen är f (x) = -x^3. Källa: f. Zapata genom geogebra.

Även om vissa funktioner som detta kännetecknas av att minska i alla deras domän, inte alla uppför sig så här, ökar det och även de som växer och minskar i vissa domänintervall. Studien av tillväxt och minskning av intervaller kallas monotoni av funktionen.

På samma sätt kan tillväxten eller minskningen av funktionen övervägas vid en viss domänpunkt. Men alla funktioner som minskar i ett givet intervall är också vid varje punkt som tillhör den.

[TOC]

Hur man identifierar en minskande funktion?

Funktionsgrafen indikerar visuellt om det minskar eller inte. Om det, när det rör sig i den ökande meningen av X, "sjunker" -funktionen, betyder det att den minskar.

Och om du har intervaller där det minskar och växer växelvis, vilket är det vanligaste, eftersom dessa tydligt avslöjas genom att observera beteendet hos funktionen i hela dess domän, eftersom det kommer att finnas intervaller där funktionen "stiger upp" och andra i vilken "stiger".

Alternativt, om funktionsgrafen inte är tillgänglig, är det analytiskt möjligt att avgöra om den minskar vid en punkt eller i ett intervall, genom det första derivatet.

Det första derivatet

Notera beteendet hos den minskande funktionen som visas i figur 2. De rosa linjesegmenten är tangent till de punkter vars koordinater är [en FA)] och [A+H, F (A+H)] och ha en negativ lutning.

Kan tjäna dig: Hur erhålls informationen i en undersökning?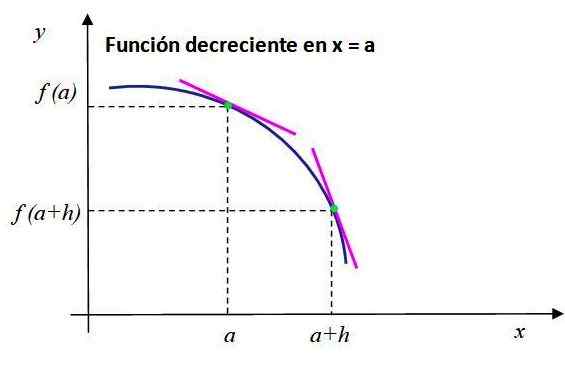figur 2. Lutningen på tangentlinjen till grafen för f (x) är negativ vid x = a, då minskar funktionen vid denna punkt. Källa: f. Zapata.

För den här funktionen uppfylls följande:

F (a+h) - f (a) < 0 ⇒  F (a+h) < f (a)

Därför kan man tänka att funktionen minskar i x = a.

Den första härledda från funktionen f (x), utvärderad vid x = a, som per definition är lutningen för tangentlinjen till kurvan vid x = a, ges av:

Gränsen indikerar att värdet på H kan göras så litet som du vill och föreslår att tecknet på fa), Det kan användas för att veta om funktionen minskar vid en viss punkt, så länge derivatet finns vid den punkten.

I så fall, ja fa) < 0, Det kan bekräftas att funktionen minskar och tvärtom, om f '(a)> 0, Då växer funktionen vid den punkten.

Teorem för minskande och växande funktioner

Tidigare hänvisades till funktionens beteende vid en punkt. Nu tillåter följande teorem att veta intervallen där en funktion minskar, växer eller konstant:

Låt f vara en differentierbar funktion i intervallet (a, b). Är det sant att:

-Ja f '(x) < 0 para todo x perteneciente a (a,b), entonces f(x) es decreciente en (a,b).

-Om tvärtom f '(x)> 0 för alla x som tillhör (a, b), sägs det att funktionen f (x) växer i (a, b).

-Slutligen, om f '(x) = 0 för alla x som tillhör intervallet (a, b), är f (x) konstant i nämnda intervall.

Demonstration

Anta att f '(x) < 0 para cualquier valor de x en el intervalo (a,b), además se tienen x₁ och x₂ tillhör nämnda intervall och villkoret att x₁< x₂.

Medelvärdet för satsen säger att det finns ett verkligt nummer C, mellan x₁ och x₂, Så att:

Kan tjäna dig: Vanlig faktor för grupperingsvillkor: Exempel, övningar

Som etablerat sedan x₁< x₂,  Δx är positiv. Så eftersom f '(c) är negativ, så är Δy också. Därför f (x₁) är större än f (x₂) Och funktionen minskar effektivt vid alla tider i intervallet (a, b).

Steg för att veta om en funktion minskar

För att hitta intervallen för minskning och tillväxt av en funktion genom att tillämpa föregående teorem följs dessa steg:

-Hitta den första härledda från funktionen och matcha den till noll, lösa den resulterande ekvationen. Bestäm också de punkter som derivatet inte finns.

Alla dessa punkter kallas kritiska punkter Och det är nödvändigt att hitta dem, eftersom i dem har derivatet möjlighet att ändra sitt tecken, vilket tyder på att funktionen går från att växa till minskning eller tvärtom.

-Funktionens domän delas upp i intervaller bestämda av de punkter som det första derivatet avbryts eller inte finns.

-Slutligen studeras tecknet på derivatet vid en godtycklig punkt som tillhör var och en av de intervall som erhållits i föregående steg.

Exempel på minskande funktioner

Funktionerna minskar inte alla i samma takt, vissa gör det snabbare än andra. Följande funktioner, som förekommer ofta i praktiken, minskar:

Den exponentiella funktionen

En funktion av form F (x) = a^x, Med en mellan 0 och 1, inte inklusive dessa, minskar snabbt under hela deras domän.

Funktion 1/x

Genom ett online -grafikprogram som en geogebra byggs grafen för funktionen f (x) = 1/x, vilket bekräftar att det minskar i hela domänen.

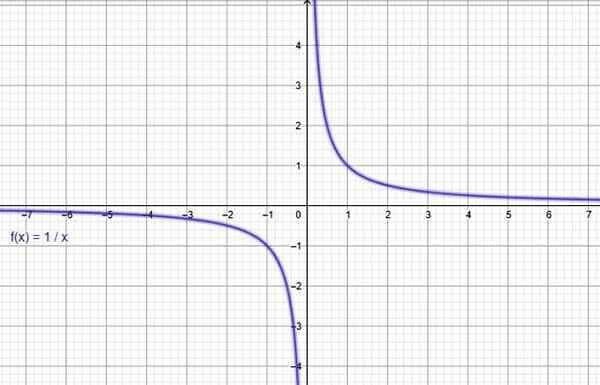Figur 3. Funktionen f (x) = 1/x minskar. Källa: f. Zapata genom geogebra.

Den relaterade funktionen

Funktionerna för formen y = mx + b med m<0 tienen gráficas que son rectas de pendiente negativa y por lo tanto son funciones decrecientes.

Kan tjäna dig: matematisk jämlikhet

Träning löst

Hitta, om någon, minskningsintervallen för funktionen:

f (x) = x⁴ - 6x² - 4

Lösning

Det första steget är att hitta f '(x):

f '(x) = 4x³ - 12x

Det första derivatet av f (x) är en kontinuerlig funktion, det vill säga det har inga diskontinuitetspunkter, men avbryts i:

4x³ - 12x = 0 = 4x (x²-3) = 0

Lösningarna på denna ekvation är: x₁ = 0, x₂ = - √3 och x₃ = √3. Dessa är de kritiska punkterna, som delar domänen för f (x) i intervallerna: (-∞,- √3); (- √3.0); (0, √3); (√3, ∞+).

Sedan utvärderas den första härledda i ett godtyckligt X -värde, som tillhör varje intervall. Dessa värden valdes:

För (-∞,- √3)

F '(-2) = 4 (-2)³ - 12x (-2) = -32+24 = -8

För (- √3.0)

F '(-1) = 4 (-1)³ - 12x (-1) = -4+12 = 8

För (0, √3)

f '(1) = 4 (1)³ - 12x (1) = 4-12 = -8

För (√3, ∞+)

f '(2) = 4 (2)³ - 12x (2) = 32-24 = 8

Liksom flera intervall är det en bra idé att skapa en tabell för att organisera resultaten. Den uppåtgående pilen indikerar att funktionen växer och ner, vilket minskar:

Det dras slutsatsen att funktionen minskar med intervaller (-∞,- √3) och (0, √3) och växer i de återstående intervallen. Den ursprungliga funktionen i Geogebra kontrolleras enkelt genom grafering.

Referenser

1. Ayres, f. 2000. Beräkning. 5ed. MC Graw Hill.
2. Leithold, L. 1992. Beräkning med analytisk geometri. Harla, s.TILL.
3. Purcell, E. J., Varberg, D., & Rigdon, s. OCH. (2007). Beräkning. Mexiko: Pearson Education.
4. Matemobil. Funktioner, växande, minskande och konstant. Återhämtad från: Matemovil.com
5. Stewart, J. 2006. Preccculment: Matematik för beräkning. Femte. Utgåva. Cengage Learning.