Injektionsfunktion vad den består av, vad är det för och exempel

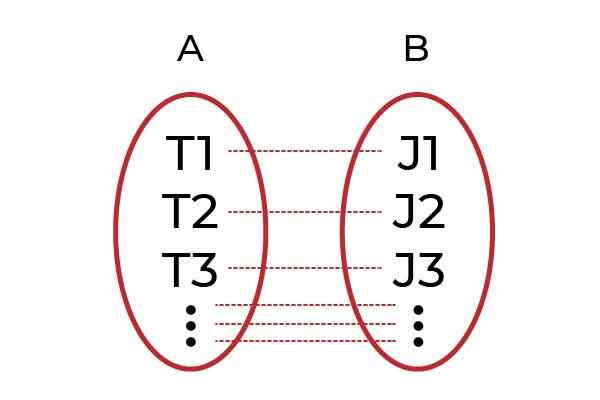
En Injektionsfunktion Det är alla förhållanden mellan domänelement med ett enda element av kodominium. Även känd som funktion en och en ( elva ), är en del av klassificeringen av funktioner angående hur deras element är relaterade.

Ett element av kodominium kan bara vara en bild av ett enda element i domänen, på detta sätt kan inte värden på den beroende variabeln upprepas.

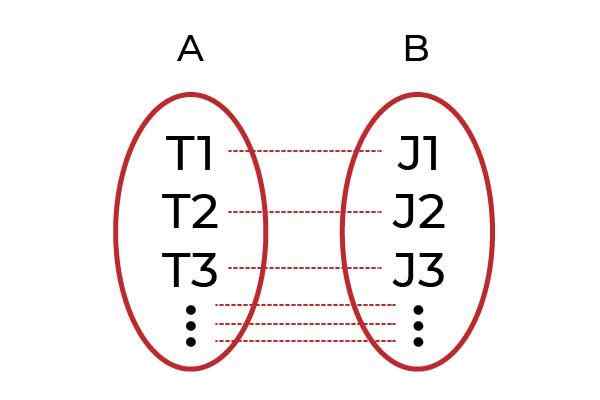
Källa: Författare.

Ett tydligt exempel skulle vara att gruppera män med arbete i en grupp A och i en grupp B till alla chefer. Funktionen F Det kommer att vara den som associerar varje arbetare med sin chef. Om varje arbetare är förknippad med en annan chef genom F, så F  Det kommer att vara en Injektionsfunktion.

Att överväga Injicering Följande måste uppfyllas till en funktion:

∀ x₁  ≠ x₂   ⇒ F (x₁ ) ≠ f (x₂ )

Detta är det algebraiska sättet att säga För alla x₁ skiljer sig från x₂ Du har en f (x₁ ) Skiljer sig från f (x₂ ).

[TOC]

Vad är injicerande funktioner för?

Injektivitet är en egenskap hos kontinuerliga funktioner, eftersom de säkerställer tilldelning av bilder för varje domänelement, väsentlig aspekt i kontinuiteten i en funktion.

När du ritar en linje parallell med axeln X På diagrammet för en injektionsfunktion bör endast grafen beröras vid en enda punkt, oavsett vilken höjd eller storlek på OCH Linjen ritas. Detta är det grafiska sättet att bevisa en funktions injektivitet.

Ett annat sätt att testa om en funktion är Injicering, rensar den oberoende variabeln X När det gäller den beroende variabeln OCH. Då bör det verifieras om domänen för detta nya uttryck innehåller de verkliga siffrorna, samtidigt som för varje värde på OCH det finns ett enda värde på X.

Beställningsfunktioner eller förhållanden följer bland andra former, notationen F: D_F→C_F

Som läser F det går från D_F till C_F

Där funktionen F RELATE SETS Domän och Kodominium. Även känd som startuppsättningen och ankomstuppsättningen.

Kan tjäna dig: slumpmässig provtagning: metodik, fördelar, nackdelar, exempel

Dominansen D_F  Innehåller de tillåtna värdena för den oberoende variabeln. Kodominiet C_F  Det bildas av alla tillgängliga värden för den beroende variabeln. Elementen i C_F relaterat till D_F  De vet hur Funktionsområde (R_F ).

Funktionskonditionering

Ibland kan en funktion som inte är injicerande genomgå viss konditionering. Dessa nya förhållanden kan förvandla det till en Injektionsfunktion. Alla typer av modifieringar av funktionen och kodominet för funktionen är giltiga, där målet är att uppfylla injektivitetsegenskaperna i motsvarande förhållande.

Exempel på injektiva funktioner med lösta övningar

Exempel 1

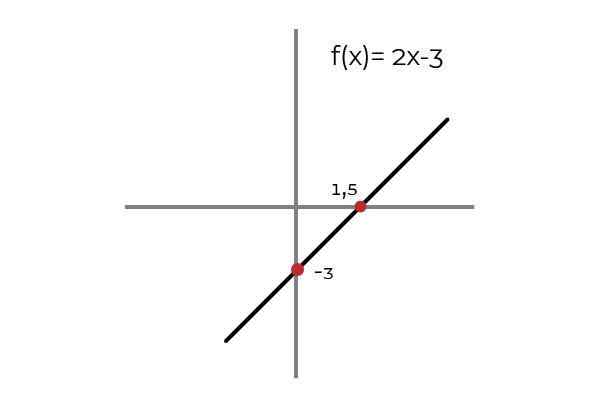
Vara funktionen F: r → R definieras av linjen F (x) = 2x - 3

A: [alla riktiga siffror]

Källa: Författare.

Det observeras att för alla domänvärden finns en bild i kodominiet. Den här bilden är unik, vilket gör en injektionsfunktion. Detta gäller alla linjära funktioner (funktioner vars större grad av variabeln är en).

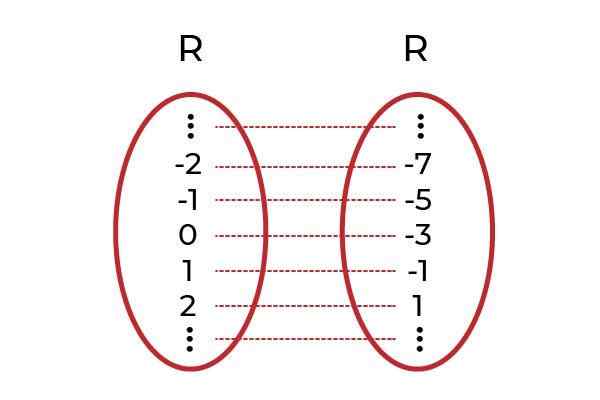Källa: Författare.

Exempel 2

Vara funktionen F: r → R definieras av F (x) = x² +1

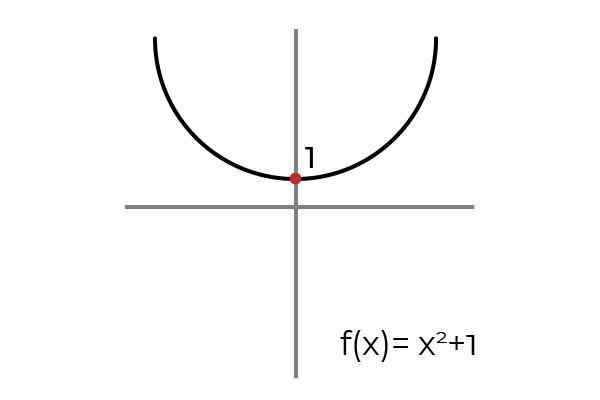Källa: Författare

När du ritar en horisontell linje observeras att grafen finns vid mer än ett tillfälle. På grund av detta F är inte injektion när du definieras  R → R

Funktionens domän är konditionerad:

                                               F: r⁺ ELLER 0 → R

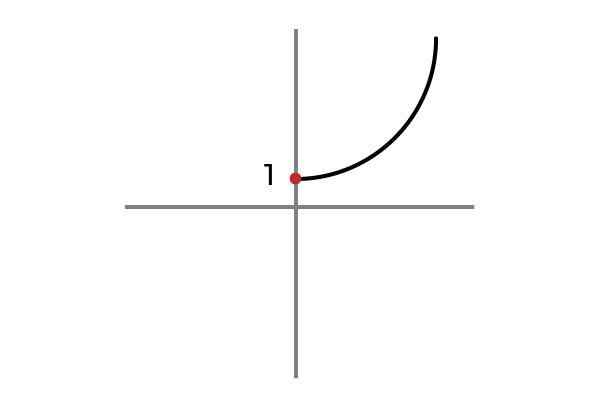Källa: Författare

Nu tar den oberoende variabeln inte negativa värden, på detta sätt undviks det att upprepa resultat och funktionen F: r⁺ ELLER 0 → R definieras av F (x) = x² + 1 är injektion.

En annan homolog lösning skulle vara att begränsa domänen till vänster, det vill säga begränsa funktionen för att endast ta negativa och nollvärden.

Funktionens domän är konditionerad

                                               F: r^- ELLER 0 → R

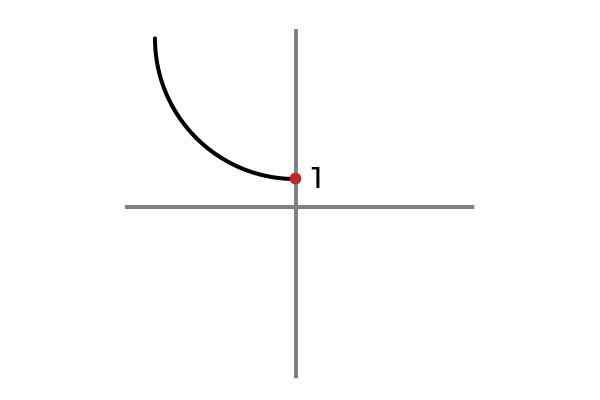Källa: Författare

Nu tar den oberoende variabeln inte negativa värden, på detta sätt undviks det att upprepa resultat och funktionen F: r^- ELLER 0 → R definieras av F (x) = x² + 1 är injektion.

Trigonometriska funktioner har beteenden som liknar vågor, där det är mycket vanligt att hitta repetitioner av värden i den beroende variabeln. Genom specifik konditionering, baserat på förkunskaper om dessa funktioner, kan vi begränsa domänen för att uppfylla injektivitetsförhållandena.

Kan tjäna dig: Coplanares Points: Ekvation, exempel och lösta övningar

Exempel 3

Vara funktionen F: [ -π/2, π/2 ] → R definieras av F (x) = cos (x)

I intervallet [ -π/2 → π/2 ] Kosinusfunktionen varierar sina resultat mellan noll och en.

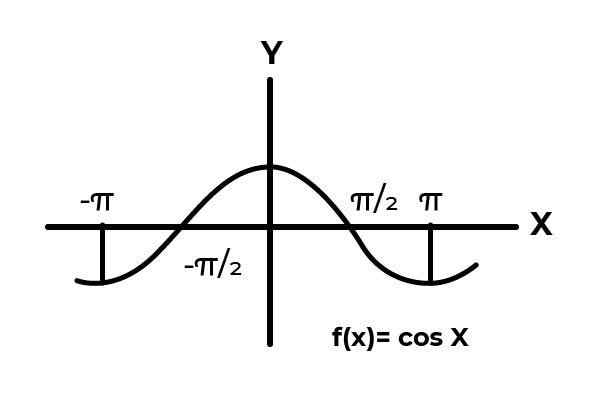Källa: Författare.

Som framgår av grafiken. Börja från början x = -π/2 når sedan maximalt noll. Det är efter x = 0 att värdena börjar upprepa, tills de återgår till noll i x = π/2. På detta sätt är det känt det F (x) = cos (x) är inte injektion För intervallet [ -π/2, π/2 ] .

När du studerar funktionsgrafiken F (x) = cos (x) Intervaller observeras där kurvanens beteende anpassar sig till injektivitetskriterierna. Som intervallet

[0 , π ]

Där funktionen varierar resultaten från 1 till -1, utan att upprepa något värde i den beroende variabeln.

På detta sätt funktionsfunktionen F: [0 , π ] → R definieras av F (x) = cos (x). Det är injektion

Det finns icke -linjära funktioner där liknande fall presenteras. För rationella uttryck, där nämnaren innehåller minst en variabel, finns det begränsningar som förhindrar relationens injektivitet.

Exempel 4

Vara funktionen F: r → R definieras av F (x) = 10/x

Funktionen definieras för alla riktiga siffror utom 0 som presenterar en obestämdhet (det kan inte delas mellan noll).

När du närmar sig noll till vänster tar den beroende variabeln mycket stora negativa värden, och omedelbart efter noll tar värdena på den beroende variabeln stora positiva figurer.

Denna störning gör uttrycket F: r → R definieras av F (x) = 10/x

Var inte injektion.

Som framgår av de tidigare exemplen tjänar uteslutningen av värden i domänen till att "reparera" dessa obestämningar. Noll är utesluten från domänen, lämnar uppsättningen och ankomstuppsättningarna definierade på följande sätt:

R - 0 → R

Var R - 0 symboliserar det verkliga förutom en uppsättning vars enda element är noll.

På detta sätt uttrycket F: R - 0 → R definieras av F (x) = 10/x är injektion.

 Exempel 5

Vara funktionen F: [0 , π ] → R definieras av F (x) = sin (x)

I intervallet [0 , π ] Sinusfunktionen varierar sina resultat mellan noll och en.

Kan tjäna dig: slumpmässig variabel: koncept, typer, exempel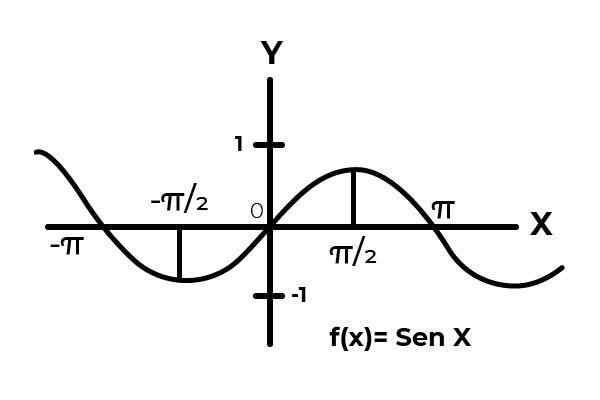Källa: Författare.

Som framgår av grafiken. Börja från början x = 0 sedan når ett maximum i x = π/2. Det är efter x = π/2 som värdena börjar upprepas, tills de återgår till noll i x = π. På detta sätt är det känt det F (x) = sin (x) är inte injektion För intervallet [0 , π ] .

När du studerar funktionsgrafiken F (x) = sin (x) Intervaller observeras där kurvanens beteende anpassar sig till injektivitetskriterierna. Som intervallet  [  π/2,3π/2  ]

Där funktionen varierar resultaten från 1 till -1, utan att upprepa något värde i den beroende variabeln.

På detta sätt funktionen F: [  π/2,3π/2  ] → R definieras av F (x) = sin (x). Det är injektion

Exempel 6

Verifiera om funktionen F: [0, ∞) → R definieras av F (x) = 3x² Det är injektion.

Vid detta tillfälle är uttryckets domän redan begränsad. Det observeras också att de beroende variabla värden inte upprepas i detta intervall.

Därför kan man dra slutsatsen F: [0, ∞) → R definieras av F (x) = 3x²   Det är injektion

Exempel 7

Identifiera vilka av följande funktioner är

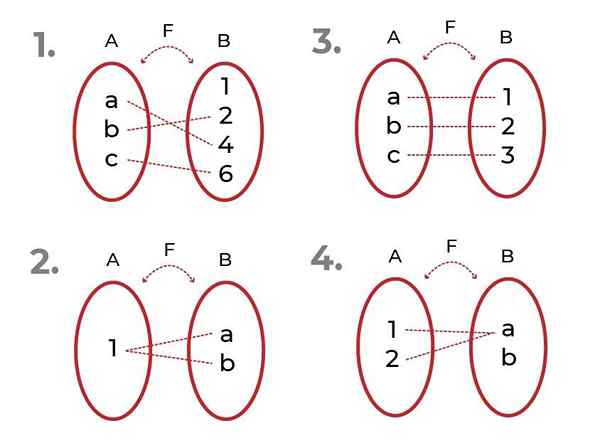Källa: Författare

1. Det är injektion. De tillhörande elementen i kodominiet är unika för varje värde på den oberoende variabeln.
2. Det är inte injektion. Det finns element i Co -Coominium associerade med mer än ett element i startuppsättningen.
3. Det är injektion
4. Det är inte injektion

Föreslagna övningar för klass/hus

Kontrollera om följande funktioner är injektiva:

F: [0, ∞) → R definieras av F (x) = (x + 3)²  

F: [ π/2,3π/2  ] → R definieras av F (x) = tan (x)

F: [ -π,π  ] → R definieras av F (x) = cos (x + 1)

F: r → R definieras av linjen F (x) = 7x + 2

Referenser

1. Introduktion till logik och kritiskt tänkande. Merrilee h. Lax. University of Pittsburgh
2. Problem i matematisk analys. Piotr Bilar, Alfred Witkowski. University of Wroclaw. Pol.
3. Delar av abstrakt analys. Mícheál O'Searcoid PhD. Institutionen för matematik. University College Dublin, Beldfield, Dublind 4.
4. Introduktion till logik och metodik för de deduktiva vetenskaperna. Alfred Tarski, New York Oxford. Oxford University Press.
5. Matematiska analysprinciper. Enrique Linés Escardó. Redaktionella återkomster. Till 1991. Barcelona, ​​Spanien.