Euklidisk geometri

Vi förklarar vad euklidisk geometri, dess historia, element och vi ger flera exempel är

Euclid från Alexandria och dess element, av Jusepe de Ribera, bredvid, två icke -parallella linjer och en linje som skär dem, illustrerar det femte postulatet. Källa: Wikimedia Commons.

Vad är euklidisk geometri?

De Euklidisk geometri Det är den som styrs av de postulaten av Euclid de Alejandría, en grekisk geometer som levde mot 300 till.C, i vars ära denna disciplin heter, eftersom den var den första som systematiserar den.

Denna gren av matematik studerar egenskaperna för linjer, plan, vinklar och geometriska figurer som polygoner, omkretsar och andra koniker. Därmed dess betydelse inom vetenskap och teknik, vars utveckling ledde till betydligt.

Å andra sidan var euklidisk geometri den första exakta vetenskapen, eftersom med den väg för systematisering av vetenskapen började, liksom användningen av logik för att demonstrera, från några axiomer, många förslag som kallas teorem för att beskriva egenskaperna av geometriska föremål.

Historia

Geometri har en lång historia, eftersom mänsklighetens intresse i den är mycket gammal och den centrala axeln för euklidisk geometri är arbetet Föremål, av den kloka eukliden i Alexandria, en stad belägen i Egypten och som bodde under det fjärde århundradet för att.C.

Vid den tidpunkten var de viktigaste egenskaperna hos många figurer och geometriska organ kända. Det fanns omfattande kunskap om geometri, men allt var empiriskt och saknade systematisering.

Sedan anförde kungen av Egypten Ptolemy och anförde den redan berömda Euclid -läraren, vars skola var i Alexandria, för att organisera all matematisk och geometrisk kunskap hittills, inklusive teorier och egenskaper.

Euclides fick arbeta och bredvid sina lärjungar skrev sina arbetselement, som han delade upp i tretton böcker, som kapitel. Detta arbete skulle bli en referens för geometri för kommande generationer.

Kan tjäna dig: successiva derivat

Element av euklid

Innehållet i elementen är organiserat enligt följande:

• I böcker utvecklas jag till IV platt geometri.
• I böcker V och jag såg proportionens teori.
• Ix -böcker är dedikerade till aritmetik.
• Oförsåglighet visas i bok x,
• Space Geometry i böcker xi till xiii.

Euklidisk geometri var grunden för många bakre geometriska utvecklingar och undervisas för närvarande i alla skolor i världen.

Det har också fördelen att vara det första arbetet som inkluderar noggranna demonstrationer baserade på logisk resonemang, och även för att ge sammanhållning till kroppen av geometrisk och matematisk kunskap från den tiden.

Grundläggande element i euklidisk geometri

Euklidisk geometri är byggd runt fyra grundelement, beskrivna i bok I av elementen:

1. Fläck
2. Hetero
3. Platt
4. Plats

1. Fläck

En fläck Det saknar dimensioner eller delar och skiljer sig från en annan punkt helt enkelt efter dess plats. Om två punkter A och B är olika beror det på att de har olika positioner, som indikeras genom de välkända kartesiska koordinaterna (x, y) om punkten är i planet, eller koordinaterna (x, y, z) om det är i rymden.

Det är anmärkningsvärt att det kartesiska systemet inte är en del av Föremål av Euclid, men dök upp mycket senare på 1600 år och beror på René Descartes.

2. Hetero

De hetero Det är en oändlig samling av poäng, och den har bara längd, inte bredd. En del av den dras vanligtvis, med pilar i båda påpekar att linjen fortsätter på obestämd tid.

3. Platt

En platt Det är en obegränsad yta, så den har två dimensioner och som en del representeras med hjälp av en kvadrat eller en rektangel.

Där, i planet, finns det många geometriska figurer, såsom linjer, öppna och stängda kurvor och polygoner, bland andra.

Kan tjäna dig: Allmän ekvation av en linje vars lutning är lika med 2/3

4. Plats

Slutligen finns det Plats Med sina tre dimensioner, kapabla att höja alla punkter. Den innehåller planen och geometriska kroppar som kännetecknas av deras volym, till exempel polyhedra, sfärer och mer.

Dessa kan betraktas som de grundläggande definitionerna av euklidisk geometri, men utöver dessa erbjuder Euclides cirka 150 varierande definitioner i sitt arbete.

Vanliga uppfattningar

De består av uppenbara och intuitiva fakta, som inte tillhör ordentligt till geometriens omfattning och används som koncept utvecklas. De hänvisar till "saker" i ett mycket brett sammanhang:

1. Saker samma sak som något annat, de är samma med varandra.
2. Om saker läggs till i en annan uppsättning saker, och alla är desamma, vilka resultat är också desamma.
3. Om lika saker är stulna är de återstående också densamma.
4. När saker sammanfaller med varandra beror det på att de är desamma.
5. Hela är alltid större än parterna, tas separat.

Postulat av euklidisk geometri

Postulat eller axiomer är enkla uttalanden som anses vara sanna och uppenbara, så de kräver inte demonstration.

De utgör grunden för Euclidian och euklidgeometri etablerar fem i sin bok I:

1. Vara två olika punkter till och b, det finns bara en rad som passerar genom dem, det vill säga två punkter bestämmer en linje.
2. Alla rätlinjiga segment kan förlängas på obestämd tid för att utgöra en linje, därför tillhör varje segment en linje.
3. Om du har två olika punkter eller och en kan du alltid rita en cirkel med mitt i O och radie lika med OA -segmentet.
4. Alla raka vinklar överensstämmer med varandra.
5. Med tanke på en linje och en punkt P som inte tillhör den är det alltid möjligt.

Det sista postulatet, särskilt i sin ursprungliga version, ser inte så enkelt ut som de andra. Det säger att:

Kan tjäna dig: Hepagon

"Om en rak linje som faller på två andra linjer, gör de två inre vinklarna på samma sida mindre än två raka vinklar, säger raka linjer, utbredd på obestämd tid, är de (korsar) på sidan som de mindre vinklarna är att de två raka vinklar ".

Det vill säga, ursprungligen postulat 5 fastställer tillståndet så att två rader inte är parallella. Men det är tydligare när det är skrivet på ett sådant sätt att det illustrerar det motsatta, det vill säga linjens parallellism.

Exempel på euklidisk geometri

Exempel 1

Det finns tre olika punkter, märkta med bokstäver A, B och C.

1. Hur många olika linjer går igenom punkt a?
2. Och hur många som kan dras mellan punkterna A och B? Och mellan A och C?
3. Är det möjligt att rita en linje till vilken punkterna A, B och C?

Svara på

Enligt postulat I kan oändliga raka linjer dras genom A, eftersom två punkter krävs för att bestämma en linje.

Svar B

Entre A och B kan bara dras en linje. Och mellan A och C också.

Svar C

Det är inte möjligt för en linje att innehålla A, B och C samtidigt.

Exempel 2

Det uppmanas att bygga steg för steg en liksidig triangel (alla dess sidor är lika), och känner till en av dess sidor, som är AB -segmentet och indikerar i varje steg postulatet eller den vanliga uppfattningen som används i konstruktionen i.

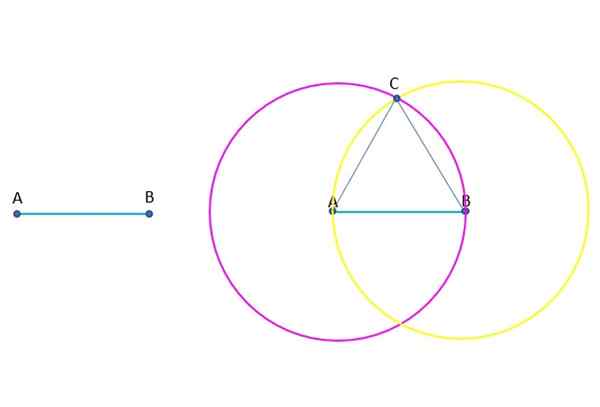Konstruktion av ABC -liksidig triangel. Källa: f. Zapata.

Svar

Steg 1

En cirkel med ett centrum i A och Radio AB ritas. Detta är alltid möjligt, enligt Postulate III.

Steg 2

En annan omkrets med centrum i B och radio AB dras och postulatet III appliceras igen.

Steg 3

Båda omkretsarna, som har samma radie, skärs vid punkt C. Nu kan du rita segment som förenar C med A respektive B, enligt postulat i.

Dessa segment är radioapparater och därför är måtten på AC och BC lika med AB, enligt den vanliga uppfattningen 1. Då är ABC -triangeln liksidig.