Pythagorean identitetsdemonstration, exempel, övningar

Are Pythagorean identitet Alla trigonometriska ekvationer som uppfylls för alla vinkelvärden och är baserade på Pythagoras teorem. Det mest kända av Pythagorean -identiteter är den grundläggande trigonometriska identiteten:

Sen²(α) + cos²(α) = 1

Figur 1. Pythagorean trigonometriska identiteter.

Det är fortfarande i betydelse och använder den pythagoreiska identiteten hos tangenten och Secant:

Så²(α) + 1 = sek²(α)

Och den Pythagorean trigonometriska identiteten som involverar cotangenten och skördaren:

1 + CTG²(α) = CSC²(α)

[TOC]

Demonstration

De trigonometriska skälen bröst och cosinus De representeras i en radieomkrets en (1) känd som trigonometrisk cirkel. Denna cirkel har ett centrum vid koordinaternas ursprung eller.

Vinklarna mäts från den positiva halvaxeln för X, till exempel vinkeln a i figur 2 (se senare). I motsats till klockhänderna om vinkeln är positiv och i riktning mot händerna om det är en negativ vinkel.

Semi -rätten med ursprung eller och vinkel a ritas, vilket avlyssnar enhetscirkeln vid punkt P. Punkt P projiceras ortogonalt på den horisontella axeln X och ger upphov till punkt C. På liknande sätt projiceras P vinkelrätt på den vertikala axeln och ger upphov till punkt S.

Du har rätt OCP -triangel i C. 

Bröstet och kosinus

Det bör komma ihåg att trigonometrisk anledning bröst Det definieras på en höger triangel enligt följande:

Skötet i en vinkel i triangeln är förhållandet eller förhållandet mellan kateto som motsätter sig vinkeln och hypotenusen i triangeln.

Tillämpad på OCP -triangeln i figur 2 skulle vara så här:

Sin (α) = cp / op

Men CP = OS och OP = 1, så att:

SIN (α) = OS

Vilket innebär att projektionen på y -axeln har ett värde lika med den visade vinkeln. Det bör noteras att det maximala värdet på en vinkel bröst (+1) inträffar när a = 90º och det minsta (-1) när α = -90º eller α = 270º.

Kan tjäna dig: Vector Space: Base and Dimension, Axioms, Egenskaper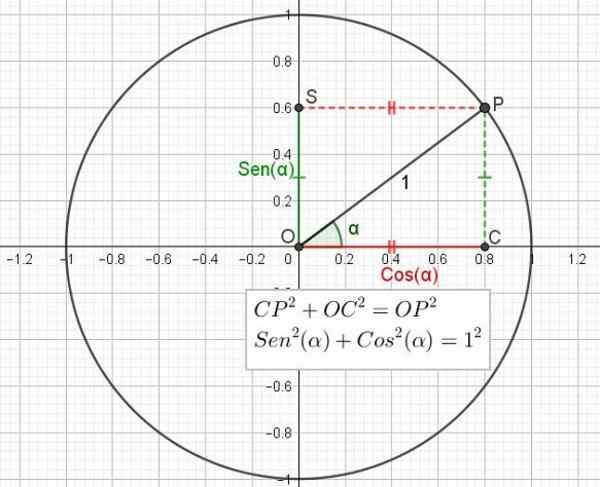figur 2. Trigonometrisk cirkel som visar förhållandet mellan Pythagoras teorem och grundläggande trigonometrisk identitet. (Egen utarbetande)

På liknande sätt är kosinus i en vinkel förhållandet mellan kategorin intill vinkeln och hypotenusen i triangeln.

Tillämpad på OCP -triangeln i figur 2 skulle vara så här:

Cos (α) = oc / op

Men op = 1, så att:

Cos (α) = oc

Vilket innebär att OC -projektionen på x -axeln har ett värde som är lika med det för den visade vinkeln. Det bör noteras att det maximala värdet för kosinus (+1) inträffar när a = 0º eller α = 360º, medan kosinans minimivärde är (-1) när a = 180º.

Den grundläggande identiteten

För rektangeln OCP -triangel tillämpas Pythagoras teorem, vilket säger att summan av kvadratet för kategorierna är lika med hypotenusens kvadrat:

Cp² + Oc² = OP²

Men det har redan sagts att Cp = Os = sin (α), att OC = cos (α) och att OP = 1, så det föregående uttrycket kan skrivas om beroende på sinus och kosinus i vinkeln:

Sen²(α) + cos²(α) = 1

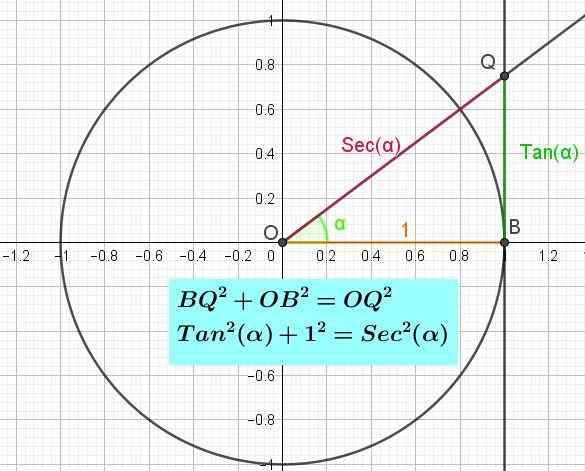
Tangentaxeln

Precis som X -axeln i den trigonometriska cirkeln är kosinusens axel och axeln och bröstets axel, på samma sätt finns tangentens axel (se figur 3) som är exakt linjen tangent till enheten cirkel vid punkten vid punkt B -koordinaten (1, 0). 

Om du vill veta värdet på tangenten i en vinkel dras vinkeln från den positiva semi -axeln för X, skärningspunkten mellan vinkeln med tangentens axel definierar en punkt Q, längden på OQ -segmentet är vinkelns tangent.

Kan tjäna dig: algebraiska derivat

Detta beror på att per definition är tangenten av vinkel a motsatt Cateto QB mellan den intilliggande Cateto OB. Det vill säga (α) = QB / OB = QB / 1 = QB.

Figur 3. Den trigonometriska cirkeln som visar tangentens axel och den tangentens pytagoreiska identitet. (Egen utarbetande)

Tangentens pytagoreiska identitet

Den pythagoriska identiteten hos tangenten kan demonstreras om rektangeln triangeln i B (figur 3) beaktas (figur 3). Tillämpa Pythagoras teorem på den triangeln du måste BQ² + Ob² = Oq². Men det har redan sagts att Bq = solbränna (α), att ob = 1 och att oq = sec (α), så att det ersätter pythagoras jämlikhet för rätt triangel obq den har:

Så²(α) + 1 = sek²(α).

Exempel

Kontrollera om Pythagorean identiteter är uppfyllda i rektangeln Triangeln i Catetos AB = 4 och BC = 3.

Lösning: Kategorierna är kända, det är nödvändigt att bestämma hypotenusen, vilket är:

AC = √ (AB^2 + BC^2) = √ (4^2 + 3^2) = √ (16 + 9) = √ (25) = 5.

Vinkeln ∡bac kommer att kallas α, ∡bac = α. Nu bestäms de trigonometriska skälen:

Sin α = BC / AC = 3/5 

COS a = AB / AC = 4/5 

Tan α = BC / AB = 3/4 

Cotan α = AB / BC = 4/3 

SEC α = AC / AB = 5/4 

CSC α = AC / BC = 5/3

Det börjar med grundläggande trigonometrisk identitet:

Sen²(α) + cos²(α) = 1

(3/5)^2 + (4/5)^2 = 9/25 + 16/25 = (9 +16)/25 = 25/25 = 1

Det dras slutsatsen att det är uppfyllt.

- Nästa Pythagorean identitet är tangentens:

Så²(α) + 1 = sek²(α)

(3/4)^2 + 1 = 9/16 + 16/16 = (9 + 16)/16 = 25/16 = (5/4)^2

Och det dras slutsatsen att tangentens identitet verifieras.

- På samma sätt det för cotangenten:

Kan tjäna dig: slumpmässiga val med eller utan ersättning

1 + CTG²(α) = CSC²(α)

1+ (4/3)^2 = 1 + 16/9 = 25/9 = (5/3)^2

Det dras slutsatsen att det också är uppfyllt, vilket har slutfört uppgiften att verifiera de pytagoreiska identiteterna för den givna triangeln.

Löst övningar

Testa följande identiteter, baserat på definitionerna av trigonometriska skäl och pytagoriska identiteter.

Övning 1

Bevisa vad cos² x = (1 + sen x) (1 - sin x).

Lösning: Den rätta medlemmen känner igen den anmärkningsvärda produkten från multiplikationen av ett binomial med dess konjugat som, som är känt, är en skillnad i rutor:

Cos² x = 1² - Sen² x

Sedan passerar termen med bröst på höger sida till vänster sida med det förändrade tecknet:

Cos² X + sen² x = 1

Noterar att den grundläggande trigonometriska identiteten har uppnåtts, så det dras slutsatsen att det givna uttrycket är en identitet, det vill säga det uppfylls för alla värde på x.

Övning 2

Från och med den grundläggande trigonometriska identiteten och använda definitionerna av trigonometriska skäl för att demonstrera skördarens pytagoreiska identitet.

Lösning: Den grundläggande identiteten är:

Sen²(x) + cos²(x) = 1

Båda medlemmarna är uppdelade mellan SEN²(x) och nämnaren distribueras i den första medlemmen:

Sen²(x)/synd²(x) + cos²(x)/synd²(x) = 1/sen²(x)

Det är förenklat:

1 + (cos (x)/sen (x))^2 = (1/sin (x))^2

Cos (x)/sin (x) = cotan (x) är en identitet (icke -Pythagorean) som verifieras av definitionen av trigonometriska skäl. På samma sätt inträffar det med följande identitet: 1/sin (x) = csc (x).

Äntligen måste du:

1 + CTG²(x) = csc²(x)

Referenser

1. Baldor J. (1973). Platt geometri och utrymme med en introduktion till trigonometri. Centralamerikansk kultur. C.TILL.
2. C. OCH. TILL. (2003). Geometrielement: med övningar och kompassgeometri. University of Medellin.
3. Campos, f., Cerecedo, f. J. (2014). Matematik 2. Patria Redaktionsgrupp.
4. Iriger. (s.F.). Matematik första termin Tacaná. Iriger.
5. Jr. Geometri. (2014). Polygoner. Lulu Press, Inc.
6. Miller, Heeren och Hornsby. (2006). Matematik: Resonemang och applikationer (tionde upplagan). Pearson Education.
7. Patiño, m. (2006). Matematik 5. Redaktionell progreso.
8. Wikipedia. Trigonometri -identiteter och formler. Återhämtad från: är.Wikipedia.com