Linjär interpolation

Vi förklarar vad som är den linjära interpoationen, dess formler, hur man gör en, med exempel och övningar löst

Vad är linjär interpolation?

De Linjär interpolation Den består av att uppskatta platsen för en punkt inom ett numeriskt intervall, förutsatt att de extrema värdena för nämnda intervall är förenade med en linje. Känd ekvationen för denna linje är det möjligt att hitta den okända punkten.

Idén är schematiserad i följande figur, som visar en metod för grafen över en funktion mellan punkterna A och B. Förutsatt att dessa punkter är nära är det möjligt att närma sig kurvan som förenar dem genom en linje och därmed hitta mellanpunkterna.

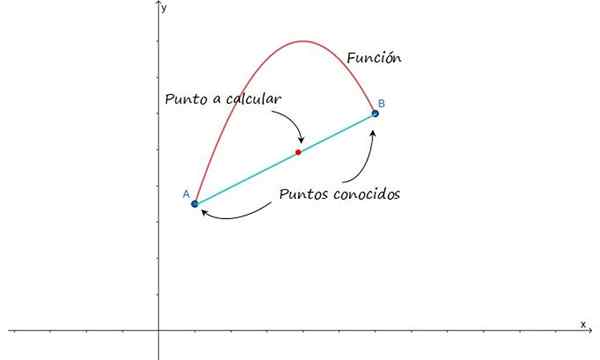Figur 1.- För att göra en linjär interpolering mellan punkterna A och B måste det antas att de är förenade med en linje . Källa: f. Zapata.

Du kan också ungefärliga kurvan som går med i punkterna med hjälp av en kvadratisk funktion eller annan polynom. Linjen har emellertid fördelen med sin matematiska enkelhet, så det är lätt att hantera, även om det är den enklaste interpolationen av alla, är det möjligt att resultatet inte är så exakt som det som erhålls genom att använda andra funktioner.

Formler

Det finns två koordinatpunkter [x_antingen, f (x_antingen)] och [x₁, f (x₁)] bland vilka är punkten [x, g (x)], vars koordinater vill veta.

Det första steget består i att gå med de kända punkterna genom ett linjesegment, på vilket koordinaterna för punkten en beräkning hittas.

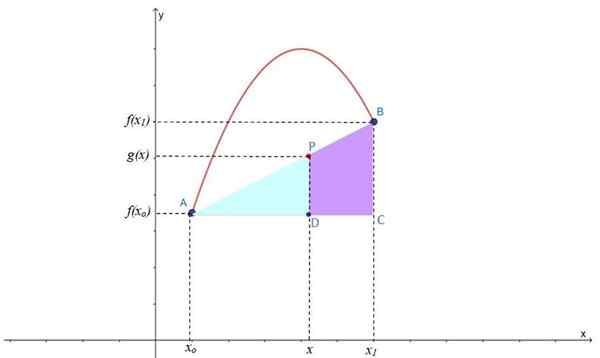figur 2.- Linjär interpolering för att hitta punkt P på interpoching -linjen g (x), belägen mellan punkterna a och b av f (x). Källa: f. Zapata.

Som ni ser bildas två rektanglar: ABC och APD, som också har en akut vinkel gemensamt, så de är liknande trianglar, till vilka Thales -teoremet kan appliceras:

Det kan tjäna dig: analytisk geometri

Genom att ersätta måtten på segmenten enligt grafen erhålls följande förhållande:

Därifrån fortsätter vi att rensa g (x):

 Kallelse:

F₁(x₁) = y₁ ; F_antingen(x_antingen) = y_antingen ; g (x) = y

Den översta ekvationen förvandlas till:

Felavstånd

När en funktion närmar sig med denna metod ges felnivån med det absoluta värdet på skillnaden mellan funktionen F (x) och interpolationslinjen g (x):

Fel = │f (x) - g (x) │

Hur man gör linjär interpolation?

Att utföra en linjär interpolering är väldigt enkelt, du måste bara följa dessa steg:

Steg 1

Bestäm den okända punkten P (x, y).

Steg 2

Upprätta de två punkterna som begränsar intervallet där värdet som ska beräknas är beläget, det vill säga punkterna (x x_antingen,och_antingen) och (x₁, och₁).

Steg 3

Byt ut alla värden i ekvationen:

Och beräkna resultatet.

Exempel på linjär interpolation

Exempel 1

Du vill hitta det ungefärliga värdet på Ln 3 genom linjär interpolering, med tanke på följande värden:

ln 2 = 0.693147 och ln 4 = 1.386294

Jämför resultatet med värdet på Ln 3 som erhållits genom en kalkylator och bestäm den åtagade marginalen.

• Steg 1

För att hitta det ungefärliga värdet på Ln 3 måste du fortsätta följande sätt: För det första är det okända, vilket är y = ln 3, bredvid dess motsvarande värde på "x": x = 3. Detta är poängen som du vill beräkna: (3, ln 3).

• Steg 2

Då måste du fastställa gränspunkterna för intervallet med de kända värdena. Det uppmanas att göra det med nästa par poäng:

• Lägre gräns: [x_antingen = 2; och_antingen = ln 2 = 0.693147]
• Övre gräns: [x₁ = 4; och₁ = ln 4 = 1.386294]

• Steg 3

Värdena som bestäms i steg 1 och 2 ersätts noggrant i ekvationen för att generera resultatet av tillvägagångssättet till LN 3:

Kan tjäna dig: hur många lösningar har en kvadratisk ekvation?

Det verkliga värdet på Ln 3 som erhålls av kalkylatorn är:

ln 3 = 1.098612

Och felmarginalen är:

Fel = │1.098612 - 1.03971 │ = 0.059

Interpolationens procentuella fel beräknas genom att dela felet mellan det verkliga värdet på LN3 och multiplicera med 100 %:

Procentandelfel = (verkligt fel/värde) × 100 = (0.059/1.098612) × 100% = 5.4%

Exempel 2

Nu vill du hitta det ungefärliga värdet på Ln 3 genom linjär interpolering, kända dessa två värden:

ln 2.5 = 0.916291 och ln 3.5 = 1.252763

Bestäm också motsvarande fel och jämför med resultaten från föregående exempel.

• Steg 1

Återigen är den okända punkten:

y = ln 3, x = 3

• Steg 2

• Lägre gräns: [x_antingen = 2.5; och_antingen = y_antingen = ln 2.5 = 0.916291]
• Övre gräns: [x₁ = 3.5; och₁ = ln 3.5 = 1.252763]

• Steg 3

Undersöker värdet som erbjuds av räknaren:

ln 3 = 1.098612

Felnivån bestäms i detta fall, vilket resulterar:

Fel = │1.098612 - 1.084527 │ = 0.014

Procentandelfelet i detta fall är ≈ 1.3 %. Jämfört med felnivån i exempel 1 är det nya värdet mer exakt, eftersom det intervall som valts till interpolär är lägre.

Löst övningar

Övning 1

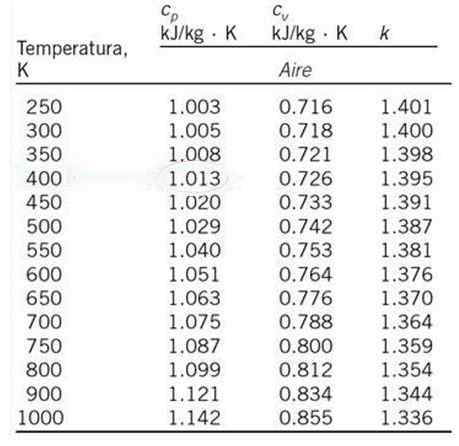
Beräkna, genom linjär interpolering, luftens specifika värme vid konstant tryck C_p  och temperaturen på 530 K, från och med värdentabellen som visas nedan.

• Lösning

I upplösningen av många problem är det vanligt att värdet som söks inte verkar exakt som önskvärt i värdentabellen. Ett alternativ är att välja det värde som är närmast den önskade, men många gånger är en linjär interpolation tillräckligt för att hitta ett mycket bättre tillvägagångssätt.

Kan tjäna dig: tecken på gruppering

Värdet på C_p En 530 K visas inte i den bifogade tabellen, men en linjär interpolering kan göras med respektive specifika värme vid 500 K och 550 K, som är temperaturen som är närmast 530 K och vars specifika värme visas i tabellen som visas.

De respektive specifika värmevärmerna för dessa temperaturer är:

T_antingen = 500 K; c_po = 1.029 kJ /kg ∙ k

T₁ = 550 K; c_P1 = 1.040 kJ /kg ∙ k

Och det okända är poängen (500k, c_p)

Ersätter i formeln för den linjära interpolationen ovan, med T på platsen för variabeln "X" och C_p Istället för "y" har du:

Övning 2

Den belastning som appliceras på en fjäder (i kilopondios) producerar följande töjningar (i millimeter) enligt tabellen som visas:

Beräkna förlängning när lasten är 12.6 kp.

• Lösning

Låt och värdet på den eftertraktade förlängningen när lasten är c ​​= 12.6 kp. Den okända punkten är (12.6, y), som är bland punkterna:

C_antingen = 10 kp; och_antingen = 105 mm

C₁ = 15 kp; och₁ = 172 mm

Det återstår bara att ersätta värdena i ekvationen:

Föreslagen träning

Beräkna den specifika värmevärmen till en konstant volym för en temperatur på 727 K med hjälp av linjär interpolering och tabellen över värdepapper i övningen löstes 1.

Referenser

1. Rafa Vilchez Academy. Hur man utför linjär interpolation. Återställt från: Academiraafavilchez.com
2. Chapra, s. 2007. Numeriska metoder för ingenjörer. Femte. Utgåva. McGraw Hill.
3. Khan akademin. Matematik för linjär interpolation. Återhämtat sig från: Khanacademy.org.
4. Utbildningslivet. Linjär interpoleringsformel. Återhämtad från: TheeducationLife.com
5. X-ingenjör. Linjär interpolering och extrapolering med kalkylator. Återhämtat sig från: X-Engineer.org.