Homologa sidor

Vi förklarar vad de homologa sidorna är, med exempel och övningar löst

Vad är homologa sidor?

De homologa sidor I två platta geometriska figurer är de som motsvarar varandra och håller likheten. Till exempel är en persons högra hand homolog med en annan persons högra hand.

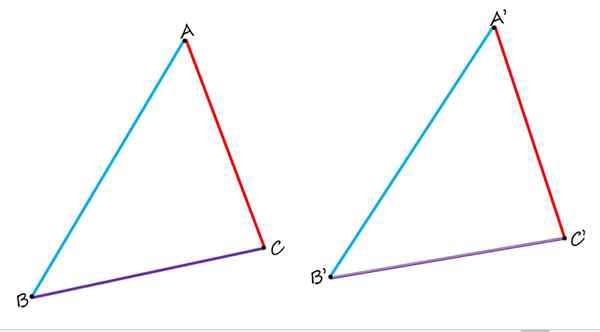
I platt geometri finns det inte bara homologa sidor, utan också vertikaler och homologa vinklar. För att se det, överväg följande figur, som består av två identiska trianglar ABC och A'B'C ':

I de två identiska trianglarna är AB och A'B 'homologa, liksom sidor BC och B'C' och AC och A'C '. Källa: f. Zapata.

Vid jämförelse av dem observeras det tydligt att sidorna ab och a'b 'i blått är homologa, eftersom de har en liknande position i varje triangel. Sidorna bc och b'c 'i lila är också homologa. Och slutligen är den röda AC -sidan homolog med sidan A'C '.

Förklaring

Från ovannämnda följer det att de homologa sidorna är de som upptar samma relativa position i figurer på samma sätt. I föregående bild användes två identiska trianglar för att visa idén, men detta kan enkelt generalisera andra platta geometriska figurer, bildade av på varandra följande sidor som stängs.

Dessa siffror kallas polygoner. Till exempel är trianglar och fyrkantiga polygoner på 3 respektive 4 sidor.

Begreppet homologa sidor är viktigt eftersom det gör det möjligt att definiera likhetskriterier mellan polygoner, vilket kommer att ses inom kort. De liknande siffrorna har exakt samma form och håller identisk proportion mellan sina sidor, även om de inte är samma storlek.

Och även om det hittills hänvisades till platta siffror, finns det också liknande siffror i tre dimensioner. De observeras lätt i stormarknadshyllor, när samma produkt säljs i identiska containrar, men med en annan storlek.

Kan tjäna dig: matematisk logik

Andra ord som används omväxlande i geometri för att hänvisa till homologa sidor i geometriska figurer är: motsvarande sidor, respektive sidor och motsvarande sidor.

Homologa vertikaler och vinklar

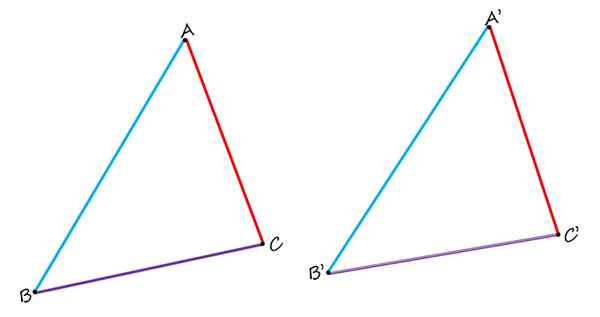
Liksom med sidorna är homologa vertikaler också definierade, som förenar par av homologa sidor. Till exempel är vertikaler A och 'från föregående siffra homologa. På samma sätt är paren av vertikaler B och B 'och C och C' homologa.

Slutligen upptar homologa vinklar samma relativa position i figurerna. Vertikarna med homologa vinklar är i sin tur homologa.

För att illustrera idén, ta vinkeln mellan de blå och lila sidorna på den vänstra triangeln, som kan betecknas som ∠ABC. Denna vinkel har sin motsvarighet i vinkeln ∠A'B'C ', från triangeln till höger.

Vertexen i denna vinkel är B, som som tidigare anges, är en motsvarighet med B ', och de andra två par av homologa vinklar i trianglarna som visas är:

• ∠BCA och ∠B'C'A '
• ∠CAB och ∠C'A'B '

Polygons likhet

För att två polygoner ska vara liknande måste följande förhållanden uppfyllas:

• Alla par homologa vinklar har samma mått
• Hans par homologa sidor är proportionella.

De två villkoren måste uppfyllas samtidigt för att säkerställa likhet. Det observeras omedelbart varför.

I följande figur finns det två fyrkantiga. Det beror på det faktum att den första statusen för Weekly är uppfylld, men den andra gör det inte:

Två fyrkantiga som inte liknar, även om deras homologa vinklar har lika mått. Källa: f. Zapata.

Medan deras siffror i figurerna har homologa vinklar har samma mått, eftersom alla är raka vinklar (de mäter 90º) är figurerna inte lika, eftersom deras sidor inte är proportionella.

Kan tjäna dig: injektiv funktion: vad den består av, vad är det för och exempel

Å andra sidan har dessa två fyrkantiga homologa sidor med lika mått, men de homologa vinklarna mäter inte samma. Därför är siffror uppenbarligen inte liknande.

Två fyrkantiga med homologa sidor av samma mått, men med olika inre vinklar är de därför inte liknande figurer. Källa: f. Zapata.

Likhetsskäl

Om två siffror är liknande är kvoten mellan de homologa sidorna densamma och kallas likhetsskäl.

Betecknar sidorna på en av figurerna som A, B, C, D ... och motsvarande den andra figuren som A ', B', C ', D

Perimetrar och områden med liknande siffror

Likhetsförhållandet möjliggör att få förhållanden mellan perimetrar, områden och volymer av två liknande siffror.

Omkretsskäl för två liknande siffror

Omkretsen P för en polygon definieras som summan av alla sidor. Om du har en figur vars sidor är en ', b', c ', d' ... är dess omkrets P ':

P '= a' + b ' + c' + d '.. .

Om en annan polygon liknar detta, och dess sidor är A, B, C, D ..., är det uppfyllt att:

Och därför:

A = r ∙ a '

Du kan bekräfta samma sak för de andra sidorna av denna figur. Så omkretsen P uttrycks som:

P = A + B + C + D .. . = R ∙ A ' + R ∙ B' + R ∙ C ' + R ∙ D' + ..

Eftersom "r" är en vanlig faktor för alla missbrukare är förhållandet mellan p och p ':

P = r ∙ p '

Detta innebär att orsaken till omkretsen mellan två liknande polygoner är lika med orsaken till likhet.

Anledning till områden med två liknande siffror

Om två liknande siffror har områden A och A ', är dessa relaterade genom:

Kan tjäna dig: Formel Clearance -övningar

A = r²∙ a '

Där "r" är orsaken till likheten mellan siffrorna.

Volymförhållandet på två liknande siffror

De är två liknande tre dimensionella figurer, vars volymer är respektive V och V '. Förhållandet mellan dem, genom "R" är:

V = r³∙ V '

Exempel

Ritning

Delar av ett land, anläggningen i en byggnad eller till och med ett plagg, i mindre skala på ett pappersark kan representeras. Planerna har fördelen av att kunna ta med sig och göra de relevanta modifieringarna lätt innan de genomförs på det verkliga objektet.

Kartor

De är vanligtvis representationer i planet för ett stort landområde, från en by till kontinenterna. De görs också i en viss skala.

De har många applikationer och det finns många typer. Till exempel, genom en karta kan terrängen beskrivas, och när den är belägen på en specifik punkt bestäms den bästa vägen att gå från den punkten till en annan.

Modeller

De är tre dimensionella representationer i skalan av föremål som bilar, byggnader och konstruktioner i allmänhet.

Träning löst

Följande värden motsvarar sidorna på ett par liknande trianglar. Hitta orsaken till likhet och värden på "X" och "Y":

Triangel 1: 5, 8, 10

Triangel 2: 150, x, y

Lösning

Anledningen till likhet är kvoten:

R = 150/5 = 30

Därför:

x = 30 × 8 = 240

y = 10 × 30 = 300