Ampère formel och ekvationer lag, demonstration, övningar

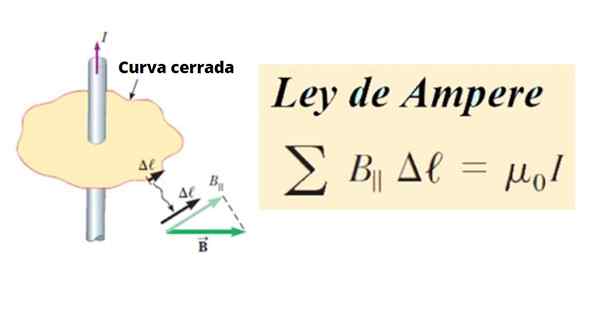
De Ampère lag säger att cirkulationen av den magnetiska induktionsvektorn B Det är proportionellt mot intensiteten och strömmen som flyter med samma.

I sin tur cirkulationen av B Det är summan av alla produkter mellan tangentialkomponenten B_║ och längden på ett litet segment Δℓ av en stängd kurva c, Runt en krets. I matematiska termer är det skrivet så här:

∑ B_║ .Δℓ ∝ Yo

Figur 1. Definition av Ampere -lagen. Källa: Serway, R. Högskolefysik.

Som en godtycklig linje eller kurva kan den delas upp i små segment Δℓ, Och dessa i sin tur kan vara oändliga, då kallas de Dℓ.

I detta fall blir summan en integrerad linje för den skalära produkten mellan vektorerna B och Ds. Denna produkt innehåller den tangentiella komponenten i B, som är b cosθ, där θ är vinkeln mellan vektorerna:

Den lilla cirkeln som korsar integralen innebär att integration utförs på en stängd bana C, som i detta fall innebär att strömmen flyter genom förarens tvärsnitt.

Proportionalitetskonstanten som är nödvändig för att fastställa jämlikhet är μ_antingen, Vakuumpermeabilitet. På detta sätt kvarstår Ampères lag:

Ampères lag berättar för oss att linjen integrerad ∫_C B ∙ Ds Det är värt exakt μ_antingenJag, men det erbjuder oss inte detaljerna om hur magnetfältet är orienterat B När det gäller kurva C vid varje punkt, eller hur man beräknar integralen. Det säger bara att resultatet av samma alltid är μ_antingenYo.

[TOC]

Demonstration av Ampères lag

Ampères lag är verifierad experimentellt kontrollera magnetfältet som produceras av en mycket lång rätlinjig ledare. Innan problemet tar upp problemet måste två fall av särskilt intresse för den tidigare ekvationen lyfts fram:

Det kan tjäna dig: lysande kroppar: egenskaper och hur de genererar sitt eget ljus

-Den första är när B och Ds De är parallella, vilket betyder det B är tangentiellt för c. Då är vinkeln mellan båda vektorerna 0º och den skalära produkten är helt enkelt produkten av storleken B.ds.

-Den andra inträffar om B och Ds De är vinkelräta, i vilket fall är skalprodukten 0, eftersom vinkeln mellan vektorerna är 90º, vars kosinus är 0.

En annan viktig detalj är valet av kurva c på vilken fältcirkulationen utvärderas. Ampères lag anger inte vad den kan vara, men den måste packa in den nuvarande distributionen. Det säger inte heller hur man reser kurvan och det finns två möjligheter för detta.

Lösningen är att tilldela skyltar enligt rätt tumregel. De fyra fingrarna är böjda i den riktning du vill integrera, vanligtvis kommer detta att vara detsamma i fältet B cirkulera. Om de nuvarande punkterna i riktning mot höger tumme, tilldelas ett skylt och om inte, tecken -.

Detta gäller när det finns en fördelning med flera strömmar, vissa kan vara positiva och andra negativa. Den algebraiska summan av dem är vad vi kommer att placera i lagen om Ampère, som vanligtvis utses som Otorns ström (För kurvan c).

Magnetfält av rätlinjen och oändlig tråd

Figur 2 visar en tråd som transporterar en ström och ut ur planet. Den högra tumregeln säkerställer det B Det cirkulerar i motsatt riktning och beskriver omkretsar som de röda pilarna visar.

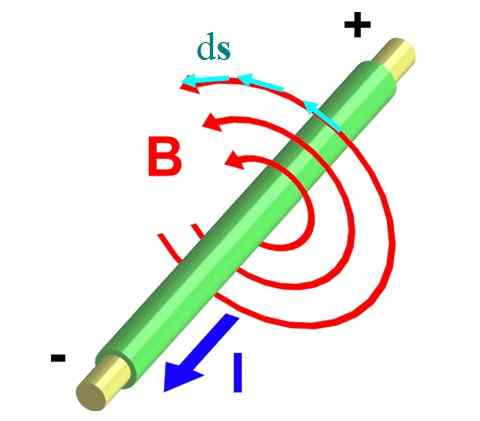figur 2.- Magnetfält i en oändlig tråd. Källa: Wikimedia Commons.

Låt oss ta en av dem, vars radie är r. Vi delar upp det i små differentiella segment ds, representerad med hjälp av blå vektorer. Båda vektorerna, B och Ds, De är parallella vid varje punkt i omkretsen, och på detta sätt den integrerade ∫_C B ∙ Ds Det förvandlas i:

Kan tjäna dig: likström

∫_C Bds

Detta beror på att, som vi sa tidigare, den skalära produkten B ∙ Ds  Det är produkten av vektors storlekar av 0º -kosinusen. Resultatet av integralen är känd tack vare Ampères lag, därför skriver vi:

∫_C BDS = μ_antingenYo

Eftersom fältets storlek är konstant över hela banan lämnar det integralen:

B ∫_C DS = μ_antingenYo

Den integrerade ∫_C DS representerar summan av alla oändliga segment som utgör radioomkretsen r, Motsvarande dess längd, produkten av sin radie med 2π:

B.2πr = μ_antingenYo

Och därifrån upptäcker vi att storleken på B är:

B = μ_antingenI / 2πr

Det är nödvändigt att betona att även om den valda banan (eller Amperian Circuit) Inte cirkulär, resultatet av den integrerade fortsätter att vara μ_antingenJag, men ∫_C B ∙ Ds Det skulle inte längre vara b.2πr.

Det är därför användbarheten av Ampères lag att bestämma magnetfältet ligger i att välja fördelningar med hög symmetri, så att integralen är lätt att utvärdera. Cirkulära och rätlinjiga banor uppfyller detta krav.

Löst övningar

- Övning 1

Överväg kurvor A, B, C och D som visas i figur 3. De lindrar tre strömmar, två som lämnar planet, symboliserat med en punkt ( . ), vars intensiteter är 1 A och 5 A, och en ström som kommer in i planet, som betecknas med ett kors och vars storlek är 2 A.

Hitta den nuvarande inneslutna av varje kurva.

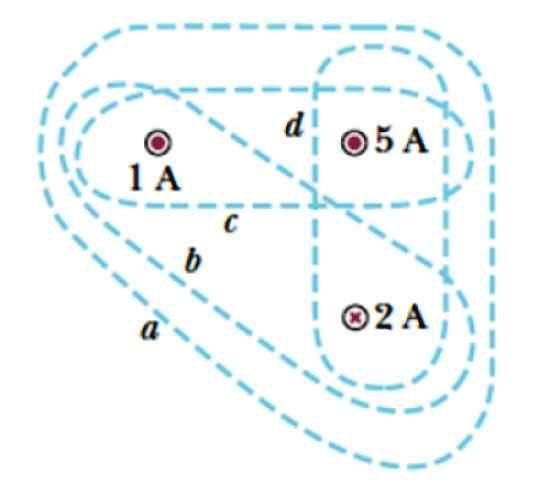Figur 3. Flera kurvor för att tillämpa Ampères lag. Källa: Serway, R. Högskolefysik.

Lösning

Strömmarna som lämnar papperet tilldelas ett skylt +. Enligt det här:

Det kan tjäna dig: ytliga vågor: egenskaper, typer och exempel

Kurva a

Omsluter de tre strömmarna, därför är den slutna strömmen + 1 a + 5 a - 2 a = 4 a.

Kurva B

Endast strömmarna på 1 a y - 2 a är inuti denna kurva, därför är den slutna strömmen från - 2 a.

Kurva c

Innehåller de utgående strömmarna 1 och 5 A, därför är den slutna strömmen 6 a.

Kurva D

Strömmarna inuti är +5 a och - 2 a, och omsluter sedan en nettoström på 3 till.

- Övning 2

Beräkna magnetfältets storlek som produceras av en mycket lång rätlinjig tråd.

Lösning

Enligt Ampères lag ges trådfältet av:

B = μ_antingenI / 2πr = (4π x 10^-7 x 1/2π x 1) t = 2 x 10^-7 T.

Referenser

1. Figueroa, D. (2005). Serie: Physics for Science and Engineering. Volym 6. Elektromagnetism. Redigerad av Douglas Figueroa (USB).
2. Riddare, r.  2017. Fysik för forskare och teknik: En strategistrategi.  Pearson.
3. Sears, Zemansky. 2016. Universitetsfysik med modern fysik. 14th. Ed. Volym 2.
4. Serway, R. 2009. Högskolefysik. Cengage Learning.
5. Tipler, s. (2006) Fysik för vetenskap och teknik. 5: e upplagan. Volym 2. Redaktör.