Darcylag

Vi förklarar vad som är Darcys lag, dess ekvationer, tillämpningar, begränsningar och föreslår en övning som ska lösas

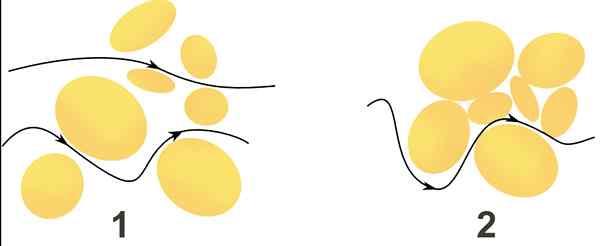
Vattenflöde genom två porösa medier indikeras genom svarta pilar. I medium 1 rör sig flödet snabbare än i mitten 2, eftersom hastigheten beror på storleken på mellanrummen och enkel kommunikation mellan dem. Källa: Wikimedia Commons.

Vad är Darcys lag?

De Darcylag Det är en matematisk relation som är tillämplig på flödet av vätskor i permeabla eller porösa medier, till exempel vattnet som dränerar i sanden.

När vätskan går framåt genom det porösa är dess hydrostatiska tryck varierande, särskilt det är större vid de punkter som är närmast källan och lägre vid de punkter som är närmast dränering. På detta sätt visas begreppet hydraulisk gradient, en fysisk mängd som kommer att betecknas med bokstaven i.

Å andra sidan kännetecknas det porösa mediet av ett belopp som heter Hydraulisk konduktivitet K. Det finns helt klart en relation mellan porositeten, bestämd av K, den hydrauliska gradienten I och flödet per enhet av tvärsnitt Q Q Q.

Förhållandet mellan dem upptäcktes av den franska hydrauliska ingenjören Henry Darcy (1803-1858), som var ansvarig för vattenförsörjningen i sin hemstad: Dijon.

Darcys lag presenterades 1856, i ett grundligt arbete där de fysiska mängderna som är involverade i lagen är detaljerade, experimenten genomfördes och särskilt särskilt en apparat som kallas permeemeter.

Darcy lagekvationer

Darcys lag visar förhållandet mellan flera fysiska mängder som beskriver flödet genom ett poröst medium. Det indikerar att vattenflödet Q som rör sig genom ett visst poröst medel är direkt proportionell mot tvärsnittet genomborrade till och den hydrauliska gradienten Yo:

Q ∝ A ∙ i

Kan tjäna dig: enhetlig rätlinjig rörelse: egenskaper, formler, övningar

Proportionalitetskonstanten är permeabiliteten k för den porösa miljön, även kallad Hydraulisk konduktivitet. På detta sätt presenteras Darcys lag som:

Q = k ∙ a ∙ i

Differentialform av Darcys lag

Darcys ekvation kan uttryckas som ett differentiellt samband mellan flödeshastigheten vid varje punkt och den lokala hydrauliska gradienten:

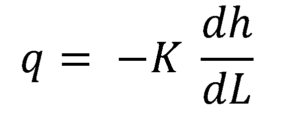
Eftersom den hydrauliska gradienten är en negativ mängd när den beräknas i flödesriktningen är det då nödvändigt att multiplicera med det negativa av hydraulisk konduktivitet för att erhålla medelflödeshastigheten Q, i varje tvärsnitt.

Sedan analyseras storleken i Darcys lag mer detaljerad.

Flöde, hydraulisk gradient och permeabilitet

1.- Flöde q

Flödet definieras som vattenvolymen som cirkulerar genom ett visst tvärsnitt till flödesriktningen, per tidsenhet:

Q = ΔV / ΔT

I det internationella systemet med SI -enheter mäts flödet på kubikmeter per sekund, men det uttrycks ofta i liter per minut eller liter per sekund.

Flödet per enhet i Q -området krävs ofta, vilket är förhållandet mellan Q -flödet och tvärsnittet:

Q = Q / A

I SI uttrycks Q i M/S, varför Q representerar vätskans medelhastighet i rörets tvärsnitt.

Det är viktigt att notera att även om flödet Q är detsamma i alla delar av röret, är flödet per enhet i arean Q eller helt enkelt flödeshastigheten högre i de smalaste och mindre sektionerna i det bredare.

2.- Hydraulisk gradient i

När en vätska cirkulerar längs ett poröst medium minskar hydrostatisk tryck i samma riktning för flödet.

Kan tjäna dig: ton: transformationer, ekvivalenser och övningar löst

Det är känt att det hydrostatiska trycket, vid en viss punkt i röret, är proportionell mot höjden h som markerar en öppen rörtrycksmätare på den platsen. Proportionalitetskonstanten är produkten av vätsketäthet på grund av tyngdkraftsacceleration.

På detta sätt definieras den hydrauliska gradienten I som förhållandet mellan höjdskillnaden ΔH för kolumnerna för två manometrar och ΔL, den senare är avståndet som skiljer manometrarna (se figuren nedan):

I = ΔH / ΔL

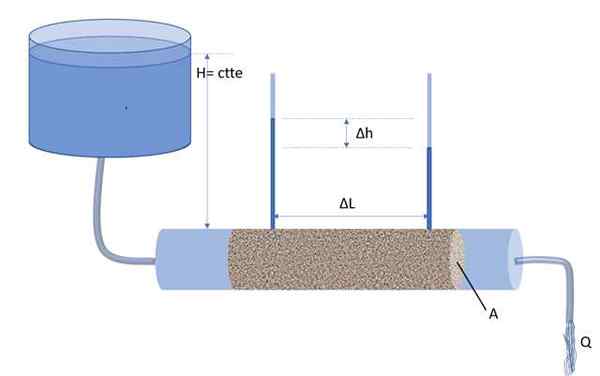Permemetern, en apparat uppfann av Henry Darcy för att kvantifiera vattenflödet genom ett poröst medium. Källa: f. Zapata.

Detta är den genomsnittliga hydrauliska gradienten i sektionen av Long ΔL, en dimensionslös mängd och också negativ.

Om du vill hitta den hydrauliska gradienten vid varje punkt i röret, tas gränsen för ΔL tending till noll, vilket resulterar i derivatet av den hydrauliska gradientfunktionen med avseende på position L, längs flödet:

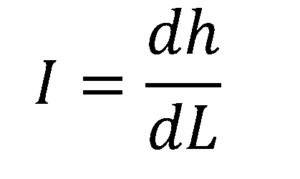
3.- Permeabilitet k

Permeabiliteten för ett poröst medel eller hydraulisk konduktivitet är förhållandet mellan flödet Q och produkten från tvärsnittet TILL För den hydrauliska lutningen Yo:

K = q / a ∙ i

Hydraulisk konduktivitet har hastighetsenheter, mätare över sig själv.

En enhet för k har definierats, kallas Darcy, För att hedra Henry Darcy och definieras på följande sätt:

En Darcy Det är permeabiliteten hos en flytande milliliter, med en viskositet av en centipoise, som rör sig längs en centimeter i ett differentiellt tryck i en atmosfär, genom ett tvärsnitt av en fyrkantig centimeter.

Darcy Law Applications

Den huvudsakliga tillämpningen av Darcys lag är att förutsäga vattenflödet längs en akvifer, innan du borrar brunnar.

Kan tjäna dig: dimensionell analys

Darcys lag används också regelbundet inom jordbruks- och hydrologisk teknik. Det kan också användas i oljeindustrin för att beskriva flödet av gas och olja i porösa medier. I så fall kan K emellertid variera beroende på flödet av gas eller olja och kanske inte är beroende av det permeabla underlaget.

Begränsningar

Darcys lag antar att den hydrauliska konduktiviteten k är en mängd av mediet, vilket är sant i många fall. Ibland beror ibland k på vätskans dynamiska viskositet, som i sin tur kan bero på flödeshastigheten och temperaturgradienterna.

Darcys antagande är troligt när man överväger underjordiskt vatten, där viskositeten är praktiskt taget konstant, eftersom dess värde nästan inte påverkas med tanke på de få temperaturskillnaderna i hela akvifer.

I fall av oljeflöde genom porösa medel kan Darcy -ekvationen inte tillämpas som presenteras här, men vissa modifieringar är införlivade som går utöver syftet med denna artikel.

Träning löst

Bestäm den hydrauliska konduktiviteten hos en strandsand genom att använda en laboratoriepermeter.

Anta att permemeterröret har en diameter på 20 cm och att avståndet mellan de två manometrarna är 50 cm. Det är också känt att vattenflöden med en hastighet av 300 kubik decimetrar per minut och nivånskillnaden mellan de två manometrarna är 25 cm.

Lösning

Flödet som är 300 kubiska decimeter per minut, men uttrycker i enheter i det internationella systemet skulle det vara så här:

Q = 300 x 10^-3 m³ / 60 s = 5 x 10^-3 m³ / s

Tvärsnittet A beräknas av:

A = π ∙ r² = π ∙ (10 cm)² = π ∙ (0,1 m)² = 0,314 m²

Hydraulisk gradient I är en kvot mellan den manometriska höjdskillnaden och separationen av manometrarna:

I = 25 cm / 50 cm = 0,5

Enligt definitionen av hydraulisk konduktivitet K som anges ovan:

K = q / a ∙ i = (5 x 10^-3 m³ / s) / (0,314 m² ∙ 0,5) = 3,185 x 10^-2 m/s ≈ 2 m/min.