Ficks lag

Vad är Ficks lag?

De Ficks lag Det är en matematisk ekvation som relaterar massflödet spridd i ett medium med koncentrationer eller tryckgradient. Det formulerades 1855 av den tyska fysiologen och läkaren Adolf Fick, som inspirerades av Fouriers lagar (termisk ledning) och OHM (elektrisk ledning), modellerade processen för diffusion av syre till lungans alveoler.

Ficks lag presenterar specialiteten att den inte bara är tillämplig på kemiska eller biokemiska diffusionsfenomen, utan på alla slags natur. Därför tjänar det till att modellera spridningen av atomer mellan fasta ämnen, är mycket användbar i fysiken för material och teknik.

Representation av en diffusionsprocess genom ett semipermeabelt membran. Källa: Gabriel Bolívar.

Men den centrala basen är densamma för nästan alla diffusionsfenomen, som illustreras ovan. Lila partiklar, vara atomer eller molekyler, sprids genom ett semipermeabelt tjockt membran L och tvärgående område till. Till vänster har vi en större koncentration c₁ av partiklar som till höger, c₂.

Ficks lag fastställer följande: Massflödet som sprids genom en yta är proportionell mot koncentrationsgradienten (C₂-C₁/L) och en konstant D som kallas diffusion eller diffusivitetskoefficient.

Denna lag har två former: en baserad på rymden (x), och en annan beroende på utrymme och tid (x, t). Den första gäller för system i stationära förhållanden, medan den andra för verkliga, icke -stationära system.

Ficks första lag

Komponenter och ekvation

Det tjocka L för det semipermeabla membranet representerar avståndet (x) som partiklarna måste resa för att nå andra sidan. Som framgår av bilden, lila partiklar ju mer de rör sig bort från det vänstra facket, där c₁ Det är bra, dess koncentration minskar till värdet på C₂. Det vill säga koncentrationen förändras längs membranets tjocklek och är beroende av x.

Denna koncentrationsvariation beroende på avstånd är det som kallas koncentrationsgradient: (c₂-C₁)/L o (c₂-C₁)/x. Observera att dess värde är negativt (-1), eftersom c₂ > C₁.

Å andra sidan har vi också den hastighet som partiklarna sprids genom membranet eller det aktuella utrymmet. Denna hastighet beror på partiklarnas storlek och massa, liksom miljön och temperaturen. Diffusionskoefficienten D representerar denna hastighet och kan vara konstant eller inte under diffusion.

Kan tjäna dig: laboratoriefilter): egenskaper, funktioner, typer

Och slutligen har vi ett massflöde 'J' som korsar det tvärgående området på membranet eller kanalen där partiklarna sprids. Genom att gruppera dessa termer föds ekvationen för Ficks första lag:

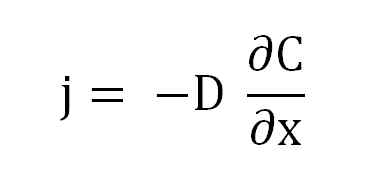Ekvation av Ficks första lag. Källa: Gabriel Bolívar.

Där J är proportionell mot D och A (∂c/∂x), koncentrationsgradienten.

Tolkning och enheter

Den negativa symbolen i ekvationen tjänar till att neutralisera det negativa tecknet på koncentrationsgradienten. Annars skulle J ha ett negativt värde, som är oinhupered. På samma sätt är värdet på d positivt, så att genom att multiplicera med det negativa tecknet som föregår det ger det ett negativt värde.

Ficks första lag indikerar följande: ju större koncentrationsgradienten (∂c/∂x), desto större är massflödet J. Det vill säga skillnaden mellan C₂ och C₁ Det blir större och därför kommer fler partiklar att spridas genom membranet.

Å andra sidan beror J också på D, som i sin tur är beroende av parametrar som temperatur, viskositet, molekylvikt och det tvärgående området till:

D ∝ (a/l) (s/√m_W)

Där s är lösligheten för partikeln som är spridd med miljön och m_W Dess molekylvikt.

När det gäller enheterna i komponenterna eller termerna i ekvationen vi har:

-C (kg · m^-3 eller mol · m^-3)

-D (m^-2·^-1)

-J (kg · m^-2·^-1 eller mol · m^-2·^-1)

Netto medium kvadratisk förskjutning

Under spridningen kolliderar partiklarna med varandra, och efter korta tidsintervall reser de enorma avstånd Δx. Beroende på betydelsen av dessa förskjutningar kan Δx emellertid ha negativa eller positiva värden (enligt en ursprungspunkt). Det är därför genomsnittet av Δx -värdena för alla molekyler tenderar att 0.

Å andra sidan är Δx -värdena mycket små jämfört med de avstånd som kör partiklarna. När de kolliderar förlorar de rörlighet mot en riktning och har följaktligen en begränsad nettoförskjutning; Till exempel 2 cm framsteg i en riktning efter att ha resat hundratals meter i kollisioner och returer.

Einstein 1905 fann ett matematiskt uttryck för förskjutningens genomsnittliga rullning (därför skiljer sig från 0):

<(Δx)²> = 2dt

Definierande

(Δx)_Rms ≡ '16ter'. '.' <(Δx)²>^1/2 = (2dt)^1/2

(Δx)_Rms Det är den genomsnittliga netto kvadratiska förskjutningen av partiklarna i fråga. (Δx)_Rms Det berättar hur mycket partiklar rör sig i genomsnitt (i en positiv eller negativ riktning) enligt tiden. Vissa partiklar kommer att röra sig längre eller närmaste avstånd än (Δx)_Rms, orsakar en Gaussisk distribution.

Kan tjäna dig: kalciumoxid (CAO)

Fick andra lag

Ekvation

Ficks första lag beskriver diffusionen i stationära förhållanden, det vill säga massflödet J varierar inte över tid. I verkliga system har vi emellertid icke -stationära förhållanden, där massflödet inte bara varierar i rymden, utan också med tiden. Därför är den intresserad av att bestämma (∂c/∂t).

Nedan har vi två ekvationer som representerar Ficks andra lag:

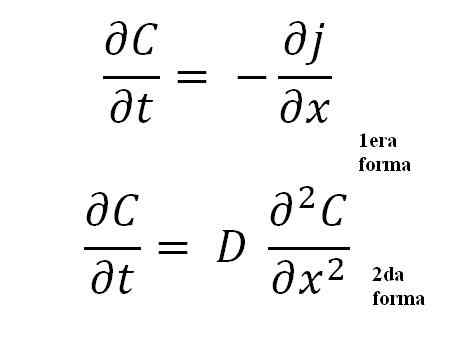Ekvationer av Ficks andra lag. Källa: Gabriel Bolívar.

Den andra formen är den viktigaste av alla, eftersom den representerar den allmänna matematiska ekvationen för varje spridningsprocess; Antingen termisk, elektrisk, atom, etc.

Avdrag

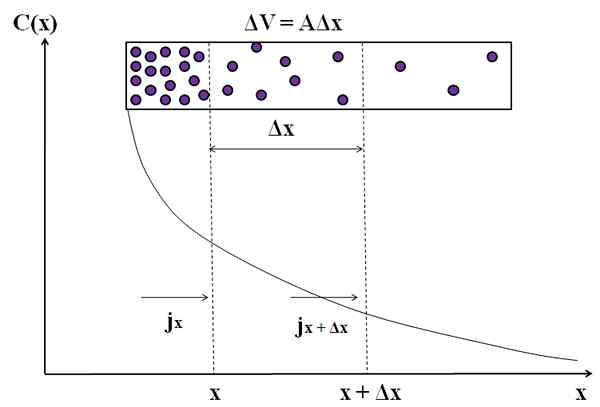Grafisk representation av hur massflödet inte är konstant i spridningen av dessa molekyler. Källa: Gabriel Bolívar.

Tänk igen lila partiklar i en rektangulär kammare. Bland avståndet x och x+Δx har vi ett flöde j_x (inkommande) och J_x+Δx (Utgående). Volymen på kameran mellan dessa avstånd definieras av:

ΔV = aΔx

Observera att graf C (x) vs x inte har sitt ursprung i en rak linje, så vi har olika värden på j (j_x ≠ j_x+Δx). Vi måste bestämma ΔC/ΔT.

Massan m_x Det kommer att vara lika med:

m_x = J_x AΔt

En dimensionell analys hjälper till att förstå varför:

kg = (kg · m^-2·^-1) (m²) (S)

På samma sätt beräknar vi M_x+Δx:

m_{x+ Δx} = J_x+Δx AΔt

Att vara massan som ackumuleras i den regionen som är lika med Δm:

Δm = m_x - m_{x+ Δx}

= (j_x - J_{x+ Δx}) AΔt

= -(j_{x+ Δx} - J_x) AΔt

= -ΔJAΔT

Och att veta att ΔC = Δm/ΔV

ΔC = -ΔJAΔT/ ΔV

= -ΔjaΔt /aΔx

= -ΔjΔt/Δx

Vi rensar ΔC/ΔT

ΔC/Δt = -Δj/Δx

Detta uttryck indikerar att variationen i koncentrationen över tid är lika med variationen i J -flödet med avseende på dess förskjutning. Tillämpa gränserna för Δt och Δx tending till 0 får vi samma uttryck som ett partiellt derivat:

∂c/∂t = -(∂j/∂x) (1: a formulär)

Slutligen erhålls den andra formen genom att ersätta J med Ficks första lag:

∂c/∂t = -∂/∂x (-d∂c/∂x)

= D (∂²C/∂x²) (2: a formen)

Löst övningar

I följande övningar kommer mycket enkla system att betraktas vars okända kan lösas med Ficks första lag.

Övning 1

Påstående

I ett rör 15 meter långt och 21 centimeter brett, och som också är mättat med kväve, sprids en syreström från ena änden till en annan vid en temperatur av 0 ºC. Att veta att trycket på vänster sida (P₁) är 20 kg/m³, Och att trycket på höger sida (P₂) är 10 kg, bestäm:

Det kan tjäna dig: hydroniojon

a) Massflödet som sprids

b) hur många kilo eller₂ De kommer att spridas genom röret på 17 minuter?

c) koncentrationsgradienten eller trycket

d) trycket från O₂ på ett avstånd av 7 meter från ingången till rörledningen

e) hur mycket kommer 80 kg o₂ I spridning genom detta rör?

Tänk på att D_O2-n2 är lika med 1.8 · 10^-5 m²·^-1.

Upplösning

Från Ficks första lag måste vi lösa underavsnitt A):

J = -d (p₂-P₁)/L

= -(1.8 · 10^-5 m²·^-1) (10-20) (kg/m³)/(15 m)

= 1.2 · 10^-5 kg · m^-2·^-1

Till B) Vi behöver rörområdet:

A = π (0.21 m)²

= 0.14 m²

Och vi multiplicerar J med A och Time T för att bestämma massan av eller₂ Utrustat:

m_O2 = (1.2 · 10^-5 kg · m^-2·^-1) (17 s) (0.14 m²)

= 3.57 · 10^-5 kg

Nu, för underavsnitt c) har vi att lutningen är lika med:

Lutning = (P₂-P₁)/L

= (10-20) (kg/m³)/15 m

= -2/3 (kg/m³) · M^-1

Men vi tar det positiva värdet, vilket är fysiskt vettigt:

2/3 (kg/m³) · M^-1

Detta värde kommer sedan att tjäna oss för att lösa underavsnittet d) om lutningen tolkas väl: varje mätare trycket på eller₂ 2/3 kg/m kommer att falla³. Genom att sprida 7 meter kommer vi att ha:

2/3 (kg/m³) · M^-1 (7 m) = 14/3 eller 4.7 kg/m³

Det vill säga trycket på det avståndet kommer att vara:

(20-4.7) (kg/m³) = 15.3 kg/m³

Och slutligen är underavsnitt E) lik B), bara att vi nu rensar tid och inte massan:

m_O2 = Jat

t = m_O2/Ja

= (80 kg)/(1.2 · 10^-5 kg · m^-2·^-1) (0.14 m²)

= 47619.04 s eller 0.55 dag

Övning 2

Påstående

Bestämma (Δx)_Rms För sackaros i vatten vid t = 1 min, 1 timme och 1 dag. Spridningskoefficienten för sackaros i vatten är 0.52 · 10^-5centimeter²·^-1.

Upplösning

Vi tillämpar ekvationen:

(Δx)_Rms ≡ '16ter'. '.' <(Δx)²>^1/2 = (2dt)^1/2

Vi utvärderar (Δx)_Rms Med tiderna uttryckta på några sekunder. För t = 1 min eller 60 s:

(Δx)_Rms = ((2 (0.52 · 10^-5centimeter²·^-1) (60s))^1/2

= 0.025 cm

För t = 1 h eller 3600 s:

(Δx)_Rms = ((2 (0.52 · 10^-5centimeter²·^-1) (3600S))^1/2

= 0.19 cm

Och slutligen för t = 1 dag eller 86400 s:

(Δx)_Rms = ((2 (0.52 · 10^-5centimeter²·^-1) (86400S))^1/2

= 0.95 cm

Observera att när tiden går har sackarosmolekylerna inte ens kunnat flytta 1 cm i några riktningar.

Referenser

1. Walter J. Moore. (1963). Fysisk kemi. I kemisk kinetik. Fjärde upplagan, Longmans.
2. Iran. Levin. (2009). Principer för fysikalik. Sjätte upplagan. MC Graw Hill.
3. Introduktion till materialvetenskap och teknik. (11 mars 2018). Ficks andra lag. Prof. Rajesh Prasad. [VIDEO]. Återhämtat sig från: YouTube.com
4. Wikipedia. (2020). Ficks diffusionslagar. Hämtad från: i.Wikipedia.org
5. Laura Dickson. (10 september 2020). DIFFUSION. Kemi librettexts. Återhämtad från: kem.Librettexts.org
6. Larissa Zhou et al. (1 september 2015). Förstå diffusionsteori och Ficks lag genom mat och matlagning. American Physiologic Society. doi.org/10.1152/Advan.00133.2014