Tecken lag

Vi förklarar teckens lag, med exempel och övningar löst

SCHEME OF TILLÄGGNINGAR

Vad är teckens lag?

De Tecken lag Det är uppsättningen av regler som används i aritmetiska och algebraiska beräkningar med verkliga siffror för att korrekt tilldela tecknet till resultatet, när både positiva och negativa mängder är involverade.

Det finns tillräckliga regler enligt operationen som utförs: summa, subtraktion, multiplikation och uppdelning, som är de mest grundläggande, och det finns också regler för tecken relaterade till potentiering och arkiveringsoperationer.

I en given operation, vare sig det är för hand eller med kalkylator, är det nödvändigt att korrekt tillämpa lagen om skyltarna för att säkerställa ett korrekt resultat, eftersom bara en liten förändring i tecknen avsevärt förändrar beloppen.

Lagen om tecknen för varje grundläggande aritmetisk operation och de fall som kan uppstå undersöks nedan.

Lag om skyltar i summan

1) Om siffrorna ska läggas har samma tecken

Siffrorna läggs till som vanligt och resultatet läggs till tecknet på siffrorna, oavsett om detta är positivt eller negativt.

Det är viktigt att komma ihåg att positiva siffror vanligtvis inte är före skylten, men skrivs direkt. Å andra sidan skrivs negativa siffror inom parentes, särskilt när de föregås av symbolen för en aritmetisk operation för att undvika förvirring.

Exempel på summor med samma tecken:

3 + 9 = 12
4 + 7 + 1 + 6 = 18
(−3) + (−8) = −11
(−5) + (−10) + (−6) = −21

2) Om siffrorna ska läggas har olika tecken

Siffrorna subtraheras och tecknet på antalet som har det största absoluta värdet läggs till resultatet, vare sig det är positivt eller negativt.

Som ett exempel, genomföra operation 5 + (−14). Eftersom det absoluta värdet på (−14) är större än det absoluta värdet på 5, dras 5 enheter från 14, vilket ger 9 och detta resultat placeras negativt tecken:

Kan tjäna dig: prismor och pyramider

5 + (−14) = −9

Fler exempel på denna regel som tillämpas på summan av två antal olika tecken är:

(−27) + 12 = −15

12 + (−7) = 5

Om det finns mer än två tillägg med olika tecken i operationen Summan associerande egendom:

(−20) + 9 + (−7) = [(−20) + 9] + (−7)

Operationen utförs först i Pracete, som består av summan av två antal olika tecken, för vilket den beskrivna regeln tillämpas: resultatet subtraheras och tecknet på antalet med det högsta absoluta värdet:

(−20) + 9 = −11

Operationen är så här:

(−20) + 9 + (−7) = (−11) + (−7)

Nu har du summan av två nummer av samma tecken, sedan läggs de normalt till och resultatet placeras ett negativt tecken:

(−20) + 9 + (−7) = (−11) + (−7) = −18

Tecken i ersättaren

Subtraktionen av två siffror definieras som summan av det motsatta. I sin tur sägs motsatsen till ett nummer nummer med det ändrade tecknet. Till exempel är motsatsen till 2 (−2), motsatsen till (−5) är 5 och så vidare.

Med detta i åtanke, när du har subtraktionen av två nummer:

A - B

Det förvandlas helt enkelt till summan av motsatsen till B:

A + ( - b)

Och fortsätt som beskrivs i föregående avsnitt. Anmärkning för att sätta ett tecken + ett negativt nummer förändrar inte det, men mycket försiktigt, det motsatta är inte sant.

När antalet "A", som är minuend, är större än antalet "B", som är stulen, fungerar som i subtraktionen av naturliga siffror. Inga problem, eftersom ett stort antal dras från ett mindre belopp:

Kan tjäna dig: ojämlikheten i triangeln: demonstration, exempel, lösta övningar

25 - 8 = 17

Med följande exempel är metoden att lägga till det motsatta av subtrahera mycket bekvämt:

(−5) - 24 = (−5) +( - 24) = - 29
32 - (−23) = 32 + 23 = 55

Lag om skyltar i multiplikation

Lagen om tecknen i multiplikation tillämpas på detta sätt:

• Genom att multiplicera två nummer av samma tecken är resultatet alltid positivt.
• Produkten av två motsatta teckennummer är alltid negativ.

Sammanfattningen av teckenregeln för multiplikation visas i bilden:

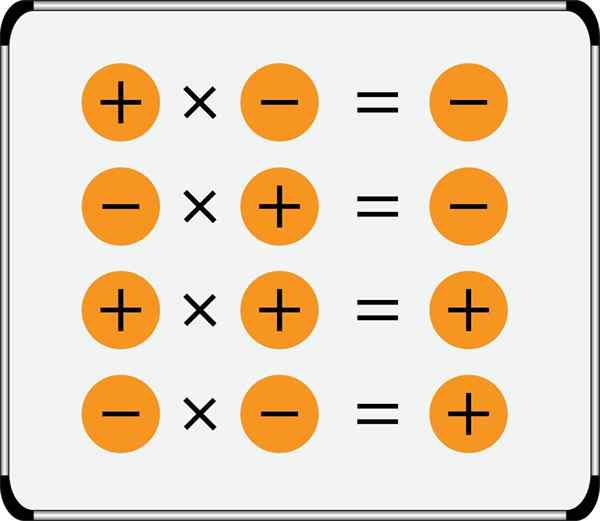
Observera att positiva siffror kan skrivas utan föregående teckna, men negativa siffror har det alltid, dessutom är två aritmetiska symboler aldrig skrivna till varandra, de måste alltid separeras med en parentes, till exempel:

Felaktig: 3 × −4
Korrekt: 3 × (−4) = −12

(−5) × 6 = −5 × 6 = −30
(−3) × (−11) = 33
10 × 27 = 270

För att multiplicera mer än två siffror används den associerande egenskapen för multiplikation, eftersom ordningen på faktorerna inte förändrar produkten, till exempel när du genomför:

(−2) × (−14) × 16

Du kan multiplicera de två första faktorerna, eller de två sista om du vill, och sedan multiplicera resultatet med den återstående faktorn. I det här fallet kommer de två faktorerna att multipliceras först till vänster:

[(−2) × (−14)] × 16

Produkten med två negativa siffror är positiv, sedan (−2) × (−14) = 28 och återstår:

28 × 16 = 448

Lag om skyltar i division

Det är analogt med teckenregeln för multiplikation:

• Förhållandet mellan två siffror av samma tecken är alltid positivt.
• Genom att dela två annars teckennummer är resultatet alltid negativt.

Det kan tjäna dig: skillnad mellan cirkel och omkrets (med exempel)

Till exempel:

24 ÷ 8 = 3
−36 ÷ 3 = −12
162 ÷ (−9) = −18
−216 ÷ (−6) = 36

Lag om skyltar i empowerment och arkivering

En skriftlig nummerexponent är:

tillⁿ

Där "a" är basen och "n" är exponenten. Två fall skiljer sig, enligt exponentens paritet:

Fall 1: A är positiv

När basen är positiv är resultatet positivt oavsett om exponenten är jämn eller udda, som i:

2³ = 8
3⁴ = 81

Fall 2: A är negativt

Här är två fall:

• När exponenten är jämn är resultatet positivt.
• Om exponenten är udda är den negativ.

Exempel

3² = 3 ∙ 3 = 9
2³ = 2 ∙ 2 ∙ 2 = 8
(−2)⁴ = (−2) ∙ (−2) ∙ (−2) ∙ (−2) = 16
(−3)³ = (−3) ∙ (−3) ∙ (−3) = −27

Operationer med gruppsymboler

De visas ofta separata operationer med gruppsymboler: parenteser, parentes och nycklar. Dessa elimineras från insidan och ut med hänsyn till följande:

• Om en gruppsymbol föregås av ett positivt tecken kan den tas bort utan att ändra tecknen på innehållet, till exempel: + (−3 + 5 - 1) = −3 + 5 - 1 = 1.
• Om ett negativt tecken föregår gruppsymbolen dras den tillbaka genom att investera tecknet på innehållet, till exempel: - (−3 + 5 −1) = 3 - 5 + 1 = −1.
• När det finns kombinerade operationer av summa, subtraktion, multiplikation och uppdelning, kan de associativa och distribuerande egenskaperna användas för att bekvämlighet.

Löst övningar

a) 10 + 10

Lösning: 20

b) (-8) + (-3)

Lösning: -11

c) (3) + (-10) 

Lösning: -7

d) (5) x (-3)

Lösning: -15

e) (-10) x (-10)

Lösning: 100

f) (18) ÷ (-3)

Lösning: -6

G) (-10) ÷ (-2)

Lösning: 5

h) 4 - ( - 7 + 9)

Lösning: 4 - ( - 7 + 9) = 4 + 7 - 9 = 11− 9 = 2