Kirchhoff -lag

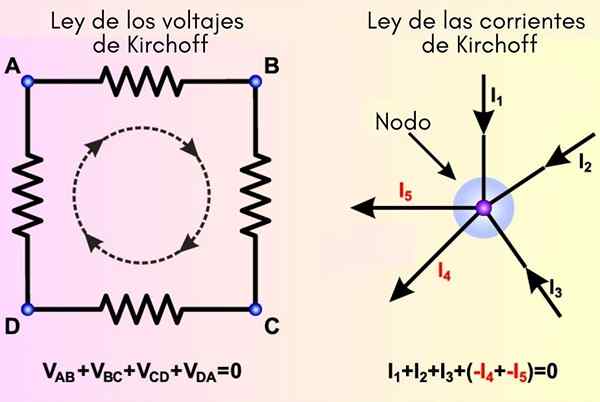
Kirchoffs lagar härstammar från principerna för energi respektive belastning. Till vänster är lagen om meshes etablerad och till höger strömmarna

Vad är Kirchoffs lagar?

De Kirchoff -lag De består av att tillämpa principen om bevarande av den elektriska laddningen och principen om bevarande av energi på de elektriska kretsarna för att lösa de som har flera nät.

Dessa regler, eftersom de inte är lagar i strikt mening, beror på den tyska fysikern Gustav Kirchoff (1824-1887). Användningen är avgörande när Ohms lag inte räcker för att bestämma spänningar och strömmar i kretsen.

Innan uttalandet och tillämpningen av Kirchoffs lagar är det bekvämt att komma ihåg innebörden av några viktiga begrepp på elektriska kretsar:

• Nod: Union Point mellan två eller flera ledande ledningar.
• Gren: Element i kretsen som är mellan två på varandra följande noder, genom vilka samma nuvarande cirkulerar.
• Maska: bana eller sluten slinga består av två eller flera grenar och det reste i samma riktning, utan att gå igenom samma punkt.

Kirchoffs första lag

Det är också känt som lagen om strömmar eller noder, och konstaterar att:

Summan av strömmarna som kommer in i en nod är lika med summan av strömmarna som kommer ut ur den.

Så på ett matematiskt sätt uttrycks den första lagen som:

∑ i = 0

Där symbolen σ indikerar en summa.

Den tidigare ekvationen konstaterar att eftersom den elektriska laddningen inte skapas eller förstörs, måste hela strömmen (belastning per tidsenhet) som kommer in i noden vara lika med den som kommer ut ur den.

Kan tjäna dig: konstgjorda satelliter

Exempel

För att bekvämt tillämpa strömmarna tilldelas ett skylt till de inkommande strömmarna och det motsatta teckenet på de utgående strömmarna. Valet är helt godtyckligt.

Följande bild visar två strömmar som kommer in i en nod, ritad i rött: i₁ och jag₂, och att när de lämnar visas de i grönt: Strömmarna i₃, Yo₄ och jag₅.

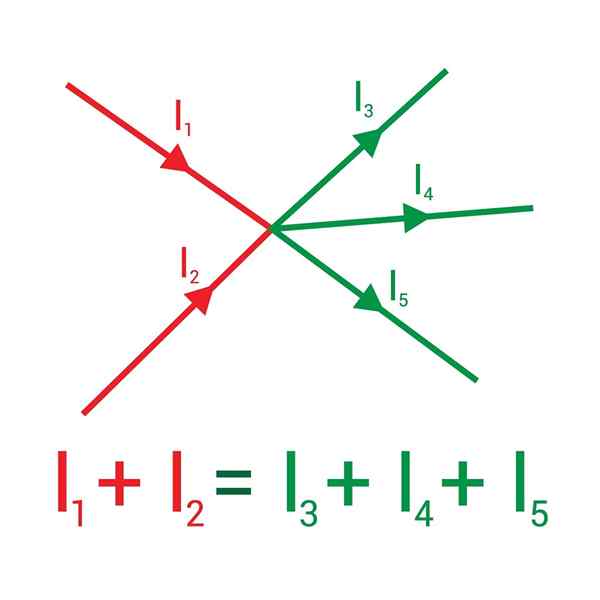Summan av strömmarna som kommer in i en nod är lika med summan av strömmarna som kommer ut ur den

Tilldelar skylten (+) till de inkommande strömmarna och (-) till den utgående, den första regeln om Kirchoff konstaterar att:

Yo₁ + Yo₂ - Yo₃ - Yo₄ - Yo₅= 0 ⇒ i₁ + Yo₂ = Jag₃ + Yo₄ + Yo₅

Kirchoffs andra lag

Andra namn för Kirchoffs andra lag är: Spänningslag, Spänningslag antingen nätlag. I alla fall konstaterar det att:

Den algebraiska summan av spänningsfall längs ett nät är lika med 0.

Detta är ett sätt att tillämpa bevarande av energi i kretsen, eftersom spänningen i varje element är förändringen av energi per lastenhet.

Därför, när du reser en stängd del (ett nät), ökar den algebraiska summan av spänningen och faller 0 och kan skrivas:

∑ V = 0

Exempel

I följande figur har du nätet Abcda, genom vilken en ström cirkulerar i riktning mot klocknålarna och rutten kan börja när som helst i kretsen.

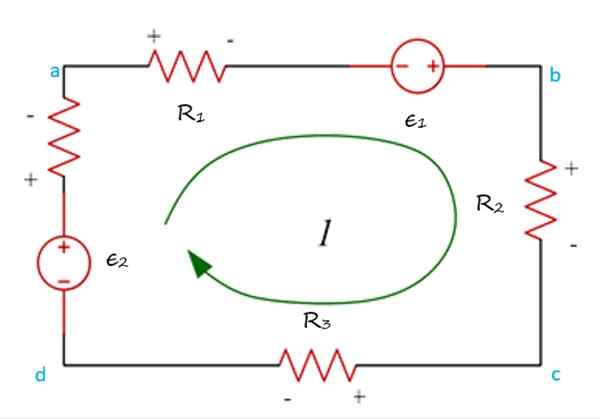Exempel på ett nät turnerade i ett schema, där ökningar och potentiella fall visar sig tillämpa lagen om Kirchoff -spänningarna. Källa: f. Zapata.

Det är också nödvändigt. Det vanliga är att tilldela spänningsökningen som positiv, det vill säga när strömmen cirkulerar från ( -) till (+). Sedan är spänningsfallet, som uppstår när strömmen går från (+) till ( -), negativ.

Kan tjäna dig: kiseloxid (SiO2): struktur, egenskaper, användningar, erhållning

Att starta nätvägen vid punkten "A", är motståndet r₁. I den upplever lasterna en potentiell droppe, symboliserad av skyltarna (+) till vänster och ( -) ovanför motståndet.

Därför spänning eller spänning i r₁ Det har ett negativt tecken.

Sedan når du en direktspänningskälla, kallad ε₁, vars polaritet är mindre (-) Mer (+). Där går de elektriska avgifterna genom en potentiell ökning och denna källa anses vara positiv.

Efter denna procedur för återstående motstånd och den andra källan erhålls följande ekvation som ett resultat:

−V₁ + ε₁ - V₂ - V₃ + ε₂ = 0

Där v₁, V₂ och v₃ är spänningar i motstånd r₁, R₂ och r₃. Dessa spänningar kan hittas från ohms lag: v = i · r.

Träning löst

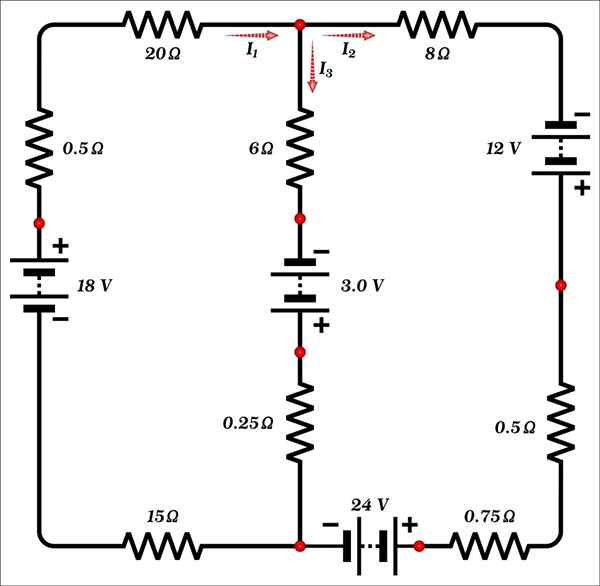
Hitta värdet på strömmar i₁, Yo₂ och jag₃ visas i figuren.

Lösning

Denna krets består endast av två nät och har 3 okända: strömmarna och₁, Yo₂ och jag₃, Så minst 3 ekvationer krävs för att hitta lösningen.

I noden (punkt märkt med rött) som är överst på kretsen på den centrala grenen, observeras att strömmen i₁ är inkommande, medan strömmar i₂ och jag₃ De är utgående.

Därför leder lagen om Kirchoff Currents till den första ekvationen:

1) i₁ - Jag₂ - Jag₃ = 0

Den nedre noden ger samma information, därför är nästa steg att resa meshes.

Första nät

För att fastställa följande ekvation reste nätet till vänster i ett schema, med början från det övre vänstra hörnet. Detta är den mening som strömmar och strömmar cirkulerar₁ och jag₃.

Kan tjäna dig: Optisk komparator: Vad är det för och delar

Anteckna det:

• Yo₁ passerar genom motståndet på 20 Ω, 15 Ω och 0.5 Ω och 18 V -batteriet, där han upplever en potentiell stigning.
• För sin del₃ Den korsar motståndet i den centrala grenen på 6 Ω och 0.15 Ω och på 3 -batteriet.0 V är en potentiell ökning.

På samma sätt används OHM V = i ∙ R -lagen för att fastställa spänningen i varje motstånd, enligt detta:

−20 ∙ i₁ - 6 ∙ i₃ + 3.0 - 0.25 ∙ i₃ −15 ∙ i₁ + 18.0 - 0.5 ∙ i₁ = 0

Beställer villkoren:

(−20 −15 - 0.5) ∙ i₁ - (6 + 0.25) ∙ i₃  = - 3.0 - 18.0

−35.5 ∙ i₁ - 6.25 ∙ i₃ = - 21.0

2) 5 ∙ i₁ + 6.25 ∙ i₃ = 21.0

Andra nät

Den tredje ekvationen erhålls genom att turnera i nätet till höger, börja i noden på kretsen. Det observeras att:

• Yo₂ Gå igenom motståndet på 8 Ω, 0.5 Ω och 0.75 Ω, plus 12 V och 24 V -batterier. Enligt batteriets polaritet är det en ökning av potentialen i 12 V och minskningen i 24 V och minskningen i 24 V.
• Viktig: Turnén i det andra nätet (i ett schema) är emot i₃, Därför spänningarna i motståndet på 6 Ω och 0.25 Ω är potentiella stigningar och har ett positivt tecken. Enligt batteriets polaritet är det en ökning i 12 V och faller i de på 24 V och 3 V.

Med allt detta når du:

−8 ∙ i₂ - 0.5 ∙ i₂ - 0.75 ∙ i₂ + 12.0 - 24.0 + 0.25 ∙ i₃ - 3.0 + 6 ∙ i₃ = 0

3) −25 ∙ i₂ + 6.25 ∙ i₃ = 15.0

Aktuell beräkning

Ekvationer 1), 2) och 3) bildar ett system med 3 linjära ekvationer med 3 okända, vars lösning är:

Yo₁ = 0.381 a; Yo₂ = -0.814 a; Yo₃ = 1.195 a

Det negativa tecknet i nuvarande i₂ betyder att det flyter i motsatt riktning av schemat.