Vinkelräta linjeegenskaper, exempel, övningar

En perpendikulär linje Det är en som bildar en vinkel på 90º med avseende på en annan linje, kurva eller yta. Observera att när två linjer är vinkelräta och på samma plan, när de skärs bildar de fyra identiska vinklar, var och en av 90º.

Om en av vinklarna inte är 90º sägs det att linjerna är sneda. Vinkelräta linjer är ofta i design, arkitektur och konstruktion, till exempel rörnätverket för följande bild.

Figur 1. Rak -vinkelrör och många vinkelräta linjer. Hur många 90º -vinklar kan räknas i den här bilden? Källa: Piqsels.

Orienteringen av vinkelräta linjer kan vara olika, till exempel de som visas nedan:

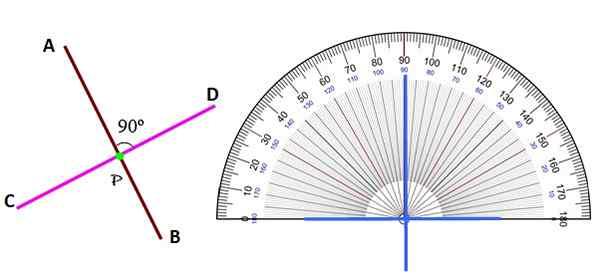
figur 2. Vinkelräta linjer på planet. Källa: f. Zapata.

Oavsett position erkänns de vinkelräta linjerna genom att identifiera vinkeln mellan dem som 90º, med hjälp av transportören.

Observera att till skillnad från de parallella linjerna i planet, som aldrig är korsande, gör den vinkelräta alltid det vid en punkt P, kallad fot av en av linjerna på den andra. Därför är två vinkelräta linjer också Secantes.

Varje linje har oändlig vinkelrätt mot den, eftersom vi bara genom att förskjuta AB -segmentet till vänster eller höger på CD -segmentet, kommer vi att ha en ny vinkelrätt med en annan fot.

Emellertid kallas vinkelrätt som passerar precis genom mittpunkten för ett segment bisektris av nämnda segment.

[TOC]

Exempel på vinkelräta linjer

Vinkelräta linjer är ofta i stadslandskapet. I följande bild (figur 3) bara några av de många vinkelräta linjerna som uppskattas på den enkla fasaden på denna byggnad och dess element som dörrar, kanaler, steg och mer: mer: mer:

Kan tjäna dig: Fourier diskret omvandlad: egenskaper, applikationer, exempel Figur 3. Det finns många vinkelräta linjer på fasaden på en gemensam byggnad som denna. Källa: Richard Kang genom Flickr.

Det goda är att tre linjer vinkelrätt mot varandra hjälper oss att fastställa platsen för punkter och föremål i rymden. Är koordinataxlarna identifierade som X -axel, Axel y och Z -axel, Tydligt synligt i hörnet av ett rektangulärt rum som följande:

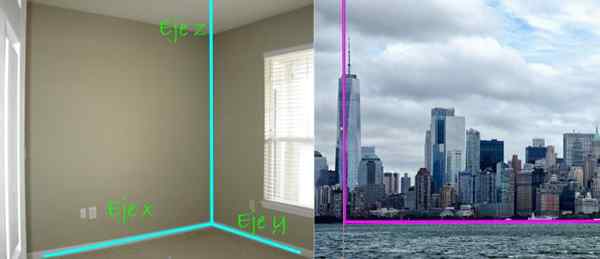Figur 4. Det kartesiska axelsystemet består av tre linjer vinkelrätt mot varandra, var och en har en förmånsriktning i rymden. Vänster bildkrediter: Treybunn 2 genom Flickr. Rätt bild; Nålpix.

I panoramautsikten över staden, till höger, varnar också vinkelrätt mellan skyskrapor och marken. Den första skulle säga att det finns i hela Z -axel, Medan marken är ett plan, som i detta fall är planet Xy.

Om marken utgör planet Xy, Skyskrapan är också vinkelrätt mot alla vägar eller gata, vilket garanterar dess stabilitet, eftersom en lutande struktur är instabil.

Och på gatorna, varhelst rektangulära hörn, finns det vinkelräta linjer. Många vägar och gator har en vinkelrätt layout, förutsatt att marken och geografiska olyckorna tillåter det.

För att plötsligt uttrycka vinkelrätten mellan linjer, segment eller vektorer används symbolen ⊥. Till exempel, om linjen L₁ är vinkelrätt mot linjen L₂, vi skrev:

L₁ ⊥ l₂

Fler exempel på vinkelräta linjer

- I designen är de vinkelräta linjerna mycket närvarande, eftersom många vanliga föremål är baserade på rutor och rektanglar. Dessa quadrilaterals kännetecknas av att ha 90 ° inre vinklar, eftersom deras sidor är två till två parallella:

Det kan tjäna dig: allmän parabola -ekvation (exempel och övningar)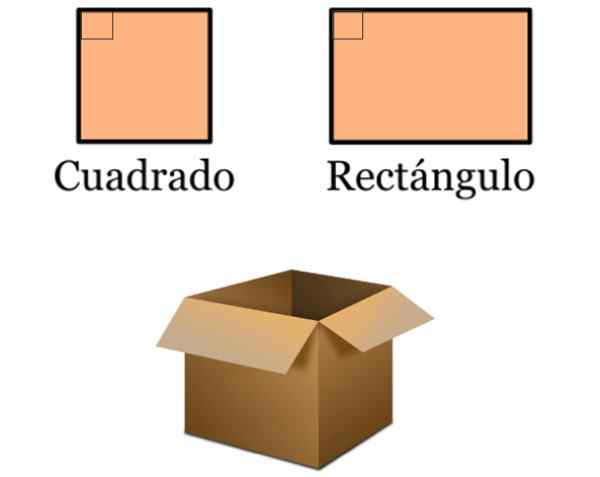 Figur 5. Sorg och rektanglar är en del av många mönster, till exempel den för denna enkla kartong för att lagra varor. Källa: f. Zapata.

- Domstolarna som olika sporter utövas avgränsas av många torg och rektanglar. Dessa innehåller i sin tur vinkelräta linjer.

- Två av segmenten som utgör en rektangel triangel är vinkelrätt mot varandra. Dessa kallas kategorier, Medan den återstående linjen kallas hypotenusa.

- De elektriska fältvektorlinjerna är vinkelräta mot ytan på en elektrostatisk jämvikt.

- För en laddad förare är utrustning och utrustning alltid vinkelrätt mot de för elektriska fält.

- I rörsystem eller kanaler som används för att transportera olika typer av vätskor, till exempel gas som visas i figur 1, är det vanligt för armbågar i rät vinkel. Därför bildar de vinkelräta linjer, så är fallet med ett pannrum:

Figur 6. Rör i en pannrum. Källa: Wikimedia Commons. Roger McLassus/CC BY-S (http: // Creativecommons.Org/licenser/BY-SA/3.0/)

Övningar

- Övning 1

Rita två vinkelräta linjer efter regel och kompass.

Lösning

Det är väldigt enkelt att göra efter dessa steg:

-Den första raden ritas, kallad AB (svart).

-Ovan (eller under om föredragen) av AB Marks Point P, där vinkelrätt kommer att passera. Om P är precis ovanför (eller under) hälften av AB, sa att vinkelrätt är bisektorn för AB -segmentet.

-Med kompassen centrerad på P dras en cirkel som skär AB i två punkter, kallas till 'och B' (röd).

Kan tjäna dig: vänliga eller vänliga nummer: exempel och hur man hittar dem

-Kompassen i A'p öppnas, den fokuserar på en 'och en cirkel ritas som passerar genom P (grön).

-Upprepa föregående steg, men öppnar nu kompassen längden på B'P -segmentet (grönt). Båda omkretsbågarna skärs vid punkt Q under P och naturligtvis i det senare.

-Punkterna P och Q förenas med regeln och den vinkelräta linjen (blå) är redan redo.

-Slutligen måste alla hjälpkonstruktioner noggrant raderas, vilket bara lämnar vinkelrätt.

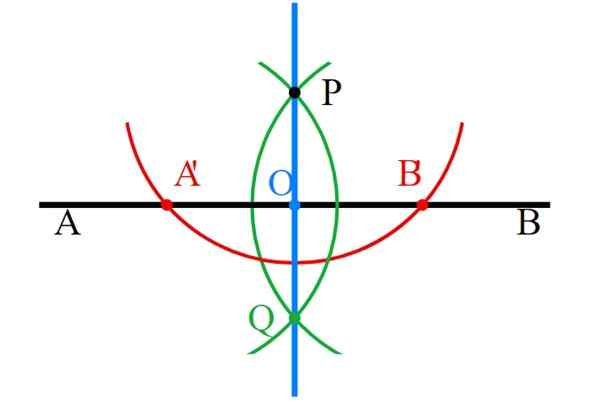Figur 6. Percendular linjer med regel och kompas. Källa: Wikimedia Commons.

- Övning 2

Två rader L₁ och jag₂ De är vinkelräta om deras respektive sluttningar m₁ och M₂ De uppfyller detta förhållande:

m₁ = -1/m₂

Med tanke på linjen y = 5x - 2, hitta en linje vinkelrätt mot den och passera genom punkten (-1, 3).

Lösning

-Först och främst är lutningen för den vinkelräta linjen M_⊥, Som anges i uttalandet. Lutningen för den ursprungliga linjen är M = 5, koefficienten som följer "X". Så:

m_⊥= -1/5

-Sedan byggs ekvationen för den vinkelräta linjen och_⊥, ersätta det tidigare hittade värdet:

och_⊥= -1/5x + b

-Därefter bestäms värdet på B, med hjälp av den punkt som ges av uttalandet, (-1,3), eftersom den vinkelräta linjen måste passera genom den:

y = 3

x = -1

Byter ut:

3 = -1/5 (-1) + B

Värdet på B rensas:

B = 3- (1/5) = 14/5

-Slutligen är den slutliga ekvationen byggd:

och_⊥= -1/5x + 14/5

Referenser

1. Baldor, a. 2004. Platt och rymdgeometri. Kulturpublikationer.
2. Clemens, s. 2001. Geometri med applikationer och problemlösning. Addison Wesley.
3. Matematik är kul. Vinkelrät. Återhämtat sig från: Mathisfun.com.
4. Monterey Institute. Vinkelrät. Återhämtat sig från: MontereyInstitute.org.
5. Wikipedia. Vinkelrät. Återhämtad från: är.Wikipedia.org.