Diskret matematik

Vad är diskret matematik?

De diskret matematik motsvarar ett matematikområde som ansvarar för att studera uppsättningen av naturliga siffror; det vill säga uppsättningen av ändliga och oändliga redovisningsnummer där elementen kan räknas separat, en efter en.

Dessa uppsättningar är kända som diskreta uppsättningar; Ett exempel på dessa uppsättningar är hela nummer, grafer eller logiska uttryck och tillämpas inom olika vetenskapsområden, främst inom datavetenskap eller dator.

Beskrivning

I diskret matematik är processerna numrable, de är baserade på hela siffrorna. Detta innebär att decimalantal inte används och därför används inte heller tillvägagångssättet eller gränserna i andra områden. Till exempel kan en okänd vara lika med 5 eller 6, men aldrig 4,99 eller 5,9.

Å andra sidan, i den grafiska representationen kommer variablerna att vara diskreta och ges från en ändlig uppsättning punkter, som räknas en efter en, som observerats i bilden:

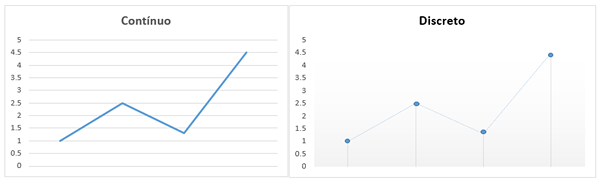
Diskret matematik är född på grund av behovet av att få en exakt studie som kan kombineras och bevisas för att tillämpa den i olika områden.

Vad är diskret matematik för?

Diskret matematik används på flera områden. Bland de viktigaste är följande:

Kombinatorisk

Studera ändliga uppsättningar där elementen kan beställas eller kombineras och återkallas.

Diskret distributionsteori

Studiehändelser som förekommer i utrymmen där prover kan redovisas, där kontinuerliga distributioner används för att närma sig diskreta distributioner, eller motsätta sig.

Informationsteori

Den hänvisar till kodning av information, som används för design och överföring och lagring av data, till exempel liknande signaler.

Kan tjäna dig: Trachtenberg Method: Vad är det, exempel

Datoranvändning

Genom diskret matematik löses problem med algoritmer, liksom vad som kan beräknas och den tid det tar att göra det (komplexitet).

Betydelsen av diskret matematik på detta område har ökat under de senaste decennierna, särskilt för utvecklingen av programmering och Mjukvaror.

Kryptografi

Det är baserat på diskret matematik för att skapa säkerhetsstrukturer eller krypteringsmetoder. Ett exempel på denna applikation är lösenord som skickar separata bitar som innehåller information.

Genom studien kan egenskaperna hos hela siffror och primtal (teori om siffror) skapas eller förstöras.

Logik

Diskreta strukturer används, som vanligtvis bildar en ändlig uppsättning för att demonstrera teorem eller till exempel verifiera programvara.

Grafteori

Det tillåter upplösning av logiska problem, med hjälp av noder och linjer som bildar en typ av graf, som visas i följande bild:

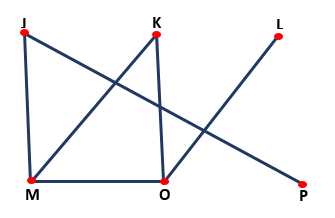Algebra

Det är ett område som är nära kopplat till diskret matematik eftersom algebraiska uttryck är diskreta. Genom dessa elektroniska kretsar utvecklas processorer, programmering (boolean algebra) och databaser (relationella algebra) (relationella algebra).

Geometri

Studera de kombinatoriska egenskaperna hos geometriska objekt, såsom planbeläggning. Å andra sidan gör beräkningsgeometri det möjligt att utveckla geometriska problem genom att tillämpa algoritmer.

Inställningsteori

I diskret matematik är uppsättningarna (ändlig och oändlig dom) det huvudsakliga målet målet. Uppsättningsteorin publicerades av George Cantor, som visade att alla oändliga uppsättningar har samma storlek.

En uppsättning är en grupp element (siffror, saker, djur och människor, bland andra) som är väl definierade; Det vill säga det finns en relation enligt vilken varje element tillhör en uppsättning och uttrycks till exempel en ∈ A.

Kan tjäna dig: Egenskaper för jämlikhet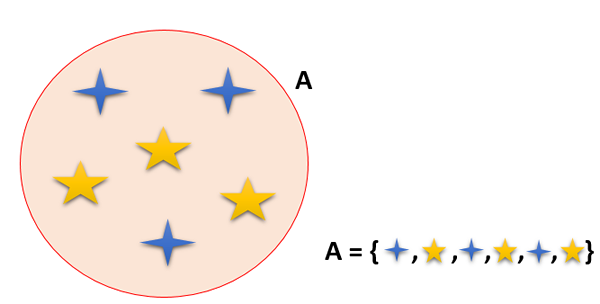

I matematik finns det olika uppsättningar som grupperar vissa siffror enligt deras egenskaper. Således har de till exempel:

- Uppsättning naturliga nummer n = 0, 1, 2, 3, 4, 5, 6, ... +∞.

- Uppsättning av hela siffror e = -∞ ..., -3, -2, -1, 0, 1, 2, 3, ... +∞.

- Delmängd av rationella nummer Q* = -∞ ..., - ¼, - ½, 0, ¼, ½, ... ∞.

- Uppsättning av verkliga siffror r = -∞ ..., -½, -1, 0, ½, 1, ... ∞.

Uppsättningarna namnges med alfabetet bokstäver, i stora bokstäver; Medan elementen namnges i små bokstäver, inuti nycklar () och separeras av komma (,). De är vanligtvis representerade på diagram som Venn och Caroll, såväl som beräkningsmässigt.

Med grundläggande operationer som union, korsning, komplement, skillnad och kartesisk produkt, hanteras uppsättningarna och deras element, baserat på tillhörande relation.

Det finns flera typer av uppsättningar, de mest studerade i diskret matematik är följande:

Ändlig uppsättning

Det är en som har ett ändligt antal element och som motsvarar ett naturligt antal. Således är till exempel A = 1, 2, 3.4 en ändlig uppsättning som har 4 element.

Oändlig redovisningsuppsättning

Det är en där det finns en korrespondens mellan elementen i en uppsättning och de naturliga siffrorna; det vill säga från ett element kan alla element i en uppsättning listas successivt.

På detta sätt kommer varje element att motsvara varje element i uppsättningen naturliga siffror. Till exempel:

Hela hela siffrorna z = ... -2, -1, 0, 1, 2 ... kan listas som z = 0, 1, -1, 2, -2 .... På detta sätt är det möjligt att göra en en -till -en korrespondens mellan elementen i Z och de naturliga siffrorna, vilket kan ses i följande bild:

Kan tjäna dig: Beräkning av tillvägagångssätt med skillnader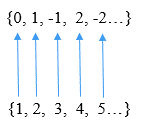

Diskretisering

Det är en metod som används för att lösa kontinuerliga problem (modeller och ekvationer) som måste omvandlas till diskreta problem, där lösningen är känd med tillvägagångssättet för lösningen av det kontinuerliga problemet.

Sett på annat sätt försöker diskretiseringen få en begränsad mängd av en oändlig uppsättning punkter; På detta sätt förvandlas en kontinuerlig enhet till enskilda enheter.

Generellt används denna metod i den numeriska analysen, till exempel i lösningen av en differentiell ekvation, genom en funktion som representeras av en begränsad mängd data i dess domän, även när detta är kontinuerligt.

Ett annat exempel på diskretiseringen är dess användning för att konvertera en analog med digital signal, när kontinuerliga signalenheter omvandlas till enskilda enheter (de är diskretiserade) och sedan kodas och kvantifieras för att erhålla digital signal.

Referenser

1. Grimaldi, r. P. (1997). Diskret och kombinatorisk matematik. Redaktör Addison Wesley Iberoamericana.
2. Ferrando, v. Gregori. (nittonhundranittiofem). Diskret matematik. Reverte.
3. Jech, T. (2011). Inställningsteori. Stanford Encyclopedia of Philosophy.
4. José Francisco Villalpando Becerra, en. G. (2014). Diskret matematik: Tillämpningar och övningar. Patria Redaktionsgrupp.
5. Landau, r. (2005). Dator, till första kursen i vetenskapligt.
6. Merayo, f. G. (2005). Diskret matematik. Thomson -redaktion.
7. Rosen, K. H. (2003). Diskret matematik och dess tillämpningar. McGraw-Hill-redaktion.
8. Schneider, D. G. (nittonhundranittiofem). En logisk metod för diskret matematik.