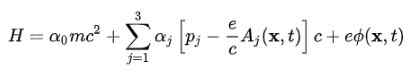Aomisk modell av Dirac Jordan -egenskaper och postulates

han Dirac-Jordan Atomic Model Det är den relativistiska generaliseringen av den Hamiltoniska operatören i ekvationen som beskriver kvantvågfunktionen. Till skillnad från den föregående modellen, Schrodingers, är det inte nödvändigt att införa snurret genom Paulis uteslutningsprincip, eftersom det verkar naturligt.

Dessutom innehåller Dirac-Jordan-modellen relativistiska korrigeringar, spinorgan-interaktion och Darwins term, som står för den fina strukturen i atomens elektroniska nivåer.

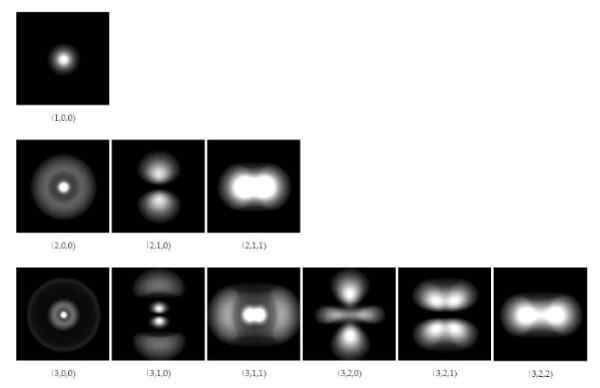
Figur 1. Elektroniska orbitaler i väteatomen för de första tre energinivåerna. Källa: Wikimedia Commons.

Från och med 1928. M. Dirac (1902-1984) och Pascual Jordan (1902-1980) föreslogs för att generalisera kvantmekaniken som utvecklats av Schrodinger, för att inkludera korrigeringarna i Einsteins specialrelativitet.

Dirac -del av Schrodinger -ekvationen, som består av en differentiell operatör, kallad Hamiltonian, som fungerar på en funktion som kallas Elektronvågfunktionen. Schrodinger tog emellertid inte hänsyn till de relativistiska effekterna.

Vågfunktionslösningar gör det möjligt att beräkna de regioner där elektronen runt kärnan hittas med en viss sannolikhet. Dessa regioner eller områden kallas Orbitaler Och de är beroende av vissa diskreta kvantantal, som definierar elektronens energi och vinkelmoment. 

[TOC]

Postulat

I kvantmekaniska teorier, oavsett om det är relativistiskt eller inte, finns det inget begrepp om banor, eftersom varken positionen eller hastigheten på elektronen kan specificeras samtidigt. Och dessutom leder det att specificera en av variablerna till total imprecision i den andra.

Hamiltonian är för sin del en matematisk operatör som verkar på kvantvågfunktionen och är byggd av elektronenergi. Till exempel har en gratis elektron total energi och det beror på dess linjära momentum p Således:

E = (p²)/ 2m

För att bygga Hamiltonian börjar det från detta uttryck och ersätts p Av kvantoperatören för fart: 

p = -I ħ ∂ /∂r 

Det är viktigt att notera att villkoren p och p De är olika, eftersom den första är fart och den andra är Differentiell operatör associerad med fart. 

Kan tjäna dig: atommodell av leukipo: postulates, begränsningar, betydelse

Dessutom är jag den imaginära enheten och ħ Planck -konstanten dividerad med 2π, på detta sätt erhålls Hamiltonian -operatören H av den fria elektronen:

H = (ħ²/2m) ∂² /∂r² 

För att hitta elektronens hamiltonian i atomen läggs elektroninteraktionen med kärnan: 

H = (ħ2/2m) ∂² /∂r²  - Eφ (R)

I det föregående uttrycket är den elektroniska elektriska laddningen och φ (r) den elektrostatiska potentialen som produceras av den centrala kärnan.

Nu agerar operatör H på vågfunktionen ψ enligt Schrodinger -ekvationen, som är skriven så här:

H ψ = (i ħ ∂ /∂t) ψ

De fyra postulaten av Dirac

Första postulatet: Den relativistiska vågekvationen har samma struktur som Schrodingers vågekvation, vilka förändringar är H:

H ψ = (i ħ ∂ /∂t) ψ

Andra postulat: Hamiltonian-operatören är byggd baserat på Einsteins energi-momentum-relation, som är skriven så här:

E = (m² c⁴ + p² c²)^1/2

I det tidigare förhållandet, om partikeln har fart P = 0 så har du den berömda ekvationen E = MC² som hänför sig till vilande energi för en massa massa m med ljusets hastighet c.

Tredje postulatet: För att få Hamiltonian -operatören används samma kvantiseringsregel som används i Schrodinger -ekvationen:

p = -I ħ ∂ /∂r

I början var det inte klart hur han skulle hantera denna differentiella operatör som agerade inom en kvadratrot, så Dirac försökte få en linjär Hamiltonisk operatör i momentumoperatören och därifrån uppstod hans fjärde postulat.

Postulat: För att bli av med kvadratroten i den relativistiska energiformeln föreslog Dirac följande struktur för E²:

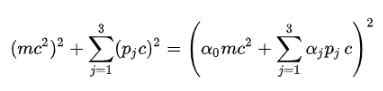
Naturligtvis är det nödvändigt att bestämma alfakoefficienterna (a0, a1, a2, a3) så att detta uppfylls.

Dirac -ekvationen

Dirac -ekvationen höjdes först för den fria elektronen med hjälp av strukturen som föreslogs i det fjärde postulatet. Det återstår på följande sätt: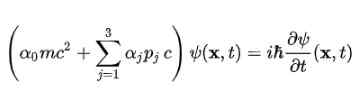

Det kan tjäna dig: Hör Force: Surface and Mass Forces

I sin kompakta form anses Dirac -ekvationen vara en av de vackraste matematiska ekvationerna i världen:

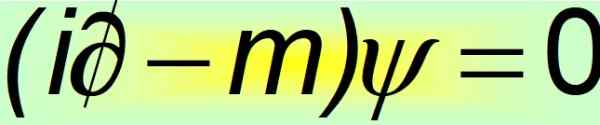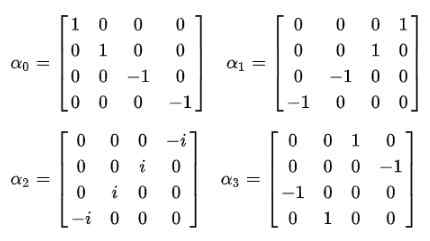
figur 2. Dirac Equation Compact. Källa: f. Zapata.

Och det är när det bevisas att de ständiga Alfas inte kan vara skalära mängder. Det enda sättet på vilket jämlikheten för det fjärde postulatet uppfylls är att de är 4 × 4 konstant matriser, som är kända som Dirac Matrices:

Det observeras omedelbart att vågfunktionen upphör att vara en skalfunktion och blir en fyrkomponentvektor Esmanör:

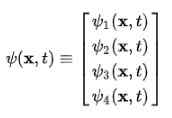
Dirac-Jordan's Atom

För att erhålla atommodellen är det nödvändigt att flytta från den fria elektronekvationen till den för elektronen i det elektromagnetiska fältet som produceras av atomkärnan. Denna interaktion beaktas genom att integrera den potentiella skalaren φ och den potentiella vektorn TILL I Hamiltonian:

Vågfunktionen (espinor) som är resultatet av att integrera denna Hamiltonian har följande egenskaper: 

- Det uppfyller den speciella relativiteten, eftersom den tar hänsyn till elektronens inre energi (första terminen i den relativistiska Hamiltonian)

- Den har fyra lösningar som motsvarar de fyra komponenterna i espinor

- De två första lösningarna motsvarar en för att snurra +½ och den andra till snurret - ½ 

- Slutligen förutspår de andra två lösningarna förekomsten av antimateria, eftersom de motsvarar den av motsatsernas positroner.

Den stora fördelen med Dirac -ekvationen är att de grundläggande Hamiltonian -korrigeringarna av Schrodinger H (O) kan delas upp i flera termer som vi kommer att visa nedan:

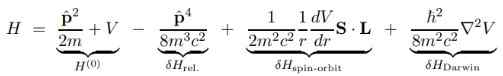
I det föregående uttrycket V är den potentiella skalaren, eftersom den potentiella vektorn TILL Det är ogiltigt om det är tänkt för den centralstationära protonen och det är därför det inte visas.

Anledningen till att DIRAC: s korrigeringar avseende Schrodinger -lösningar i vågfunktionen är subtila. De uppstår av det faktum att de tre sista termerna för den korrigerade Hamiltonian alla är uppdelade med hastigheten C på torget, ett enormt nummer, vilket gör dessa termer numeriskt små.

Det kan tjäna dig: Vy Canis Majoris: Discovery, Egenskaper, struktur, träning och utveckling

Relativistiska korrigeringar till energispektrumet

Med hjälp av Dic-Jordan-ekvationen finns korrigeringar till elektronenergispektrumet i väteatomen. Det finns också korrigeringar för energi i atomer med mer än en elektron ungefär genom en metod som kallas teorin om störningar.

På liknande sätt låter Dirac -modellen dig hitta korrigering av fin struktur vid väteenerginivåer. 

Ännu mer subtila korrigeringar som hyperfinstrukturen och lammskiftet erhålls emellertid från mer avancerade modeller som Campos kvantteori, Född just på grund av Dirac -modellens bidrag.

Följande figur visar hur DIRAC: s relativistiska korrigeringar är på energinivåer:

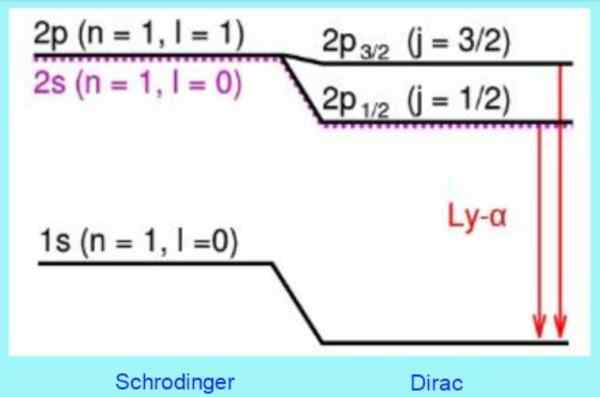Figur 3. Dirac -modellkorrigeringar vid väteatomnivåer. Källa: Wikimedia Commons.

Till exempel förutsäger lösningarna på DIRAC -ekvationen korrekt en förskjutning som observerats på nivå 2s. Det är den välkända fina strukturkorrigeringen i Lyman -linjen - Alfa för vätespektrumet (se figur 3).

Förresten, den fina strukturen är namnet som får i atomfysiken utspelningen av linjerna i utsläppsspektrumet för atomerna, vilket är en direkt följd av den elektroniska snurret.

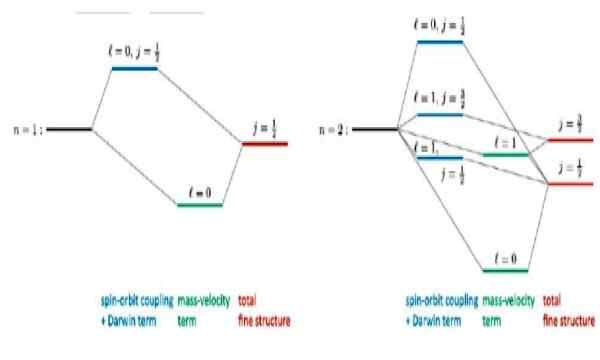Figur 4. Fin struktur som utvecklas för bastillstånd n = 1 och det första upphetsade tillståndet n = 2 i väteatomen. Källa: r wirnata. Relativistiska korrigeringar till väteliknande atomer. Forskning.netto

Intresseartiklar

Bros.

Chadwick atommodell.

Heisenberg atommodell.

Perrin atommodell.

Thomson Atomic Model.

Dalton Atomic Model.

Schrödinger Atomic Model.

Demokritusatommodell.

Leucipo Atomic Model.

Bohr atommodell.

Nuvarande atommodell.

Referenser

1. Atomteori. Återhämtat sig från Wikipedia.org.
2. Elektronmagnetiskt ögonblick. Återhämtat sig från Wikipedia.org.
3. Quanta: En handbok med koncept. (1974). Oxford University Press. Återhämtat sig från Wikipedia.org.
4. Dirac Jordan Atomic Model. Återhämtat sig från Prezi.com.
5. Det nya kvantuniverset. Cambridge University Press. Återhämtat sig från Wikipedia.org.