Pendulrörelse

Vad är pendular rörelse?

han pendulrörelse Det är en svängande rörelse gjord av ett mer eller mindre tungt föremål, kallad en pendel, upphängd av ett lätt rep eller stång, fixerad i dess andra ände.

Pendeln tilldelas en initial impuls och får svänga, på detta sätt beskriver objektet rundturbågar. Detta är principen om drift av pendelklockor, gungor, gungstolar och Metronom av pendel, som används för att markera tiderna i musik.

Pendel svänger, visar hastighet och acceleration (Wikipedia.org)

Det sägs att år 1581 observerade Galileo Galilei svängningen av en lampa i Pisas katedral, och observerade att även om amplituden för ljusstaken svängde minskade på grund av friktion med luften, inte varaktigheten av varaktighetens varaktighet varaktighet av cykelns varaktighet.

Detta fick uppmärksamheten från Galileo, som beslutade att fortsätta med studien och bestämde att pendelperioden inte beror på degen, utan på kvadratroten av repets längd, vilket kommer att ses senare.

Egenskaper hos pendulören

En pendel är väldigt lätt att bygga, eftersom det räcker med en lod som hänger av en bomullstråd och håller i andra änden med fingrarna eller genom att binda den till ett stöd som en spik.

Efter den lilla initiala impulsen är vikten ansvarig för att hålla pendeln oscillerande, även om friktionen minskar rörelsens amplitud tills den äntligen upphör.

Det huvudsakliga inslaget i pendulörelsen är att vara repetitiv, eftersom det är en rörelse av sväng. För att underlätta din studie är det bekvämt att göra några förenklingar att fokusera på en enklare modell, kallad enkel pendel.

Den enkla pendeln

Barnet i gungan kan modelleras som en enkel pendel

Det är ett idealiskt system som består av en lod, betraktas som en punktlig massa m, med förbehåll för ett lätt och oextlöst rep av längd L. Egenskaperna för detta system är:

• Har en repetitiv och periodisk rörelse, bestående av att gå fram och tillbaka en båge av radieomkrets lika med L.
• Tar inte hänsyn till friktion.
• Rörelsens amplitud är liten (< 5º).
• Perioden är oberoende av massa m, Och det beror enbart på längd L av pendeln.

Kan tjäna dig: resulterande vektor: beräkning, exempel, övningar

Formler och ekvationer

Följande är ett enkelt pendeldiagram, på vilket två krafter agerar: vikten P av storlek mg, som riktas vertikalt ner och spänningen T På repet. De betraktas inte som friktion.

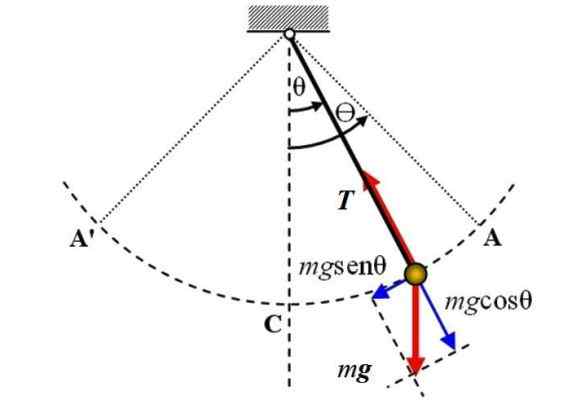Gratis kroppsdiagram över det enkla pendeln. Källa: Wikimedia Commons.

Referensaxeln är den vertikala axeln och sammanfaller med positionen θ = 0, därifrån mäts vinkelförskjutningen θ, antingen i en eller annan riktning. Skylten + kan tilldelas höger i figuren.

För att studera pendelrörelsen väljs ett koordinatsystem med ursprunget i själva pendeln. Detta system har en tangentiell koordinat till A'CA -omkretsbågen som beskrivs av pendeln, såväl som en radiell koordinat, riktad mot banans centrum.

Just nu som visas i figur_t, ansvarar för att få den tillbaka. Det varnas för figuren att denna komponent är en känsla i strid med rörelsen.

När det gäller spänningen på repet är den balanserad med komponenten i vikten mgcosθ.

Nettokraften är då, den som kallas f_t Och enligt Newtons andra lag är det lika med produkten Mass × Acceleration, Och detta är i sin tur det andra härrörande från linjär förskjutning s, Vad är bågen som reste av pendeln. Så:

Vinkelförskjutning 

Ekvationen måste uttryckas i termer av en enda variabel och komma ihåg att vinkelförskjutning θ och bågen reste är relaterade av ekvation:

Det kan tjäna dig: andra lagen om termodynamik: formler, ekvationer, exempel

s = l.θ

Massan avbryts på båda sidor och om amplituden är liten, är vinkeln också, på ett sätt som följer följande tillvägagångssätt:

synd θ ≈ θ

Med detta erhålls följande differentiella ekvation för variabel θ (t):

Denna ekvation är mycket lätt att lösa, eftersom dess lösning är en funktion vars andra derivat är själva funktionen. Det finns tre alternativ: ett kosinus, ett bröst eller ett exponentiellt. Kosinusfunktionen väljs för vinkelförskjutning θ (t), eftersom det är en välkänd och enkel att hantera funktion.

Läsaren kan kontrollera, härleda två gånger, att följande funktion uppfyller differentiell ekvation:

θ (t) = θ_m cos (ωt + φ)

Där θ_m Det är maximal vinkel som pendeln rör sig med avseende på vertikal och vinkelfrekvens ω är:

Konstanten φ läggs till för att ge generaliteten till lösningen och passar i enlighet med de initiala förhållandena.

Periodekvation

Rörelsens t är den tid det tar att utföra en cykel och definieras som:

Ersätter ω:

Som tidigare fastställts beror perioden inte på pendelmassan, utan bara på dess längd.

Exempel på pendulär rörelse

Hjärtfrekvens

Galileo hade förekomsten av att mäta hjärtfrekvensen för människor och justera pendelens längd fram till perioden med pulseringarna i hjärtat av en person sammanfaller.

Pendelklockan

Detta är utan tvekan ett av de mest bekanta pendulära rörelsexemplen. Tillverkningen av pendelklockor har både vetenskap och konst. Den holländska fysikern Christian Huygens (1629-1695) utvecklade den första pendelklockan 1656, baserad på studien för år sedan av Galileo.

Kan tjäna dig: böljande optik

Foucaults pendel

Foucault pendel. Källa: Wikimedia Commons.

Det är en något annorlunda pendel än beskrivet ovan, eftersom det kan vända i något vertikalt plan. Det skapades av den franska fysikern Léon Foucault (1819-1868) och används för att visualisera jordens rotation.

Träning löst

En enkel pendel passerar varje 0.5 s för jämviktspositionen. Vad är trådens längd?

Lösning

Eftersom perioden är den tid det tar att göra en komplett cykel, där den passerar två gånger genom jämviktspositionen: en först och den andra tillbaka, sedan:

T = 2 × 0.5 s = 1 s

Av:

Trådens längd l rensas:

Tråden mäter 0.25 m eller 25 cm lång.

Referenser

1. Figueroa, D. (2005). Serie: Physics for Science and Engineering. Volym 2. Dynamisk. Redigerad av Douglas Figueroa (USB).
2. Giambattista, a. 2010. Fysik. 2: a. Ed. McGraw Hill.
3. Giancoli, D.  2006. Fysik: Principer med applikationer. Sjätte. Ed Prentice Hall.
4. Katz, D. 2013. Fysik för forskare och ingenjörer. Stiftelser och anslutningar. Cengage Learning.
5. Riddare, r.  2017. Fysik för forskare och teknik: En strategistrategi.  Pearson.