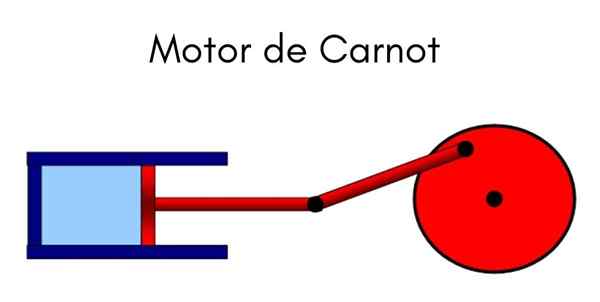
Carnot -maskin

Vad är Carnot -maskinen?

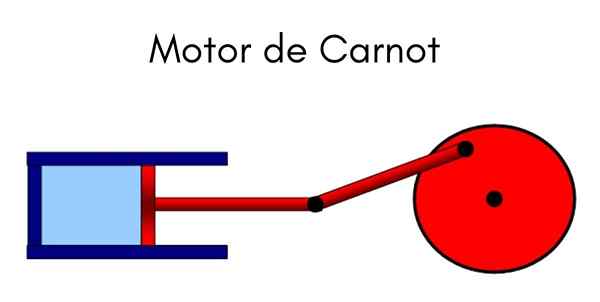
De Carnot -maskin Det är en idealisk cyklisk modell där värme används för att göra ett jobb. Systemet kan förstås som en kolv som rör sig inuti en cylinder som komprimerar en gas. Cykeln som utövas är den av Carnot, uttalad av fadern till termodynamik, den franska fysikern och ingenjören Nicolas Leonard Sadi Carnot.

Carnot uppgav denna cykel i början av 1800 -talet. Maskinen utsätts för fyra tillståndsvariationer, växlande förhållanden som konstant temperatur och tryck, där en variation av volymen bevisas vid komprimering och utvidgning av gas.

Formler

Enligt Carnot, som utsätter den perfekta maskinen för temperatur- och tryckvariationer är det möjligt att maximera den erhållna prestandan.

Carnot -cykeln måste analyseras separat i var och en av dess fyra faser: isotermisk expansion, adiabatisk expansion, isotermisk komprimering och adiabatisk komprimering.

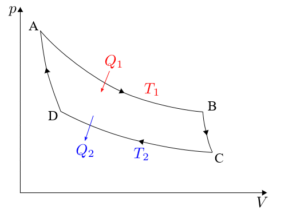
Formlerna som är associerade med var och en av faserna i den cykel som utövas på Carnot -maskinen kommer att beskrivas nedan.

Isotermisk expansion (A → B)

Lokalerna i denna fas är följande:

• Gasvolym: Det går från minsta volym till en genomsnittlig volym.
• Mätningstemperatur: konstant temperatur T1, högt värde (T1> T2).
• Maskintryck: Gå ner från P1 till P2.

Den isotermiska processen innebär att temperaturen T1 inte varierar under denna fas. Värmeöverföring inducerar gasutvidgning, vilket inducerar rörelse på kolven och producerar mekaniskt arbete.

När gasen expanderar presenterar gasen en viss tendens att svalna. Den absorberar emellertid värmen som släpps ut av temperaturkällan och under dess utvidgning upprätthåller den konstant temperatur.

Kan tjäna dig: vad är den linjära hastigheten? (Med lösta övningar)

Eftersom temperaturen förblir konstant under denna process förändras inte den inre energin i gasen, och all värme som absorberas av gasen förvandlas effektivt till arbete till arbete. Så:

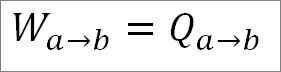
Å andra sidan, i slutet av denna fas av cykeln är det också möjligt att erhålla tryckvärdet med den ideala gasekvationen för den. På detta sätt har du följande:

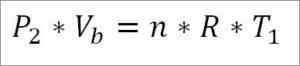
I detta uttryck:

• P₂: Tryck i slutet av fasen.
• V_b: Volym vid punkt B.
• N: Antal mol gas.
• S: Universal konstant av idealiska gaser. R = 0,082 (atm*liter)/(mol*k).
• T1: Absolut initial temperatur, Kelvin grader.

Adiabatisk expansion (B → C)

Under denna fas av processen utförs gasutvidgning utan att behöva byta värme. På detta sätt beskrivs lokalerna nedan:

• Gasvolym: Det går från den genomsnittliga volymen till en maximal volym.
• Mätningstemperatur: Gå ner från T1 till T2.
• Maskintryck: konstant P2 -tryck.

Den adiabatiska processen innebär att P2 -trycket inte varierar under denna fas. Temperaturen minskar och gasen fortsätter att expandera tills den når maximalt för sin volym; det vill säga kolven når toppen.

I detta fall kommer det utförda arbetet från gasens inre energi och dess värde är negativt eftersom energi minskar under denna process.

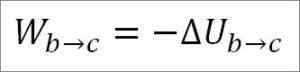
Förutsatt att det är en idealisk gas, hävdas teorin att gasmolekyler endast har kinetisk energi. Enligt termodynamikprinciperna kan detta härledas av följande formel:

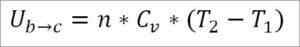
I denna formel:

• ∆u_{B → C}: Intern energivariation av den ideala gasen mellan punkterna B och C.
• N: Antal mol gas.
• CV: Gasmolar värmekapacitet.
• T1: Absolut initial temperatur, Kelvin grader.
• T2: Absolut sluttemperatur, Kelvin Degrees.

Kan tjäna dig: isobarisk process: formler, ekvationer, experiment, övningar

Isotermisk komprimering (C → D)

I denna fas börjar gaskomprimeringen; det vill säga kolven mobiliseras i cylindern, med vilken gasen kontrakterar sin volym.

Villkoren i denna process beskrivs nedan:

• Gasvolym: Det går från den maximala volymen till en mellanvolym.
• Mätningstemperatur: konstant temperatur T2, reducerat värde (T2 < T1).
• Maskintryck: Öka från P2 till P1.

Här ökar trycket på gasen, så det börjar komprimera. Temperaturen förblir emellertid konstant och därför är den inre energivariationen på gasen noll.

Analog till den isotermiska expansionen är arbetet lika med systemets värme. Så:

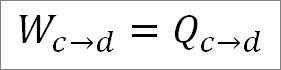
Det är också möjligt att hitta trycket vid denna tidpunkt med den ideala gasekvationen.

Adiabatisk komprimering (D → A)

Detta är den sista fasen av processen, där systemet återgår till dess ursprungliga förhållanden. För att göra detta beaktas följande villkor:

• Gasvolym: Det går från en mellanvolym till en minsta volym.
• Mätningstemperatur: Öka från T2 till T1.
• Maskintryck: konstant tryck P1.

Värmekällan som ingår i systemet i föregående fas tas bort, så att den perfekta gasen kommer att höja sin temperatur under tiden trycket förblir konstant.

Gasen återgår till de initiala temperaturförhållandena (T1) och vid sin volym (minimum). Återigen kommer det utförda arbetet från gasens inre energi, så du måste:

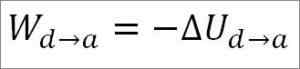
I likhet med fallet med adiabatisk expansion är det möjligt att erhålla variationen av gasenergi genom följande matematiska uttryck:

Kan tjäna dig: kalciumfluorid (CAF2): struktur, egenskaper, användningar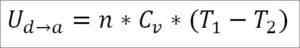

Hur fungerar Carnot -maskinen?

Carnot -maskinen fungerar som en motor där prestanda maximeras genom variation av isotermiska och adiabatiska processer, och växlar faserna av expansion och förståelse av en idealisk gas.

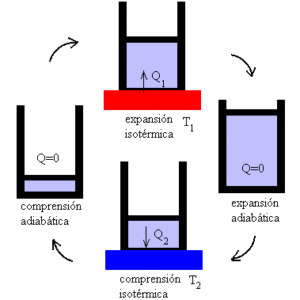
Mekanismen kan förstås som en idealisk anordning som utövar ett jobb som utsätts för värmevariationer, med tanke på förekomsten av två temperaturflöden.

I det första fokuset utsätts systemet för en T1 -temperatur. Det är en hög temperatur som utsätter systemet att stressa och producerar gasutvidgning.

I sin tur översätts detta till genomförandet av ett mekaniskt verk som möjliggör mobilisering av kolven ur cylindern, och vars gräns endast är möjlig genom adiabatisk expansion.

Sedan kommer det andra fokuset, där systemet utsätts för en T2 -temperatur, mindre än T1; det vill säga mekanismen är föremål för kylning.

Detta inducerar värmeekstraktion och gaskrossning, som når sin initiala volym efter adiabatisk komprimering.

Ansökningar

Carnot -maskinen har använts allmänt tack vare sitt bidrag i förståelsen av de viktigaste aspekterna av termodynamik.

Denna modell låter dig tydligt förstå variationerna av ideala gaser som är föremål för temperatur- och tryckförändringar, vilket är en referensmetod när du utformar riktiga motorer.