Kompletterande vinklar som och hur beräknas, exempel, övningar

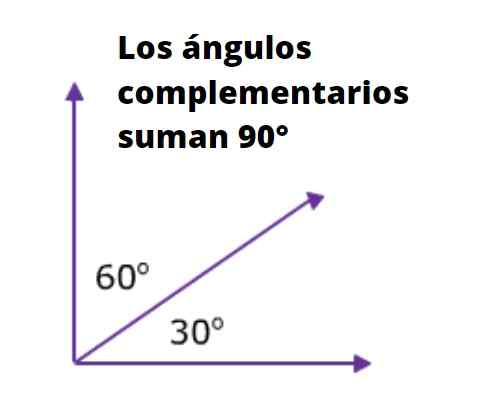
Två eller flera vinklar är kompletterande vinklar Om summan av dess åtgärder motsvarar den för en rätt vinkel. Som känt är måttet på en rätt vinkel i grader 90º, och i radianer är det π/2.

Till exempel är de två vinklarna intill hypotenusen av en rektangel triangel komplement till varandra, eftersom summan av deras åtgärder är 90º. Följande figur är mycket illustrativ om det:

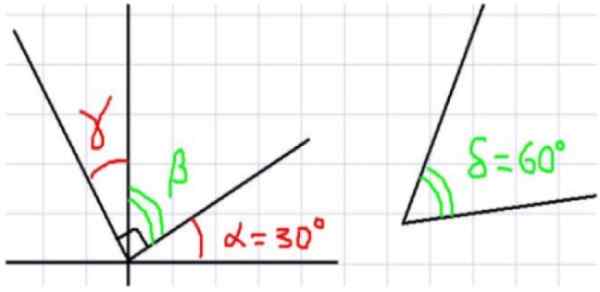Figur 1. Till vänster, flera vinklar med ett gemensamt toppunkt. Till höger en vinkel på 60º som kompletterar vinkeln a (alfa). Källa: f. Zapata.

Figur 1 visar totalt fyra vinklar. α och ß är komplementära eftersom de är intilliggande och dess fulla summa en rätt vinkel. På liknande sätt är ß komplement till y, där det följer att y och a är av lika mått.

Nu, eftersom summan av a och 5 är lika med 90 grader, kan det sägas att a och Δ är komplementära. Eftersom ß och 5 har samma komplementära a, kan det dessutom sägas att ß och 5 har samma mått.

 [TOC]

Exempel på kompletterande vinklar

I följande exempel uppmanas att hitta de okända vinklarna, indikerade med förhör i figur 2.

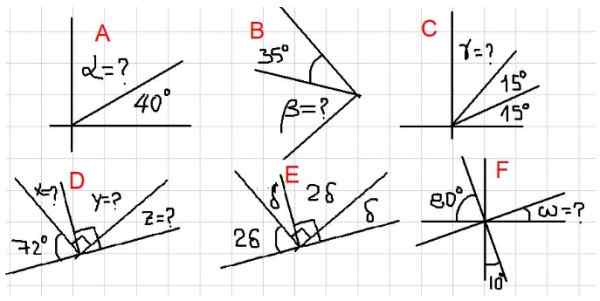figur 2. Olika exempel på kompletterande vinklar. Källa: f. Zapata.

- Exempel A, B och C

Följande exempel är i ordning av komplexitet.

Exempel a

I den övre figuren har vi att de angränsande vinklarna α och 40º lägger till en rätt vinkel. Det är a + 40º = 90º, därför a = 90º- 40º = 50º.

Exempel B

Eftersom ß är komplementärt med vinkeln 35º, sedan β = 90º - 35º = 55º.

Kan tjäna dig: ortoedro: formler, område, volym, diagonal, exempel

Exempel c

Från figur 2c, summan av y + 15º + 15º = 90º. Det vill säga att y är komplement till vinkel 30 = 15º + 15º. Så att:

y = 90º- 30º = 60º

- Exempel D, E och F

I dessa exempel är det fler vinklar involverade. För att hitta de okända måste läsaren tillämpa begreppet kompletterande vinkel så många gånger som behövs.

Exempel D

Eftersom X är komplement till 72º följer det att x = 90º - 72º = 18º. Dessutom och det är komplementärt med x, sedan y = 90º - 18º = 72º.

Slutligen är Z kompletterande till och. Från alla ovanstående följer det:

Z = 90º - 72º = 18º

Exempel E

Vinklarna Δ och 2Δ är komplementära, därför Δ + 2Δ = 90º.

Det är 3Δ = 90º, vilket innebär att Δ = 90º / 3 = 30º.

Exempel f

Om vi ​​kallar vinkeln mellan ω och den av 10, måste den sedan kompletteras till dem, eftersom det observeras att deras fullständiga summa är en rätt vinkel. Där det följer att u = 80º. Eftersom du är kompletterande med ω, då ω = 10º.

Övningar

Tre övningar föreslås nedan. I dem alla måste värdet på vinklar a och b hittas i grader, så att förhållandena som visas i figur 3 är uppfyllda.

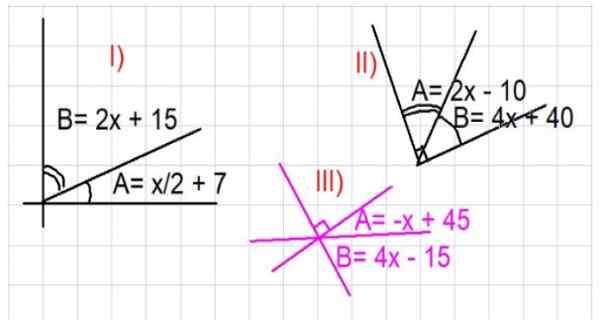Figur 3. Illustrationer för kompletterande vinklarövningar. Källa: f. Zapata.

- Övning 1

Bestäm värdena på vinklar a och b i del I) i figur 3.

Lösning

Från den visade figuren ser man att A och B är komplementära, därför A + B = 90º. Uttrycket av A och B ersätts som en funktion av X som ges i del I):

Kan tjäna dig: konvergensradio: definition, exempel och övningar löst

(x/2 + 7) + (2x + 15) = 90

Då grupperas termerna ordentligt och en enkel linjär ekvation erhålls:

(5x/2) + 22 = 90

Att subtrahera 22 i båda medlemmarna är:

5x/2 = 90 -22 = 68

Och slutligen rensas värdet på X:

x = 2*68/5 = 136/5

Nu hittas vinkeln som ersätter värdet på x:

A = (136/5)/2 +7 = 103/5 = 20,6 º.

Medan vinkel B är:

B = 2*136/5 + 15 = 347/5º = 69.4º .

- Övning 2

Hitta värdena på vinklar A och B för Image II, figur 3.

Lösning

Återigen, eftersom A och B är komplementära vinklar, måste du: A + B = 90º. Att ersätta uttrycket av A och B som en funktion av X som ges i del II) i figur 3 är:

(2x - 10) + (4x +40) = 90

De liknande termerna grupperas för att erhålla ekvationen:

6 x + 30 = 90

Att dela båda medlemmarna mellan 6 erhålls:

x + 5 = 15

Där det följer att x = 10º.

Därför:

A = 2*10 - 10 = 10º

B = 4*10 + 40 = 80º.

- Övning 3

Bestäm värdena på vinklar a och b i del III) i figur 3.

Lösning

Figuren analyseras noggrant för att leta efter kompletterande vinklar. I det här fallet måste du + b = 90 grader. Ersätta uttrycket av A och B som en funktion av X som ges i figuren har du:

(-X +45) + (4x -15) = 90

3 x + 30 = 90

Att dela båda medlemmarna med 3 är följande:

x + 10 = 30

Där det följer att x = 20º.

Det vill säga att vinkeln a = -20 +45 = 25º. Och för sin del: B = 4*20 -15 = 65º.

Vinkelräta sidor

Det sägs att två vinklar är vinkelräta sidor Om varje sida har motsvarande vinkelrätt i den andra. Följande figur klargör konceptet:

Kan tjäna dig: sammansatt succession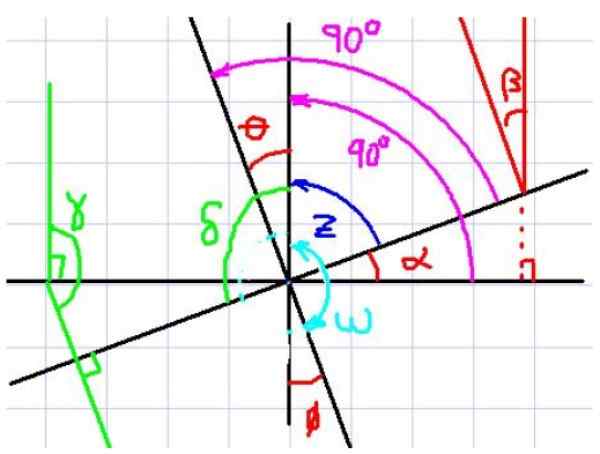Figur 4. Vinkelräta sidor. Källa: f. Zapata.

I figur 4 observeras till exempel vinklarna a och θ. Lägg nu märke till att varje vinkel har motsvarande vinkelrätt i den andra vinkeln.

Man ser också att a och θ har samma komplementära vinkel z, Därför drar observatören omedelbart slutsatsen att α och θ har samma mått. Det verkar då som om två vinklar har vinkelräta sidor med varandra, de är desamma, men låt oss se ett annat fall.

Tänk nu på vinklarna a och ω. Dessa två vinklar har också motsvarande vinkelräta sidor, men det kan inte sägas att de har lika mått, eftersom den ena är akut och den andra är stöt.

Observera att ω + θ = 180º. Förutom θ = α. Om du ersätter detta uttryck av Z i den första ekvationen får du:

5 + α = 180º, eftersom Δ och a är vinklar på ömsesidigt vinkelräta sidor.

Allmän regel för vinkelräta sidor vinklar 

Från ovannämnda kan en regel som alltid uppfylls att vinklarna har vinkelräta sidor kan fastställas:

Om två vinklar är ömsesidigt vinkelräta sidor, är de samma om båda är akuta eller båda är stöt. Annars, om den ena är akut och den andra är stöt, är de kompletterande, det vill säga de lägger till 180º.

Tillämpa denna regel och med hänvisning till vinklarna i figur 4 kan vi bekräfta följande:

α = β = θ = φ

y = Δ

Med ω kompletterande vinkel på a, β, θ och φ.

Referenser

1. Baldor, J. TILL. 1973. Platt och rymdgeometri. Centralamerikansk kultur. 
2. Matematiska lagar och formler. Vinkelmätningssystem. Hämtad från: Ingemecanica.com.
3. Wentworth, g. Planetgeometri. Återhämtat sig från: Gutenberg.org.
4. Wikipedia. Kompletterande vinklar. Återhämtad från: är.Wikipedia.com
5. Wikipedia. Transportband. Återhämtad från: är.Wikipedia.com
6. Zapata f. Goniometer: Historia, delar, operation. Hämtad från: Lifer.com