Central symmetriegenskaper, exempel och övningar

Två punkter a och 'har centralsymmetri När det gäller en punkt eller när AA -segmentet "går igenom det och är också mittpunkten för AA". Till punkten eller kallas Symmetricentrum.

Den centrala symmetriken för en ABC -triangel med avseende på en punkt eller är en annan triangel a'b'c 'som har följande egenskaper:

-Homologa segment är lika längd 

-Deras motsvarande vinklar har samma mått.

Figur 1. ABC Triangle och dess symmetriska a'b'c '. Källa: f. Zapata.

I figur 1 en ABC -triangel (röd) och dess centrala symmetriska a'b'c '(grön), med avseende på mitten av symmetri eller. 

I samma siffra skulle en uppmärksam observatör inse att samma resultat erhålls genom att tillämpa en original triangelrotation, så länge den är 180 ° och fokuseras på eller.

Därför motsvarar en central symmetri en 180º -sväng med avseende på symmetriens centrum.

[TOC]

Egenskaper i central symmetri

En central symmetri har följande egenskaper:

-Symmetricentret är mittpunkten för segmentet som går med i en punkt med sin symmetriska.

-En symmetrisk punkt för en annan som ligger i symmetricentret, sammanfaller med symmetriens centrum.

-Den centrala symmetriken för en triangel är en kongruent triangel (lika) med originalet.

-Bilden genom central symmetri av en omkrets är en annan omkrets av lika radie.

-En cirkel har central symmetri med avseende på sitt eget centrum.

figur 2. Design med central symmetri. Källa: Pixabay.

-Ellips har central symmetri med avseende på dess centrum.

-Ett segment har central symmetri med avseende på dess mittpunkt.

-Den liksidiga triangeln har ingen central symmetri med avseende på dess centrum, eftersom dess symmetriska, även om den är kongruent för den första, ger en liksidig triangel vän.

Det kan tjäna dig: y = 3sen (4x) funktionsperiod

-Squares har central symmetri med avseende på deras centrum.

-En Pentagon saknar central symmetri med avseende på dess centrum.

-Regelbundna polygoner har central symmetri när de har ett antal vridmomentsidor.

Exempel

Symmetrikriterierna har många tillämpningar inom vetenskap och teknik. Central symmetri finns i naturen, till exempel iskristaller och spindelnät har den här typen av symmetri.

Dessutom löses många problem lätt när förekomsten av central symmetri och andra typer av symmetri används. Därför är det bekvämt att identifiera sig snabbt när det inträffar.

Figur 3. Iskristaller har central symmetri. Källa: Pixabay.

Exempel 1

Med tanke på en punkt P av koordinater (A, B) måste du hitta koordinaterna för dess symmetriska P 'beträffande ursprunget eller koordinaterna (0, 0).

Det första är att bygga p 'p', för vilken en linje ritas som passerar genom ursprunget eller och genom punkt P. Ekvationen för denna linje är y = (b/a) x.

Låt oss nu ringa (a ', b') koordinaterna för den symmetriska punkten p '. Point P. Dessutom måste OP -avståndet vara lika med OP ', som analytiskt skriver så här:

√ (a² + b²) = √ (a '² + B² )

Följande är att ersätta b '= [(b/a).A '] i det tidigare uttrycket och fyrkant på båda sidor av jämlikhet för att eliminera kvadratroten: (a² + b²) = [a '² + (b²/till²).till'²]

Genom att extrahera gemensam faktor och förenkla nås det till '² = a². Denna ekvation har två verkliga lösningar: a '= +a eller a' = -a. 

För att få B 'använder vi igen B' = (B/A) A '. Om den positiva lösningen av A byts ut nås den att B '= B. Och när den negativa lösningen ersätts, sedan B '= -b. 

Kan tjäna dig: Vilka är de sju elementen i omkretsen?

Den positiva lösningen ger för P 'samma punkt P, så den utesluts. Den negativa lösningen erbjuder definitivt koordinaterna för den symmetriska punkten:

P ': (-a, -b)

Exempel 2

Det krävs att visa att ett AB -segment och dess symmetriska centrala A'b 'har samma längd.

Börjar med koordinaterna för punkt A, som är (AX, AY) och de i punkt B: (Bx, av), ges längden på AB av:

D (AB) = √ ((BX - AX)² + (Av - ay)² )

I analogi kommer det symmetriska segmentet a'b 'att ha längd som ges av:

d (a'b ') = √ ((bx' - ax ')² + (Av ' - ay')² )

Koordinaterna för den symmetriska punkten a 'är ax' = -ax och ay '= -ay. På samma sätt är de av B 'Bx' = -Bx och av '= -by. Om dessa koordinater ersätts i ekvationen av avstånd d (a'b ') har du:

D (a'b ') = √ ((-bx + ax)² + (-By + ay)²) som motsvarar:

 √ ((BX - AX)² + (Av - ay)²) = D (AB)

Visas att båda segmenten har samma längd.

Löst övningar

- Övning 1

Demonstrera på ett analytiskt sätt att den centrala symmetriska eller en cirkel av radie r och mitten eller, är samma ursprungliga omkrets.

Lösning

Ekvationen för en radie R och mittcirkel (0,0) är:

x² + och² = R² (Omkretsekvation c)

Om vid varje punkt P i omkretsen och koordinaterna (x, y) dess symmetriska koordinat p ') hittas, är ekvationen för den symmetriska omkretsen:

x '² + och'² = R² (Symmetrisk omkretsekvation C ')

Nu hänvisar vi till resultatet av exempel 1, som drar slutsatsen att koordinaterna för en punkt p ', symmetriska för p och koordinater (a, b), är (-a, -b). 

Men i denna övning har punkt P koordinater (x, y), så dess symmetriska p 'kommer att ha koordinater x' = -x e y '= -y. Att ersätta detta i den symmetriska omkretsekvationen är:

Kan tjäna dig: Rhomboid: Egenskaper, hur man tar ut omkretsen och området

(-X)² + (-och)² = R²

Vilket motsvarar: x²+ och² = R², drog slutsatsen att den centrala symmetriken i en cirkel med avseende på dess centrum är omkretsen själv.

- Övning 2

Demonstrera på ett geometriskt sätt att central symmetri bevarar vinklarna.

Lösning

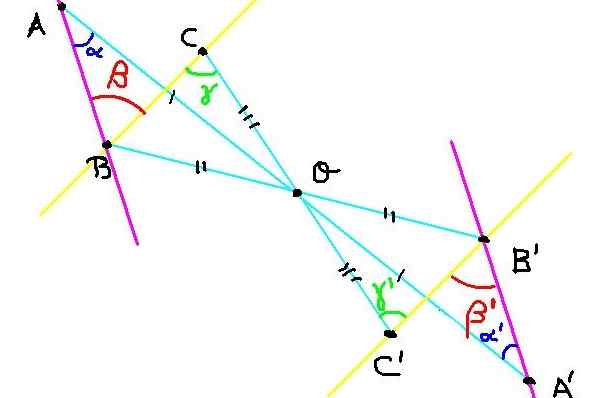Figur 4. Konstruktion av symmetriska punkter för övning 2. Källa: f. Zapata.

Det finns tre punkter A, B och C på planet. Dess symmetriska a ', b' och c 'är byggda med avseende på symmetriens centrum eller, som visas i figur 4. 

Nu måste vi visa att vinkeln ∡ABC = ß har samma mått som vinkeln ∡a'b'c '= ß' '.

Eftersom C och C 'är symmetriska, då oc = oc'. På liknande sätt ob = ob 'y oa = oa'. Å andra sidan är vinkeln ∡Boc = ∡b'oc 'för att vara emot toppen till toppen.

Då är trianglarna boc och b'oc 'kongruent för att ha en lika vinkel mellan två sidor lika.

Eftersom BOC är kongruent till B'oc 'då vinklarna  y och y ' De är lika. Men dessa vinklar, förutom att uppfylla y = y ' De är interna alternativa mellan BC- och B'C -linjerna vilket innebär att BC -linjen är parallell med B'C '.

På liknande sätt är Baa överensstämmande med B'oa 'av vad som följs det α = α ' . Men  a och α ' De är inre alternativa vinklar mellan Ba- och B'A -linjerna, av vilka det dras slutsatsen att linjen BA är parallell med B'a '.

Eftersom vinkeln ∡ABC = ß har sina parallella sidor med vinkeln ∡a'b'c '= ß' och båda är akuta är det slutsatsen att:

∡abc = ∡a'b'c '= β = β' '

Demonstrerar på detta sätt att central symmetri behåller måtten på vinklar.

Referenser

1. Baldor, J. TILL. 1973.Platt och rymdgeometri. Centralamerikansk kultur. 
2. Matematiska lagar och formler. Vinkelmätningssystem. Hämtad från: Ingemecanica.com.
3. Wentworth, g. Planetgeometri. Återhämtat sig från: Gutenberg.org.
4. Wikipedia. Centralsymmetri. Återhämtad från: är.Wikipedia.com
5. Wikipedia. Transportband. Återhämtad från: är.Wikipedia.com
6. Zapata f. Interna och externa konjugatvinklar. Hämtad från: Lifer.com