Euler nummer eller nummer e hur mycket är värt, egenskaper, applikationer

han Euler -nummer eller nummer E Det är en välkänd matematisk konstant som ofta förekommer i många vetenskapliga och ekonomiska tillämpningar, tillsammans med antalet π och andra viktiga siffror i matematik.

En vetenskaplig kalkylator kastar följande värde för nummer E:

Figur 1. Eulers nummer visas ofta inom vetenskapen. Källa: f. Zapata.

E = 2.718281828 ..

Men många fler decimaler är kända, till exempel:

E = 2.71828182845904523536 ..

Och moderna datorer har tillåtit decimal biljoner till numret E.

Det är ett nummer irrationell, Vilket innebär att den har en oändlig mängd decimaler utan något repetitivt mönster (sekvens 1828 visas två gånger i början och inte längre upprepar).

Och det betyder också att antalet E inte kan erhållas som kvoten på två hela siffror.

[TOC]

Historia

Numret och Han identifierades av forskaren Jacques Bernoulli 1683 när han studerade problemet med sammansatt intresse, men tidigare hade han indirekt dykt upp i verk av den skotska matematikern John Napier, som uppfann logaritmerna för 1618.

Men det var Leonhard Euler 1727 som gav honom numret E -namnet och intensivt studerade sina egenskaper. Det är därför det också är känt som Eulernummer och också som en naturlig grund för de neperiska logaritmerna (en exponent) som används.

Hur mycket är antalet E är värt?

Numret E Vale:

E = 2.71828182845904523536 ..

De suspensiva punkterna innebär att det finns en oändlig mängd decimaler och i själva verket är miljoner av dem kända med nuvarande datorer.

Representationer av nummer E

Det finns flera sätt att definiera E som vi beskriver nedan:

Antalet E som en gräns

Ett av de olika sätten på vilka antalet E uttrycks är den som forskaren Bernoulli hittade i sitt arbete med sammansatt intresse:

Där du måste göra värdet n Ett mycket stort antal.

Det är lätt att kontrollera, med hjälp av en räknare, att när n Det är mycket stort, det tidigare uttrycket tenderar till värdet av och ovanstående.

Det kan tjäna dig: Bijjektiv funktion: Vad är det, hur görs det, exempel, övningar

Naturligtvis kan vi fråga oss hur stort det kan göras n, Så vi försöker med runda nummer, till exempel dessa: till exempel:

n = 1000; 10.000 eller 100.000

I det första fallet får du E = 2.7169239 .. . I den andra E = 2.7181459 ... och i det tredje är det mycket mer nära värdet av och: 2.7182682. Vi kan redan dyka upp som med n = 1.000.000 eller större, tillvägagångssättet blir ännu bättre.

På matematiskt språk, förfarandet för att göra n Det blir närmare och mer till ett mycket stort värde, det kallas Begränsning till oändlighet Och det betecknas så här:

För att beteckna oändligheten används symbolen "∞".

Numret E som en summa

Det är också möjligt att definiera nummer E genom denna operation:

Siffrorna som visas i nämnaren: 1, 2, 6, 24, 120 ... motsvarar operationen n!, var:

n! = n. (N-1).(N-2). (N-3) ..

Och per definition 0! = 1.

Det är lätt att verifiera att ju fler tillägg läggs till, desto större antal nås och.

Låt oss göra några tester med räknaren och lägga till allt mer tillägg:

1 +1+ (1/2) + (1/6) = 2.71667

1 +1+ (1/2) + (1/6) + (1/24) = 2.75833

1 +1+ (1/2) + (1/6) + (1/24) + (1/120) = 2.76667

1 +1+ (1/2) + (1/6) + (1/24) + (1/120) + (1/720) = 2.71806

Ju fler termer de läggs till i summan, desto mer liknar resultatet och.

Matematiker utformade en kompakt notation för dessa summor som involverar många termer, med hjälp av sumssymbolen σ:

Detta uttryck läses som "summa av n = 0 till oändligheten av 1 mellan n factorial".

Antalet E från den geometriska synvinkeln

Antalet E har en grafisk representation relaterad till området under diagrammet för kurvan:

y = 1/x

När värdena på X är mellan 1 och E är detta område värt 1, såsom illustreras i följande figur:

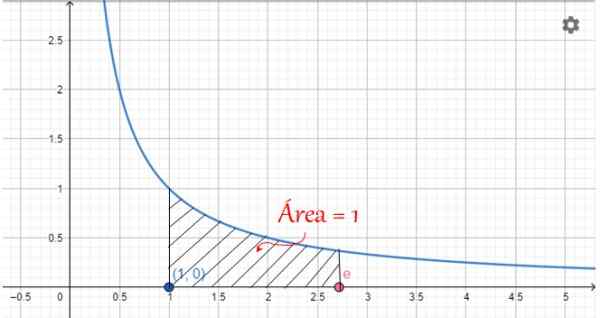figur 2. Grafisk representation av antal E: Området under kurvan 1/x, mellan x = 1 och x = E. Källa: f. Zapata.

Antal E -egenskaper

Några av egenskaperna för nummer E är:

Kan tjäna dig: Växande funktion: Hur man identifierar den, exempel, övningar

-Det är irrationellt, med andra ord, det kan inte erhållas helt enkelt genom att dela två hela siffror.

-Numret och Det är också en Transcendent nummer, vilket betyder att och Det är inte en lösning av någon polynomekvation.

-Det är relaterat till fyra andra kända nummer inom matematikområdet, nämligen: π, i, 1 och 0, genom Euler: s identitet:

och^πi + 1 = 0

-Samtal komplexa tal kan uttryckas genom E.

-Det utgör grunden för naturliga eller neperiska logaritmer idag (John Napiers ursprungliga definition skiljer sig lite).

-Det är det enda numret som dess Neperian logaritm är värt 1, det vill säga:

 ln e = 1

Ansökningar

Statistik

Antalet E visas mycket ofta inom området för sannolikhet och statistik, som förekommer i olika distributioner, till exempel det normala eller gaussiska, det av Poisson och andra.

Teknik

Inom teknik är det ofta, eftersom den exponentiella funktionen y = e^x Det finns till exempel i mekanik och elektromagnetism. Bland de många ansökningarna kan vi citera:

-En kabel eller kedja som hänger med förbehåll för ändarna, antar formen på kurvan som ges av:

y = (e^x + och^-x) /2

-En kondensor C ursprungligen utskriven, som i serie ansluter till ett motstånd R och en spänningskälla V för att ladda, förvärvar en viss belastning q beroende på tiden t som ges av:

Q (t) = cv (1-e^-T/rc)

biologi

Exponentiell funktion y = a.och^Bx, Med A- och B -konstant används den för att modellera celltillväxt och bakterietillväxt.

Fysisk

I kärnfysik modelleras det radioaktiva förfallet och bestämningen av åldrar av radiokolon daterad.

Ekonomi

Vid beräkningen av sammansatt intresse uppstår antalet E naturligt.

Anta att du har en viss summa pengar P_antingen, att investera det till en årlig ränta.

Om pengarna är kvar i 1 år, kommer du efter den tiden:

P (1 år) = P_antingen + P_antingen.i = p_antingen (1+ i)

Efter ytterligare ett år utan att röra vid det kommer du att ha:

Kan tjäna dig: Teoretisk sannolikhet: Hur man får ut det, exempel, övningar

P (2 år) = P_antingen + P_antingen.I + (P_antingen + P_antingen .i) i = p_antingen +2 p_antingen.i + p_antingen.Yo²  = PO (1+i)²

Och på detta sätt förbi n år:

P = p_antingen (1+i)ⁿ

Kom ihåg en av definitionerna av E:

Det ser lite ut som uttrycket för p, så det måste finnas en relation.

Vi kommer att dela ut den nominella räntan Yo i n Tidsperioder, på detta sätt kommer den sammansatta räntan att vara I/N:

P = p_antingen [1+ (I/N)]ⁿ

Detta uttryck ser lite mer ut om vår gräns, men det är ännu inte exakt samma.

Men efter vissa algebraiska manipulationer kan det visas att göra denna förändring av variabel:

h = n/i → i = n/h

Våra pengar P blir:

P = p_antingen [1+ (1/h)]^Hej = P_antingen [1+ (1/h)]^hYo

Och vad som är bland nycklarna, även om det är skrivet med brevet h, Det är lika med argumentet från gränsen som definierar antalet E, saknas bara att ta gränsen.

Låt oss göra  h → ∞, och vad som är mellan nycklarna omvandlas till numret och. Detta betyder inte att vi måste vänta en oändligt stor tid för att dra tillbaka våra pengar.

Om vi ​​ser bra ut när vi gör det H = n/i Och att tendera till ∞, vad vi verkligen har gjort är att fördela räntan under mycket, mycket små perioder: mycket liten:

I = n/h

Det här kallas Kontinuerlig kapital. I detta fall beräknas mängden pengar enkelt enligt följande:

P = p_antingen .och^Yo

Där jag är den årliga räntan. Till exempel genom att deponera 12 till 9 % per år, genom kontinuerligt aktivering, efter ett år har du:

P = 12 x e^{0.09 × 1} € = 13.13 €

Med en vinst på 1.13 €.

Referenser

1. Njut av matematik. Sammansatt ränta: periodisk sammansättning. Återhämtat sig från: njutmatimaticas.com.
2. Figuera, J. 2000. Matematik 1: a. Diversifierad. Co-bo-utgåvor.
3. Garcia, m. Numret E i den elementära beräkningen. Återhämtat sig från: matematik.Ciens.Ucv.gå.
4. Jiménez, r. 2008. Algebra. Prentice hall.
5. Larson, r. 2010. Beräkning av en variabel. 9na. Utgåva. McGraw Hill.