Kvantantal för vad som används och vad som är

De nKvantuttagare De används för att beskriva kvanttillståndet för elektronerna i atomen och har sitt ursprung i lösningen av Schrödinger -ekvationen för den enklaste av alla: väte.

Schrödingers ekvation är en differentiell ekvation, vars lösningar är Vågfunktioner och de betecknas av den grekiska bokstaven ψ. Oändliga lösningar kan höjas, och dess kvadrat motsvarar sannolikheten för att hitta elektronen i en liten rymdregion, kallad omlopps-.

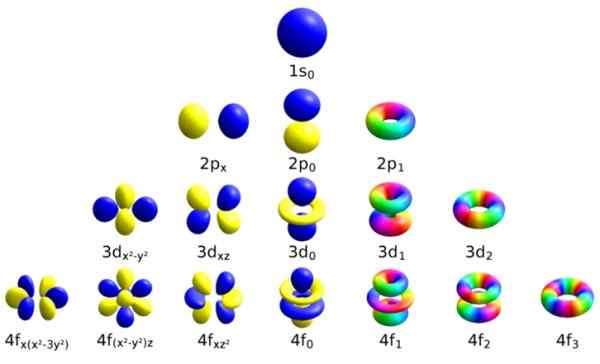
Var och en av dessa atomorbitaler kännetecknas av en viss uppsättning kvantantal. Källa: Wikimedia Commons.

Varje orbital har definierade egenskaper som skiljer den från andra, såsom energi, vinkelmoment och snurr, en helt kvantegenskap hos elektronen och som är ansvarig bland annat för magnetiska effekter.

Sättet att identifiera varje omlopp är att skilja den genom en uppsättning siffror som beskriver det, och dessa är just kvantantalet:

-N: är det viktigaste kvantantalet.

-ℓ: Det azimutala kvantantalet.

-m_ℓ, Det är det magnetiska antalet.

-m_s, Snurrnumret.

[TOC]

Vad är kvantantal för?

Kvantantal tjänar till att beskriva tillståndet för elektroner inuti atomen. Den atomiska modellen där elektronen vänder runt kärnan är felaktig, eftersom den inte överensstämmer med atomstabilitet eller med ett stort antal fysiska fenomen observerade.

Det är därför danska niels Bohr (1885-1962) gjorde 1913 ett djärvt förslag: elektronen kan bara hittas i vissa stabila banor, vars storlek beror på ett heltal som heter N.

Senare, 1925, höjde den österrikiska fysiska Erwin Schrödinger (1887-1961) en differentiell ekvation i partiella derivat, vars lösningar beskriver väteatomen. Är vågfunktionerna ψ nämns i början.

Denna differentiella ekvation inkluderar de tre rumsliga koordinaterna plus tid, men när den inte ingår är lösningen av Schrödinger -ekvationen analog med en stationär våg (en våg som sprider sig mellan vissa gränser).

Vågfunktioner

Schrödingers oberoende tidsekvation löses i sfäriska koordinater och lösningen är skriven som produkten av tre funktioner, en för varje rumslig variabel. I detta koordinatsystem istället för att använda koordinaterna för de kartesiska axlarna x, och och z Koordinater används r, θ och φ. Den här vägen:

Kan tjäna dig: parallell krets

ψ (r, θ, φ) = r (r) ⋅f (θ) ⋅g (φ)

Vågfunktionen är immateriell, trots kvantmekanik säger den oss att fyrkantig amplitud:

| ψ (r, θ, φ) |²

Det vill säga att modulen eller det absoluta värdet på vågfunktionen, kvadrat, är ett verkligt antal som representerar sannolikheten för att hitta elektronen, i en viss region runt den punkt vars koordinater är r, θ och φ.

Och detta faktum är något mer konkret och konkret.

För att hitta vågfunktionen måste du lösa tre vanliga differentiella ekvationer, en för varje variabel r, θ och φ.

Lösningarna för varje ekvation, som kommer att vara funktionerna r (r), f (θ) och g (φ), innehåller de första tre nämnda kvantumret.

Vilka är kvantnumren?

Nedan beskriver vi kort arten av varje kvantantal. De tre första, som nämnts ovan, härrör från lösningarna från Schrödinger -ekvationen.

Det fjärde numret lades till av Paul Dirac (1902 - 1984) 1928.

Huvudantal

Det betecknas av n och indikerar storleken på den tillåtna omloppet såväl som elektronens energi. Ju högre dess värde, desto mer är kärnens elektron och dess energi också, men i gengäld minskar den dess stabilitet.

Detta nummer uppstår från R (R) -funktionen, vilket är sannolikheten för att hitta elektronen på ett visst avstånd r av kärnan, som bestäms av:

 Där följande konstanter deltar:

-Planck Constant: H = 6,626 × 10 ^{-3. 4} J.s
-Elektronmassa m_och = 9.1 × 10^-31 kg
-Elektronbelastning: E ​​= 1.6 × 10^-19 C.
-Elektrostatisk konstant: K = 9 × 10 ⁹ N.m²/C²

När n = 1 motsvarar BOHR -radien som är värd cirka 5.3 × 10⁻¹¹ m.

Förutom det första lagret är de andra indelade i underkapslar eller underavtal. Varje lager har en energi i Volt Electron som ges av:

Kan tjäna dig: mekaniska vågor: egenskaper, egenskaper, formler, typer

Termen Ev "Electron Volt" betyder, energienheten som används ofta inom kvantfysikområdet. Där n = 1, 2, 3, 4 .. . och varje n -värde motsvarar a lager, som är märkt med stora bokstäver:

• K (n = 1)
• L (n = 2)
• M (n = 3)
• N (n = 4)
• Eller (n = 5)
• P (n = 6)
• Q (n = 7).

I teorin finns det ingen övre gräns för N, men i praktiken observeras det att det bara når n = 8. Den minsta möjliga energin motsvarar n = 1 och är den för Grundtillstånd.

Azimutalt kvantantal eller vinkelmoment

Det här antalet, detta nummer, bestämmer formen på orbitalerna, när man kvantifierar storleken på elektronens omloppsvinkelmoment.

Du kan till exempel ta hela och positiva värden mellan 0 och N-1:

-När n = 1, då ℓ = 0 och det finns en enda undernivå.

-Om n = 2, kan ℓ vara värt 0 eller 1, så du har två underavtal.

-Och om n = 3, antar ℓ värden 0, 1 och 2 och det finns 3 underavtal.

Det kan följas på obestämd tid, även om det i praktiken n når upp till 8. Sub -nivåer betecknas genom bokstäver: s, p, d, F och g Och de ökar i energi.

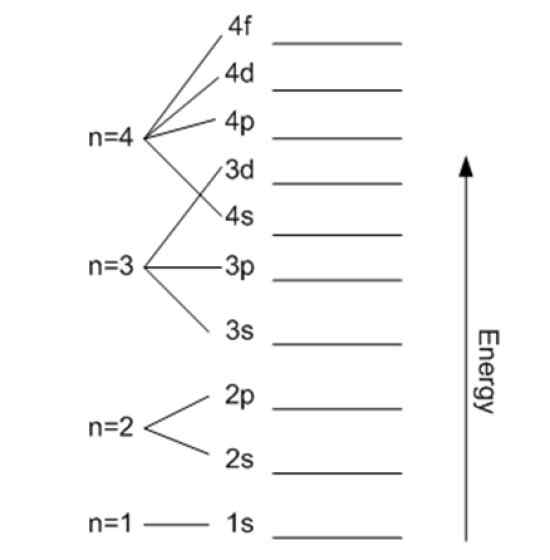Energi är relaterad till det viktigaste kvantantalet. Källa: Wikimedia Commons.

Magnetiskt kvantantal m_ℓ

Detta antal avgör orienteringen av orbitalet i rymden och dess värde beror på ℓ.

För en given ℓ finns det (2ℓ+1) hela värden på M _ℓ, motsvarande respektive orbitaler. Dessa är:

-ℓ, ( - ℓ+1), ... 0, ... (+ℓ -1),+ℓ.

Exempel

Om n = 2, vet vi att ℓ = 0 och ℓ = 1, då m _ℓ Ta följande värden:

-För ℓ = 0: m _ℓ = 0.
-För ℓ = 1: m _ℓ = -1, m _ℓ = 0, m _ℓ = +1

Orbital n = 2 har två sub -nivåer, den första med n = 2, ℓ = 0 och m _ℓ = 0. Sedan har vi den andra sub -nivån: n = 2, ℓ = 1, med 3 orbitaler:

• N = 2, ℓ = 1, m _ℓ = -1
• N = 2, ℓ = 1, m _ℓ = 0
• N = 2, ℓ = 1, m _ℓ = +1

De tre orbitalerna har samma energi men olika rumsliga orientering.

Kvantantal spin m_s

Vid lösning av Schrödinger -ekvationen i tre dimensioner uppstår de redan beskrivna siffrorna. I väte observeras emellertid en ännu mer struktur än dessa siffror räcker inte för att förklara.

Det kan tjäna dig: Gase Constant: Vad är, beräkning och exempel

1921 föreslog därför en annan kroppsbyggnad, Wolfgang Pauli, förekomsten av ett fjärde nummer: spinnnumret M_s, som tar värden på +½ eller -½.

Med detta nummer beskrivs en mycket viktig egenskap hos elektronen, vilket är snurra, ord som kommer från engelska snurra (Vänd dig själv). Och snurret är i sin tur relaterad till atomens magnetiska egenskaper.

Ett sätt att förstå snurret är att föreställa sig att elektronen uppför sig som en liten magnetisk dipol (en magnet med nord- och sydpoler), tack vare en rotation runt sin egen axel. Svängen kan vara i samma riktning som klocknålarna, eller i motsatt riktning.

Även om Pauli föreslog förekomsten av detta nummer, hade resultaten från ett experiment som genomfördes av Otto Stern och Walter Gerlach 1922 redan förväntat det.

Dessa forskare lyckades dela en stråle av silveratomer genom applicering av ett icke -enhetligt magnetfält.

Värdet på m_s Det beror inte på n, ℓ och m _ℓ. Grafiskt representeras det av en pil: en pil uppåt indikerar schemat och en nedåt antihoran.

Pauli uteslutningsprincip

Beteendet hos elektroner i atomen sammanfattas i principen om uteslutning av Pauli, som säger att två elektroner av en atom inte kan existera i samma kvanttillstånd.

Därför måste varje elektron ha en annan uppsättning kvantantal n, ℓ, m _ℓ och M_s.

Betydelsen av kvantantal och denna princip ligger i förståelsen av egenskaperna hos elementen i periodiska tabellen: elektronerna är organiserade i lager enligt N, och sedan i underkroppar enligt ℓ och resten av siffrorna.

Referenser

1. Alonso, m. 1971. Kvant- och statistiska grunder. Interamerikansk utbildningsfond.
2. Bauer, w. 2011. Fysik för teknik och vetenskap. Volym 1. MC Graw Hill.
3. Chang, R. 2013. Kemi. 11VA. Utgåva. MC Graw Hill Education.
4. Eisberg-resnick. 1989. Kvantfysik. Limusa - Wiley.
5. Giambattista, a. 2010. Fysik. 2: a. Ed. McGraw Hill.
6. Rex, a. 2011. Fysikens grunder. Pearson.
7. Tippens, s. 2011. Fysik: koncept och applikationer. Sjunde upplagan. McGraw Hill.