Udda tal

Vad är udda nummer?

De udda tal De är de hela siffrorna som inte är delbara med 2. Detta innebär att du med udda mängder inte kan göra grupper av en 2, till exempel om någon har 9 godisar att dela med en vän och inte vill dela några, kommer de att röra 4 godisar och de andra 5.

Några av de udda siffrorna är följande: ... -5, -3, -1, 1, 3, 5, 7, 9, 11, 13 ..  I detta uttryck indikerar de suspensiva punkterna att det finns fler siffror, både vänster och höger.

Bild 1: Hur man vet om ett nummer är udda?

Ser man noggrant kan du se att varje udda nummer kan erhållas genom att lägga till 2 till föregående nummer. Om vi ​​till exempel lägger till 2 till -1 får du 1, om vi gör 1 + 2 är det 3 och så vidare.

Det observeras också att om paren är isär, inklusive 0, som betraktas som ett jämnt nummer, erhålls uppsättningen av hela siffror Z.

Det är därför något udda naturliga nummer kan skrivas i formen 2n + 1, där n = 0, ± 1, ± 2, ± 3, ± 4, ± 5 ..., där symbolen ± betyder att den kan tas som positiv eller så negativt.

När det gäller större antal kan det erkännas när det är en udda, eftersom det alltid slutar i 1, 3, 5, 7 eller 9. Till exempel är 1571 udda och så är det negativa heltalet -152.489.

Exempel på udda nummer

De udda siffrorna presenteras ofta i naturen, och bland dem är nummer 3 av särskild betydelse. Låt oss titta på några exempel:

-Det finns många blommor med ett udda antal kronblad.

-Vi har 5 fingrar i varje hand.

Kan tjäna dig: slumpmässig variabel: koncept, typer, exempel

-Människor har 23 kromosomer par.

-Det finns de tre lagarna i Newton och de tre lagarna i termodynamik.

-Kärnorna i atomerna som har ett udda antal protoner och neutroner är mindre stabila än de med ett parnummer.

-Magi är 3.

-I berättelser och berättelser visas nummer 3 ofta, till exempel romaner som De tre musketörerna av Alejandro Dumas och i populära berättelser som De tre bröderna och De tre små grisarna.

-För den konstnärliga sammansättningen finns det samtalet Udda regel, som konstaterar att en sammansättning med ett udda antal element är mer attraktiv än ett med ett par. Det udda numret lägger till dynamik, medan ett par ger stabilitet.

figur 2. Ett udda antal element lägger dynamik till en bild

-En vanlig strategi för att få objektpriser att se billigare ut är att hamna 9, till exempel 2.$ 99, $ 39 och så vidare.

-Numret 13 betraktas som otur av vissa, medan andra tillskriver mystiska egenskaper till 11, båda udda siffrorna.

Primo -nummer

Primo -nummer, de som bara erkänner som delare själva och 1, är udda, med undantag för 2, vilket är det enda kusinnummermomentet.

Det är möjligt att visa att valfritt antal kan brytas ned som en produkt av främsta faktorer (inklusive dessa krafter), och att detta sätt att uttrycka antalet är unikt, utom i faktorens ordning.

Till exempel kan nummer 45 brytas ned som 45 = 3³ x 5.

Udda nummeroperationer

Med de udda siffrorna utförs alla aritmetiska operationer, och vissa har enastående egenskaper.

Kan tjäna dig: symbolisering av uttryck

- Summor och produkter

-Summan av två udda siffror resulterar i ett jämnt nummer: 3+5 = 8; 11+15 = 26; (-10)+ (+6) = - 4.

-Genom att lägga till ett udda nummer med ett vridmoment är resultatet udda: 7+2 = 9; 26+ 9 = 35; (-5) + 12 = 7.

-Om n Första naturliga, udda och på varandra följande nummer är resultatet n². Låt oss se detta med lite mer detalj:

För n = 2: 1 + 3 = 4 = 2²

För n = 3: 1 + 3 + 5 = 9 = 3²

För n = 4: 1 + 3 + 5 + 7 = 16 = 4²

-När en udda multipliceras med ett par uppstår ett jämnt nummer: 7 x 4 = 28; (-3) x 12 = -36.

-Multiplicera två udda siffror erhålls också en udda: 3 x 5 = 15; (-5) x (+11) = -55.

- Mak

-När ett positivt antal höjs till en udda kraft är det ett positivt tal, till exempel: 3³ = 27.

-Genom att höja ett negativt tal till en udda kraft är resultatet negativt: (-2)³= (-2) x (-2) x (-2) = -8.

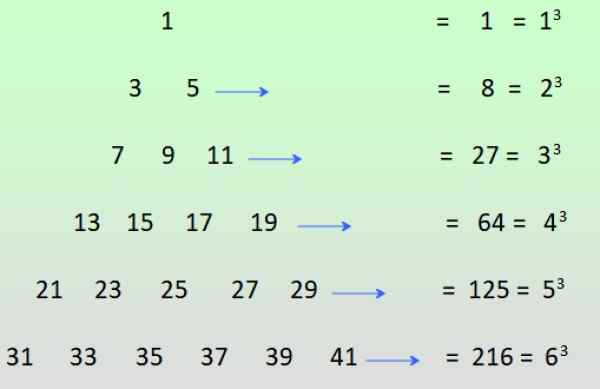
-Udda krafter hos positiva heltal kan uppnås om udda siffror finns tillgängliga som visas i figuren och raderna läggs till:

Figur 3. Att få de udda krafterna från summan av udda siffror. Källa: f. Zapata.

Löst övningar

- Övning 1

Bestäm om resultatet av följande operation är jämnt eller udda:

(53476890083 + 1987628967) x 13567903

Lösning

För att få svaret behöver du inte springa för att leta efter en räknare, utan för att tillämpa egenskaperna som ses. Låt oss titta på de sista siffrorna i tillägg, som är 3 respektive 7:

53476890083  + 1987628967

Detta innebär att missbrukarna är udda och vi vet redan att summan av två udda siffror är jämn.

Därför är siffran som är resultatet av parentesen jämn och vi kommer att multiplicera med ett nummer som slutar i 3:

Kan tjäna dig: vektoralgebra

13567903

Vilket innebär att detta nummer är udda.

I de egenskaper som beskrivs ovan konstaterades att det är ett jämnt antal att multiplicera vridmoment x. Därför är den resulterande operationen jämn.

- Övning 2

Hur mycket är summan av de första 5 på varandra följande udda siffrorna? Och den av de första 50?

Lösning

Summan av de första 5 på varandra följande udda siffrorna är:

1 + 3 + 5 + 7 + 9 = 25

Men om vi vill lägga till de första 50 på detta sätt är det besvärligt, så vi går till egenskaperna. De bekräftar att summan av på varandra följande udda siffror är n². I detta fall är N = 50 och den begärda beloppet:

femtio² = 50 x 50 = 2500.

- Övning 3

När tre på varandra följande udda nummer läggs till, erhålls 237. Vilka är siffrorna??

Lösning

Låt oss ringa vårt första udda nummer, och det andra och z till det tredje, enligt uttalandet är det uppfyllt att:

x + y + z = 237

På algebraiskt språk kan alla udda nummer skrivas i formen 2n +1. Låt oss göra vårt första udda nummer:

x = 2n +1

Låt oss lägga till 2 för att få följande udda:

y = x + 2 = (2n + 1) + 2 = 2n + 3

Och slutligen läggs det till igen 2 för att få den tredje udda:

Z = (2n +3) + 2 = 2n + 5

Allt detta lägger till:

2n + 1 + 2n + 3 + 2n + 5 = 237

6n + 9 = 237

Det resulterar i en enkel linjär ekvation, vars lösning är:

n = 38

Och nu med värdet av n = 38 finns det de tre beställningarna:

x = (2 × 38) + 1 = 77

Följande är därför udda i följd:

y = 79

Z = 81

Och läsaren kan enkelt verifiera att summan av de tre är 237.

Referenser

1. Baldor, a. 1986. Aritmetisk. Codex -utgåvor och distributioner.
2. Stadsdelar, L. De udda siffrorna och krafterna i naturliga siffror. Hämtad från: Sinewton.org.
3. Lysande. Även och udda siffror. Återhämtat sig från: lysande.org.
4. Matematik 18. Udda nummeroperationer. Hämtad från: Matematik18.com.
5. Wikipedia. Även och udda siffror. Återhämtad från: är.Wikipedia.org.