Transcendenta nummer som är, formler, exempel, övningar

De transcendenta nummer De är de som inte kan erhållas till följd av en polynomekvation. Motsatsen till ett transcendent nummer är ett algebraisk nummer, som är lösningar av en polynomekvation av typen:

till_n xⁿ + till_N-1 x^N-1 +... + a₂ x² + till₁ x + a₀ = 0

Där koefficienterna till_n, till_N-1,Till ... till₂, till₁, till₀ De är rationella nummer som kallas polynomkoefficienter. Om ett X -nummer är en lösning av föregående ekvation, är det antalet inte transcendenta.

Figur 1. Två antal stora betydelser i vetenskapen är transcendenta siffror. Källa: Public DomainPartures.netto.

Vi kommer att analysera några nummer och se om de är transcendenta eller inte:

a) 3 är inte transcendent eftersom det är en lösning av x - 3 = 0.

b) -2 kan inte vara transcendent eftersom det är en lösning av x + 2 = 0.

c) ⅓ Det är 3x - 1 = 0 -lösning

d) en lösning av ekvation x² - 2x + 1 = 0 är √2 -1, så nämnda nummer per definition är inte transcendent.

e) inte heller √2 eftersom det är resultatet av ekvation x² - 2 = 0. Genom att höja √2 kvadrat resulterar det i 2, som subtraheras från 2 spelar ingen roll till noll. Så √2 är ett irrationellt antal men det är inte transcendent.

[TOC]

Vad är transcendenta nummer?

Problemet är att det inte finns någon allmän regel för att få dem (senare kommer vi att säga ett formulär), men några av de mest kända är numret pi och den Nepernummer, betecknad respektive av: π och och.

Numret π

Numret π Naturligtvis verkar det naturligtvis att den matematiska kvoten mellan omkretsen P i en cirkel och dess diameter D, oavsett om det är en liten eller stor cirkel, alltid ger samma nummer som kallas pi:

π = P/D ≈ 3 14159 ..

Detta innebär att om omkretsens diameter tas som en mätenhet, för dem alla, oavsett om de är stora eller små, kommer omkretsen alltid att vara värd p = 3,14 ... = π, Som framgår av animationen av figur 2.

Kan tjäna dig: bolzano teorem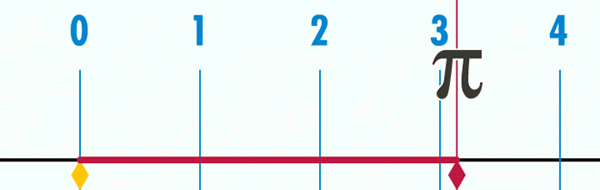figur 2. Cirkelns omkretsslängd är ibland längden på diametern och är ungefär 3.1416.

För att bestämma fler decimaler måste du mäta mer precision P och D och sedan beräkna kvoten, vilket har gjorts på matematiskt sätt. Slutsatsen är att kvotens decimaler inte har något slut och aldrig upprepas, så antalet π Förutom att vara transcendent är det också irrationell.

Ett irrationellt antal är det antal som inte kan uttryckas som uppdelningen av två hela siffror. 

Det är känt att varje transcendent nummer är irrationellt, men det är inte sant att alla irrationella är transcendenta. Till exempel √2 är irrationellt, men det är inte transcendenta.

Figur 3. Transcendenta siffror är irrationella, men ömsesidiga uttalande är inte sant.

Numret E

Det transcendenta numret är grunden för de neperiska logaritmerna och deras decimalstrategi är:

E ≈ 2.718281828459045235360 .. .

Om du ville skriva numret och Exakt, skulle det vara nödvändigt att skriva decimal oändligt, eftersom varje transcendent antal är irrationella, som sagt tidigare.

De första tio siffrorna i och De är lätta att komma ihåg:

2.7 1828 1828 och även om det verkar följa ett repetitivt mönster, uppnås detta inte i ordningens decimaler större än nio.

En mer formell definition av och är nästa:

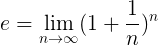
Vilket innebär att det exakta värdet på och Den operation som anges i denna formel uppnås när det naturliga antalet n Det tenderar att oändligt.

Detta förklarar varför vi bara kan få tillvägagångssätt till och, Eftersom hur stort numret n är placerat, kan du alltid hitta en n äldre.

Låt oss leta efter några tillvägagångssätt på egen hand:

-När n = 100 sedan (1 + 1/100)¹⁰⁰ = 2 70481 som knappt sammanfaller i den första decimalen med det "sanna" värdet av E.

-Om du är vald n = 10.000 du har (1 + 1/10.000)^10.000 = 2 71815 som sammanfaller med det "exakta" värdet av E i de första tre decimalerna.

Kan tjäna dig: homologa sidor

Denna process bör följas för att kunna få det "sanna" värdet på E. Jag tror inte att vi har tid att uppnå det, men låt oss göra ytterligare ett försök:

Låt oss använda n = 100.000:

(1 + 1/100.000)^100.000 = 2.7182682372

Att det bara har fyra decimaler som sammanfaller med det betraktade värdet.

Det viktiga är att förstå att desto större är värdet på n som valts att beräkna och_n, Närmare kommer att vara av det verkliga värdet. Men det verkliga värdet kommer bara att hållas när N är oändligt.

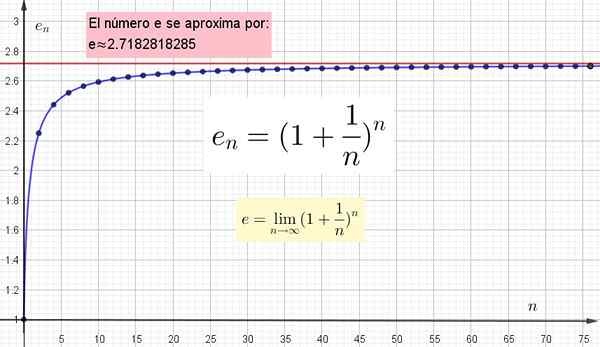Figur 4. Det visas grafiskt eftersom det högre värdet på n är närmare E, men för att nå det exakta värdet n måste vara oändligt.

Andra transcendenta nummer

Bortsett från dessa berömda nummer finns det till exempel andra transcendenta nummer: till exempel:

- 2^√2

Alla algebraiska antal, som inte är 0 eller 1, förhöjda till en irrationell exponent kommer att vara ett transcendent nummer.

-Champernownes nummer 10: 

C_10 = 0.12345678910112131415161718192021 .. .

-Champernownes nummer på bas 2:

C_2 = 0.110111001011011 .. .

-Γ eller konstant gammanalet Euler-Mascheroni:

γ ≈ 0,577 215 664 901 532 860 606

Det erhålls genom att göra följande beräkning:

y ≈ 1 + ½ + ⅓ + ¼ + ... + 1/n - ln (n)

När n vara mycket stor. För att ha det exakta värdet på gammanumret skulle det vara nödvändigt att beräkna med n oändlig. Något liknande det vi gjorde ovan.

Och det finns många fler transcendenta nummer. Den stora matematikern Georg Cantor, född i Ryssland och bodde mellan 1845 och 1918, visade att uppsättningen av transcendenta siffror är mycket större än uppsättningen av algebraiska siffror.

Formler där det transcendenta numret π visas

Omkretsen av omkretsen

P = π d = 2 π r, där p är omkretsen, d diametern och r omkretsens radie. Det bör komma ihåg att:

Kan tjäna dig: Hur mycket har du att lägga till 3/4 för att få 6/7?

-Omkretsens diameter är det längsta segmentet som förenar två punkter av det och som alltid passerar genom dess centrum,

-Radie är hälften av diametern och är det segment som går från mitten till kanten.

Cirkelområde

A = π r² = ¼ π d²

En sfär

S = 4 π r^2.

Ja. Även om det inte verkar är ytan på en sfär densamma som för fyra cirklar av samma radie som sfären.

Sfärvolym

V = 4/3 π r³

Övningar

- Övning 1

Den "exotiska" pizzeria säljer tre diameter pizzor: 30 cm liten, median 37 cm och stora 45 cm. Ett barn är mycket hungrig och insåg att två små pizzor har samma kostnad som en stor. Vad blir bättre för honom, köp två små pizzor eller en stor?

Figur 5.- Området för en pizza är proportionell mot radien och är proportionalitetskonstanten. Källa: Pixabay.

Lösning

Ju större området, desto större är mängden pizza, av detta skäl kommer området för en stor pizza att beräknas och jämföras med två små pizzor:

Stort pizzaområde = ¼ π d² = ¼ ⋅3,1416⋅45² = 1590,44 cm²

Liten pizza = ¼ π d² = ¼ ⋅3,1416⋅30² = 706,86 cm²

Därför kommer två små pizzor att ha ett område på 

2 x 706,86 = 1413,72 cm² .

Det är tydligt: ​​det kommer att finnas mer pizza som köper en enda stor än två små.

- Övning 2

Den "exotiska" pizzeria säljer också en 30 cm radie -semi -man -pizza för samma rektangulära form på 30 x 40 cm sida. Vilket skulle du välja?

Figur 6.- Ytan på en halvtalare är dubbelt så stor som basytan på basen. Källa: f. Zapata.

Lösning

Som sagt i föregående avsnitt är ytan på en sfär fyra gånger större än en cirkel med samma diameter, så en 30 cm diameter semi -spear kommer att ha:

30 cm semi -man -pizza: 1413,72 cm² (två gånger en cirkulär med samma diameter)

Rektangulär pizza: (30 cm) x (40 cm) = 1200 cm² .

Semi -Man -Pizza har ett större område.

Referenser

1. Fernández J. Numret E. Ursprung och nyfikenheter. Återhämtad från: Soy Mathematics.com
2. Njut av matematik. Eulers nummer. Återhämtat sig från: njutmatimaticas.com.
3. Figuera, J. 2000. Matematik 1: a. Diversifierad. Co-bo-utgåvor.
4. Garcia, m. Numret E i den elementära beräkningen. Återhämtat sig från: matematik.Ciens.Ucv.gå.
5. Wikipedia. Pi -nummer. Återhämtat sig från: Wikipedia.com
6. Wikipedia. Transcendenta nummer. Återhämtat sig från: Wikipedia.com