Notation utvecklade vad som är, exempel och övningar
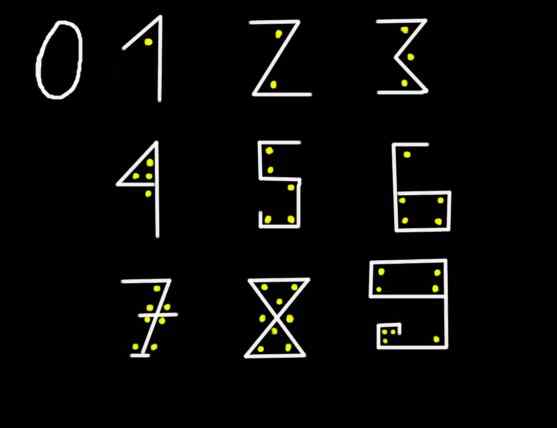
- 1617
- 356
- Anders Larsson
De utvecklad notation Det är en där en numerisk figur uttrycks som en summa där positionsvärdet för varje siffra som bildar antalet beaktas.
Till exempel, när du skriver en siffra som 2345 varje siffra av den har en positionshierarki. Läsning av den högra extrema siffran till vänster, hierarkin eller värdet växer.
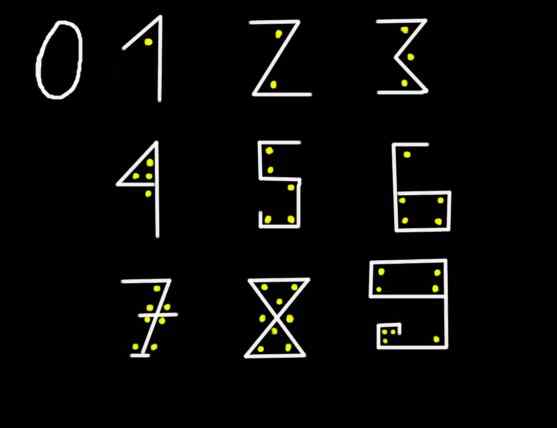 Figur 1. Med nio grafer är det möjligt att representera alla figurer.
Figur 1. Med nio grafer är det möjligt att representera alla figurer. I figur 2345 representerar siffran 5 fem enheter, siffran 4 representerar fyra tiotals, de 3 motsvarar den tredje positionen från vänster till höger och därför representerar de 3 tre hundratals, slutligen de 2 representerar två tusentals. Det vill säga i utvecklad eller utökad notation är figuren 2345 skriven så här:
2345 = 2 tusentals + 3 hundra + 4 tiotals + 5 enheter
Men det kan också uttryckas på följande sätt:
2345 = 2 x 1000 + 3 x 100 + 4 x 10 + 5 x 1.
Figuren 2345 kan också skrivas som summan av krafter på 10:
2345 = 2 x 10^3 + 3 x 10^2 + 4 x 10^1 + 5 x 10^0
Där circumflejo ^ betyder att höja den angivna exponenten. Till exempel 10^3 = 10 x 10 x 10 = 1000. Ett annat sätt att skriva exponenterna är genom en övervakning:
2345 = 2 x 103 + 3 x 102 + 4 x 101 + 5 x 100
[TOC]
Numreringssystem
Det arabiska nummersystemet är siffrorna som används dagligen i de allra flesta kontinenter och länder i världen. Arabiska nummer är ett bassystem 10 eftersom tio symboler eller grafer används för att skriva valfritt nummer. Dessa tio symboler är:
0 1 2 3 4 5 6 7 8 9
Med bara en av dessa symboler kan siffror mellan noll till nio uttryckas. Att uttrycka siffror större än nio, positionssystemet baserat på tio. Figur 10 är ett dussin och noll enheter. Figur 11 är ett dussin och en enhet. Bild 123 (hundra tjugotre) är hundra, två tiotals och tre enheter. Skrivet i form av makter på tio kommer nummer 123 att vara:
Kan tjäna dig: 60 delare1 × 10^2 + 2 × 10^1 + 3 × 10^0
Var:
10^2 = 10 x 10 = 100
10^1 = 10
10^0 = 1.
Med detta exempel är det uppenbart att siffran i slutändan är position 0 och representerar antalet enheter, det för den andra siffran från höger till vänster är position 1 och representerar antalet tiotals, den tredje siffran (rätt till vänster) har position 2 och representerar hundratals.
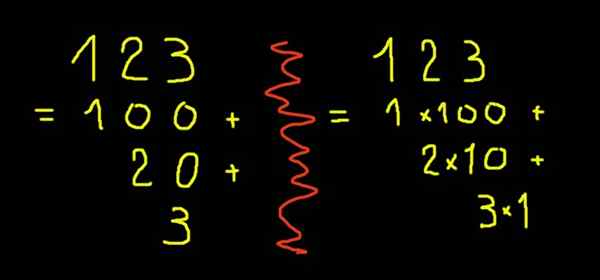 figur 2. Utvecklad notering av figur 123.
figur 2. Utvecklad notering av figur 123. Bråk- eller decimalantal
Med decimalpositionssystemet är det också möjligt.
För att representera fraktionen ½ i det arabiska decimalsystemet, det vill säga hälften av enheten skrivs:
½ = 0,5
För att nå detta uttryck i vårt system baserat på 10 har följande operationer gjorts:
1- Multiplicera teller och nämnar för 5 för att ha motsvarande fraktion 5/10 = 1/2.
2- Dela med 10 motsvarar att multiplicera med kraften baserad på tio med exponent mindre en (10^-1), det vill säga 5/10 = 5 × 10^-1.
3- Den negativa exponenten indikerar hur många gånger den siffra som anges från enhetens position som körs eller placeras, i vårt fall skulle den vara 0,5.
4- ½ = 0,5 I utökad notation är det skrivet så här:
0,5 = 0x10^0 + 5 × 10^-1
Där 10^-1 = 0,1 är en tionde (fraktionen motsvarande enheten uppdelad i 10 lika delar).
På detta sätt motsvarar siffran 0,5 fem tiondelar, men numret 0,05 motsvarar 5 hundratals och 0,005 till 5 tusendelar.
Kan tjäna dig: Varför är algebra viktigt i vissa dagliga livssituationer?Utvecklade noteringsexempel
Exempel 1
Med tanke på 40201 -siffran i standardnotation, konvertera den till den utvecklade notationen.
Lösning:
4 × 10000 + 0x1000 + 2 × 100 + 0x10 + 1 × 1 = 40201
Exempel 2
Skriv fraktionen ¾ i utökad notation.
Lösning:
I det här fallet finns det tre fjärdedelar av enheten.
3/4 = 15/20 = 75/100 = 0,75 = 7/10 + 5/100 =
7 × 10^-1 + 5 × 10^-2.
Sa med ord skulle vara så här:
Fraktionen ¾ motsvarar sju tiondelar plus fem hundratals.
Utvecklade notationsövningar
Övning 1
Säg med ord uttrycket utvecklat av 40201 -figuren i exempel 1.
Lösning:
Den utvecklade notationen är så här:
40201 = 4 × 10000 + 0x1000 + 2 × 100 + 0x10 + 1 × 1
Att på ordspråk sägs det:
Fyra tiotusentals, plus tusentals, plus två hundra, mer noll tiotals, plus en enhet.
Övning 2
Uttrycka med orden föregående figur och bryta ner motsvarande fras utvecklades.
Lösning:
Figuren 40201 i ord uttrycks enligt följande:
Fyrtio tusen två hundra en
Den föregående frasen kan utvecklas som:
40 × 1000 + 2 × 100 + 1
Det kan sägas att sättet att uttala siffrorna är ett halvt utvecklat sätt att uttrycka det.
Övning 3
Skriv på 7/3 utvecklat sätt.
Lösning:
Det är en siffra uttryckt som en felaktig fraktion, eftersom eftersom telleren är större än nämnaren är siffran större än enheten.
Denna felaktiga fraktion kan brytas ned som summan av fraktionerna 6/3 + 1/3. Den första av fraktionerna resulterar i ett helt nummer 2, medan 1/3 = 0,333333, där siffran 3 upprepas på obestämd tid. Så att decimaluttrycket utvecklats av 7/3 -figuren alltid kommer att vara ett ungefärligt uttryck:
Kan tjäna dig: fyrkantig: element, egenskaper, klassificering, exempel7/3 = 2 + 1/3 ≃ 2 + 0,333 = 2 + 3 × 10^-1 + 3 × 10^-2 + 3 × 10^-3.
Övning 6
Skriv i standardnotation och utvecklade sedan numret: Tjugotre miljarder två hundra och femtio miljoner fem hundra tjugo -sex tusen tre hundra tjugo -fem med tre tjugotre tusendelar.
Lösning:
Det bör komma ihåg att a Millardo motsvarar en miljard miljarder. Ordet Millardo Det accepterades av Royal Spanish Academy 1995 på begäran av den sena venezuelanska presidenten Rafael Caldera, en medlem av Venezuelan Academy of Language. I så fall är figuren av standardnotationen skriven enligt följande:
23.2501526.325,023
23 miljarder + 250 miljoner + 526 tusen + 325 enheter + 23 tusendelar.
23 × 10^9 + 250 × 10^6 + 526 × 10^3 + 325 × 10^0 + 23 × 10^-3
Slutligen är figuren i utvecklad notation skriven:
2 × 10^10 + 3 × 10^9 + 2 × 10^8 + 5 × 10^7 + 0x10^6 + 5 × 10^5 + 2 × 10^4 + 6 × 10^3 + 3 × 10^ 2 + 2 × 10^1 + 5 × 10^0 + 0x10^-1 + 2 × 10^-2 + 3 × 10^-3.
Referenser
- Khan akademin. Positionsvärdetabeller. Återhämtad från: är.Khan akademin.org
- Khan akademin. Skriv ett utvecklat nummer (video). Återhämtad från: är.Khan akademin.org
- IFRAH, Geoges (1998): Universal History of Figures. Espasa calpe s.TILL.
- Wikipedia. Positionell notation. Återhämtad från: är.Wikipedia.com
- Wikipedia. Millardo. Återhämtad från: är.Wikipedia.com
- « Fosforoxid (V) struktur, egenskaper, erhållning, användningar, risker
- Aluminiumfosfat (ALPO4) struktur, egenskaper, erhållning, användning »

