Senoidala vågfunktioner, delar, beräkning, exempel

De sinusvågor Det är vågmönster som matematiskt kan beskrivas av sinus- och kosinusfunktionerna. De beskriver med rätta naturliga händelser och variabla tecken i tid, till exempel spänningar som genereras av elektriska växter och används sedan i hem, industrier och gator.

Elektriska element som motstånd, kondensatorer och induktanser, som ansluter till sinusformade spänningsingångar, ger också svar också sinusformade. Matematik som används i deras beskrivning är relativt enkla och har studerats noggrant.

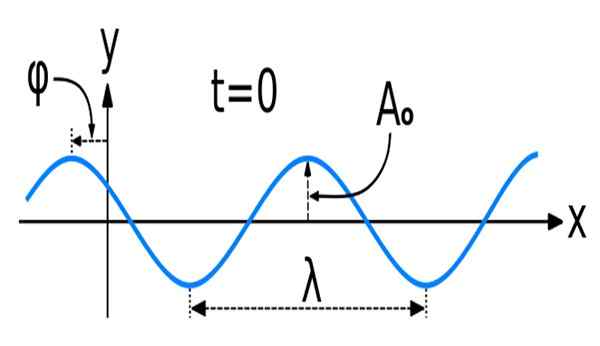
Figur 1. En sinusvåg med några av dess huvudsakliga rumsliga egenskaper: amplitud, våglängd och fas. Källa: Wikimedia Commons. Wave_new_sine.SVG: kraaiennestoriginalt skapad som en kosinusvåg, av användare: pelegs, som fil: wave_new.SVGDERIVATIVE ARBETE: Dave3457 [CC BY-SA 3.0 (https: // CreativeCommons.Org/licenser/BY-SA/3.0)]

Matematiken för sinusformade eller sinusformade vågor, som de också är kända, är den av sinus- och kosinusfunktionerna.

Dessa är repetitiva funktioner, vilket betyder periodicitet. Båda har på samma sätt, med förbehållet att kosinusen förflyttas till vänster med avseende på bröstet i ett cykelrum. Det observeras i figur 2:

figur 2. Sen X- och Cos X -funktioner förflyttas med avseende på den andra. Källa: f. Zapata.

Sedan cos x = sin (x + π/2). Med hjälp av dessa funktioner representeras en sinusvåg. För att göra detta placeras storleken i fråga på den vertikala axeln, medan i den horisontella axeln är tiden belägen.

Den repetitiva kvaliteten på dessa funktioner uppskattas också på ovanstående graf: Mönstret upprepas kontinuerligt och regelbundet. Tack vare dessa funktioner kan du uttrycka spänningar och strömmar i den siniska -typen som varierar med tiden och placerar på den vertikala axeln istället för och, en v eller en Yo att representera spänning eller ström, och på den horisontella axeln istället för x, De t väder.

Det mest allmänna sättet att uttrycka en sinusvåg är:

v (t) = v_m synd (Ωt+φ)

Då kommer vi att fördjupa betydelsen av detta uttryck och definiera några grundläggande termer för att karakterisera sinusvågen.

[TOC]

Fester

Period, amplitud, frekvens, cykel och fas är begrepp som gäller periodiska eller repetitiva vågor och är viktiga för att ordentligt karakterisera dem.

Period

En periodisk funktion som de som nämns, som upprepas med regelbundna intervall, uppfyller alltid följande egenskap:

f (t) = f (t + t) = f (t + 2t) = f (t + 3t) = .. .

Var T Det är ett belopp som heter Vinka, Och det är den tid det tar att upprepa en fas av samma. I internationella systemenheter mäts perioden på några sekunder.

Amplitud

Enligt det allmänna uttrycket för den senoidala vågen v (t) = v_m synd (ωt+φ), v_m Det är det maximala värdet på funktionen, som inträffar när synd (ωt+φ) = 1 (Kom ihåg att det största värdet som sinus- och kosinusfunktionen medger att båda är 1). Detta maximala värde är precis Vågamplitud, också känd som toppamplitud.

Vid en spänning mäts i volt och om det är en ström kommer det att vara i förstärkare. I sinusvågen är bredden konstant, men i andra typer av våg kan amplituden variera.

Kan tjäna dig: Motståndstermometer: Egenskaper, drift, användningar

Cykel

Det är en del av vågen i en period. I den föregående siffran togs perioden genom att mäta den från två på varandra följande toppar eller åsar, men den kan börja mätas från andra delar av vågen, medan de är begränsade av en period.

Notera i följande figur när en cykel täcker från en punkt till en annan med samma värde (höjd) och samma lutning (lutning).

Figur 3. I en sinusvåg sker alltid en cykel under en period. Det viktiga är att utgångspunkten och slutet är i samma höjd. Källa: Boylestad. Introduktion till kretsanalys. Pearson.

Frekvens

Det är mängden cykler som inträffar på 1 sekund och är kopplad till argumentet för sinusfunktionen: ωt. Frekvensen betecknas som F Och det mäts i cykler per sekund eller hertz (Hz) i internationellt system.

Frekvensen är därför periodens omvända mängd:

F = 1/t

Medan frekvensen F är relaterad till Vinkelfrekvens Ω (Pulsation) som:

Ω = 2πF

Vinkelfrekvensen uttrycks i radianer /andra i det internationella systemet, men radianerna är dimensionlösa, alltså frekvensen F och vinkelfrekvens Ω De har samma dimensioner. Observera att produkten ωt ger radianer som ett resultat och måste beaktas när man använder räknaren för att få värdet av Sen ωt.

Fas

Det motsvarar den horisontella förskjutningen som upplever av vågen, med avseende på en tid som tagits som referens.

I följande figur är den gröna vågen avancerad med avseende på det röda i en tid t_d. Två sinusformade vågor är i fas När din frekvens och fas är desamma. Om fasen skiljer sig åt, är de i glipa. Figur 2 Vågor är också föråldrade.

Figur 4. Pelierade sinusidala vågor. Källa: Wikimedia Commons. Ingen maskinläsbar författare tillhandahållen. Kanjo ~ Commonswiki antog (baserat på upphovsrättsanspråk). [Allmängods].

Om vågens frekvens är annorlunda kommer de att vara i fas när fasen ωt+φ vara densamma i båda vågorna på vissa ögonblick.

Senoidvåggenerator

Det finns många sätt att få en sinusformad signal. Hemlagade löpningar ger dem.

Tillämpning av Faradays lag

Ett ganska enkelt sätt att få en sinus signal är att använda Faradays lag. Detta indikerar att i en stängd ström krets, till exempel en slinga, placerad i mitten av ett magnetfält, genereras en inducerad ström när magnetfältet flyter genom det förändras över tid. Följaktligen a Inducerad spänning antingen inducerad FEM.

Magnetfältets flöde varierar om slingan roteras med konstant vinkel snabbhet mitt i fältet skapat mellan polerna N och S för magneten som visas i figuren.

Kan tjäna dig: Neptune (Planet)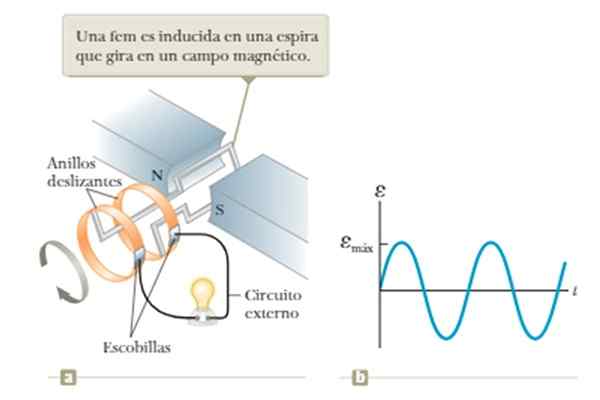Figur 5. Våggenerator baserad på Faradays induktionslag. Källa: Källa: Raymond A. Serway, Jonh W. Jewett [CC BY-SA 4.0 (https: // CreativeCommons.Org/licenser/BY-SA/4.0)].

Begränsningen av denna operativa är beroendet av spänningen som erhålls med frekvensen av rotation av slingan, vilket kommer att ses mer detaljerat i exempel 1 i avsnittet Exempel senare.

Wienoscillator

Ett annat sätt att få en sinusvåg, den här gången med elektron. På detta sätt erhålls sinusvågor vars frekvens och amplitud användaren kan modifiera enligt deras bekvämlighet, med hjälp av växlingsjustering.

Figuren visar en sinus signalgenerator, med vilken andra vågformer också kan erhållas: triangulära och rutor bland andra.

Figur 6. En signalgenerator. Källa: Källa: Wikimedia Commons. Opreg på engelska Wikipedia [CC BY-SA 3.0 (https: // CreativeCommons.Org/licenser/BY-SA/3.0)].

Hur man beräknar sinusvågor?

För att utföra beräkningar som involverar sinusvågor används en vetenskaplig kalkylator som har sinus och kosinus trigonometriska funktioner, liksom dess omvända. Dessa kalkylatorer har lägen för att arbeta vinklarna antingen i grader eller radianer, och det är lätt att konvertera ett sätt till det andra. Omvandlingsfaktorn är:

180 º = π Radianer.

Enligt kalkylatormodellen måste du navigera via lägesnyckeln för att hitta examensalternativet, som gör att du kan arbeta med trigonometriska funktioner i grader, eller radalternativet, för att direkt arbeta vinklarna i radianer.

Till exempel sin 25 º = 0.4226 med räknaren satt i deg -läge. Genom att konvertera 25 º till radianer får du 0.4363 Radianes och Sen 0.4363 rad = 0.425889 ≈ 0.4226.

Oscilloskopet

Oscilloskopet är en apparat som gör det möjligt att visualisera på en skärmtecken på spänningar och strömmar både växla och direkt. Den har knoppar för att justera storleken på signalen på ett rutnät som visas i följande figur:

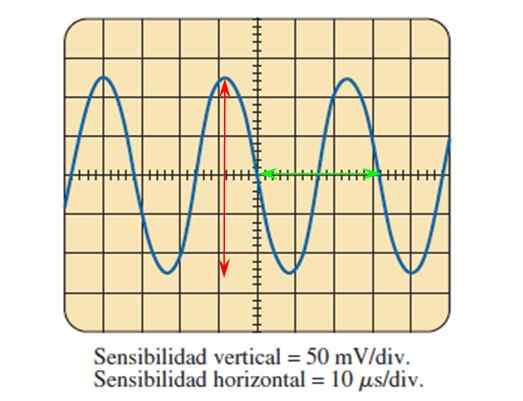Figur 7. En sinusformad signal mätt med ett oscilloskop. Källa: Boylestad.

Genom den bild som tillhandahålls av oscilloskopet och att känna till justeringen av känsligheten i båda axlarna är det möjligt att beräkna vågparametrarna som beskrivs ovan.

Kan tjäna dig: elliptiska galaxer: bildning, egenskaper, typer, exempel

Figuren visar sinusspänningssignalen som en funktion av tiden, där varje uppdelning av den vertikala axeln är värd 50 millivolts, medan i den horisontella axeln är varje division värd 10 mikrosekunder.

Toppen till toppamplituden räknar de uppdelningar som vågen omfattar vertikalt och hjälper till med den röda pilen:

5 divisioner räknas med hjälp av den röda pilen, så topp-pico-spänningen är:

V_pp = 5 divisioner x 50 mV/division = 250 mV.

Pico -spänning V_p Den mäts från den horisontella axeln, är 125 mV.

För att hitta perioden mäts en cykel, till exempel den som avgränsas av den gröna pilen, som täcker 3.2 divisioner, då är perioden:

T = 3.2 divisioner x 10 mikrosekunder/division = 32 mikrosekunder = 32 μs

Exempel

Exempel 1

För generatorn i figur 3, demonstrera från Faradays lag att den inducerade spänningen har sinus. Antag att slingan består av N -svängar istället för en, alla med samma område A och vänder med konstant vinkel snabbhet Ω mitt i ett magnetfält B enhetlig.

Lösning

Faradays lag säger att den inducerade FEM ε är:

ε = -n (dφ_B /dt)

Var Φ_B Det är flödet av magnetfältet, som kommer att vara varierande, eftersom det beror på hur slingan utsätts för fältet varje ögonblick. Det negativa tecknet beskriver helt enkelt det faktum att denna FEM motsätter sig orsaken som producerar den (Lenzs lag). Flödet på grund av en enda slinga är:

Φ_B = B.TILL.cos θ

θ är vinkeln som den normala vektorn till slingans plan bildas med fältet B När rotationen äger rum (se figur) varierar denna vinkel naturligt som:

θ = ωt

Så att: Φ_B = B.TILL.cos θ = b.TILL.cos ωt. Nu måste du bara härleda detta uttryck med avseende på tid och med det erhålls den inducerade FEM:

ε = -n.d (b.TILL.cos ωt) /dt

Som fältet B Det är enhetligt och spasområdet varierar inte, de lämnar derivatet:

ε = -nba. D (cos ωt) /dt = ωnba. Sen ωt

Exempel 2

En slinga har ett område på 0.100 m² och vänd dig till 60.0 varv/s, med sin rotationsaxel vinkelrätt mot ett enhetligt magnetfält på 0.200 t. Att veta att spolen har 1000 varv för att hitta: a) den maximala fem som genereras, b) spolens orientering i förhållande till magnetfältet när den maximala inducerade fem inträffar.

Figur 8. En spiral av N -varv som är trasiga i mitten av ett enhetligt magnetfält och genererar en sinus signal. Källa: R. Serway, Physics for Science and Engineering. Volym 2. Cengage Learning.

Lösning

a) Den maximala FEM är ε_Max = Ωnba

Innan du fortsätter att ersätta värdena måste frekvensen av 60 varv/s till enheter i det internationella systemet skickas. Det är känt att 1 revolution motsvarar en tur eller 2p radianer:

60.0 varv/s = 120p radianer/s

ε_Max = 120p radianer x 1000 varv x 0.200 t x 0.100 m² = 7539.82 V = 7.5 KV

b) När detta värde inträffar Sen ωt = 1 därför:

ωt = θ = 90º,

I detta fall är spiralplanet parallellt med B, så att den normala vektorn till nämnda plan bildas 90º med fältet. Detta inträffar när den svarta vektorn i figur 8 är vinkelrätt mot den gröna vektorn som representerar magnetfältet.

Referenser

1. Boylestad, r. 2011. Introduktion till kretsanalys. 12th. Utgåva. Pearson. 327-376.
2. Figueroa, D. 2005. Elektromagnetism. Fysisk serie för vetenskap och teknik. Volym 6. Redigerad av D. Figueroa. Simon Bolivar University. 115 och 244-245.
3. Figueroa, D. 2006. Fysiklaboratorium 2. Redaktionell equinox. 03-1 och 14-1.
4. Sinusvågor. Återhämtat sig från: iessierradegara.com
5. Serway, R. 2008.Fysik för vetenskap och teknik. Volym 2. Cengage Learning. 881-884