Stationära vågor formler, egenskaper, typer, exempel

De stående vågor De är vågor som sprids i en begränsad hälft, går och kommer in i en del av utrymmet, till skillnad från resande vågor, som när man förökar flyttar bort från källan som har sitt ursprung och inte återvänder till den.

De är grunden för ljuden som produceras i musikinstrumenten, eftersom de lätt uppstår på de fasta strängarna, antingen i ett av dess ändar eller båda. De skapas också i spända membran som trummor eller inuti rör och strukturer som broar och byggnader.

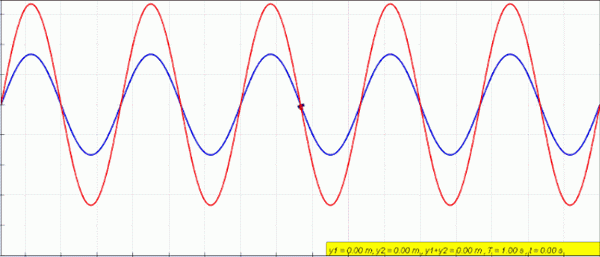Animering av en stationär (röd) våg skapad av superpositionen av en vänster (blå) och höger våg (grön). Källa: LookangMany Tack till författare till Original Simulation = Wolfgang Christian och Francisco Schembre Author of Easy Java Simulation = Francisco Schembre/CC BY-SA (https: // CreativeCommons.Org/licenser/BY-SA/4.0)

När du har ett fast rep i båda ändarna, till exempel en gitarr, skapas vågor med identisk amplitud och frekvens, som reser i motsatta sinnen och kombinerar att producera ett fenomen som heter interferens.

Om vågorna är i fas är åsarna och dalarna inriktade och resulterar i en våg med dubbel amplitud. I så fall talas det om konstruktiv inblandning.

Men om de vågor som stör sig är ur fas, möter ryggarna på en andras dalar och amplituden som är noll. Det är då en destruktiv inblandning.

[TOC]

Formler och ekvationer

Vågens huvudelement för att representera den i rymden och tiden är dess amplitud a, dess våglängd λ och dess vinkelfrekvens ω.

Element i en våg. Källa: Wikimedia Commons.

I matematisk representation är det att föredra att använda k än Vågnummer o Antal gånger vågen per enhet händer. Det är därför det definieras genom längden på λ -vågen som är avståndet mellan två dalar eller två åsar:

K = 2π/ λ

Medan vinkelfrekvens Det är relaterat till perioden eller varaktigheten för en fullständig svängning, till exempel:

Ω = 2π/ t

Och även frekvensen F ges av:

F = ω / 2π

Därför:

F = 1/t

Dessutom rör sig vågorna med hastighet v enligt:

v = λ.F

Matematisk uttryck av den stationära vågen

Matematiskt kan vi uttrycka en våg genom sinusfunktionen eller kosinusfunktionen. Anta att det finns vågor med lika amplitud A, våglängd λ och frekvens ω, spridning längs ett rep och i motsatta sinnen:

och₁ = En synd (kx - ωt)

och₂ = En synd (kx + ωt)

När vi lägger till dem hittar vi den resulterande vågen och_R:

och_R = y₁ + och₂ = En sen (kx - ωt) + en sin (kx + ωt)

Det finns en trigonometrisk identitet för att hitta summan:

Kan tjäna dig: vad är relativt och absolut grovhet?

Sin α + sin β = 2 sin (α + ß)/2 . cos (α - β)/2

Genom denna identitet, den resulterande vågen och_R är kvar:

och_R = [2a Sen Kx] . cos ωt

Plats för noder och magen

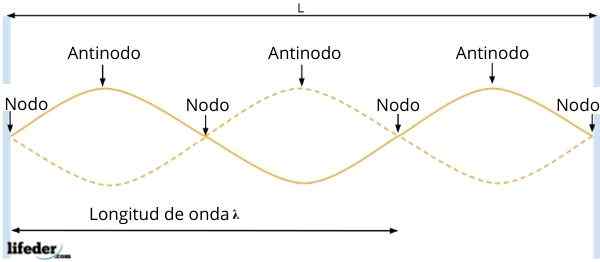Antinodos eller magar och noder

Den resulterande vågen har amplitud till_R = 2ase kx, som beror på partikelns position. Sedan, vid de punkter som Sen Kx = 0, avbryts vågens amplitud, det vill säga det finns ingen vibration.

Dessa punkter är:

Kx = π, 2π, 3π ..

Som k = 2 π/ λ:

(2 π/ λ) x = π, 2π, 3π ..

x = λ/2, λ, 3λ/2 ..

I sådana punkter inträffar förstörande störningar och de kallas knutpunkter. De separeras med ett avstånd lika med λ/2, som härleds från det föregående resultatet.

Och mellan två på varandra följande noder är antinodos eller mage, där vågens amplitud är maximal, eftersom den konstruktiva störningen inträffar. De förekommer när:

Sin Kx = ± 1

Kx = ± π/2, 3π/2, 5π/2 ..

Återigen k = 2 π/ λ och sedan:

x = λ /4, 3λ /4, 5λ /4, ..

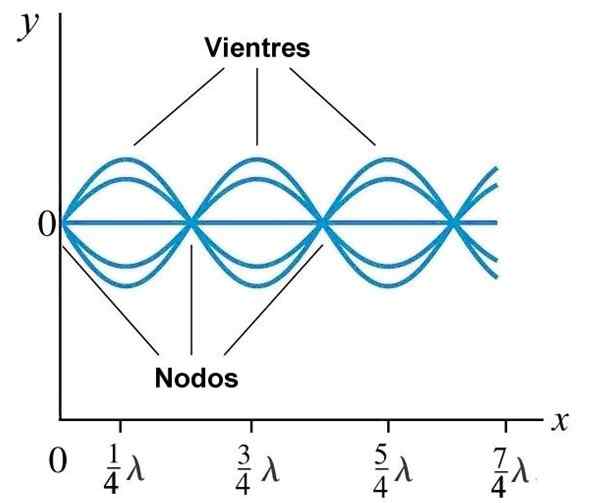Magen eller antinoder och noder i en stationär våg genererad på ett rep med fast ände vid x = 0. Källa: Wikimedia Commons.

Normala lägen på ett rep

Gränsförhållandena på repet avgör hur våglängder och frekvenser är. Om ett rep i längd L är fixerad av dess två ändar, kan den inte vibrera med någon frekvens, eftersom punkterna där repet är fixerade redan är noder.

Dessutom är separationen mellan angränsande noder λ/2, och mellan nod och mage är den λ/4, på detta sätt produceras endast för vissa våglängder stationära vågor: de i vilka en heltal n av λ/2 inuti justeras av de:

(λ/2) = l, med n = 1, 2, 3, 4 .. .

Därför:

λ = 2l/n

Harmoniken

De olika värdena som tas λ kallas harmonik. Således har vi:

-Första harmoniska: λ = 2L

-Andra harmoniska: λ = l

-Tredje harmonik: λ = 2 l/3

-Harmoniskt rum: λ = l/2

Och så vidare.

Hastighet och frekvens

Även om den stationära vågen verkar inte röra sig, är ekvationen fortfarande giltig:

v = λ. F

Därför:

v = (2l/n) . F

F = nv/2l

Nu kan det demonstreras att hastigheten med vilken en våg rör sig i ett rep beror på T -spänningen i samma och dess linjära massadensitet μ (massa per längdenhet) som:

Därför:

Kan tjäna dig: döda laster: egenskaper, beräkning, exempel

Funktioner hos stationära vågor

-När vågorna är stationära sprids den resulterande vågen inte som dess komponenter, som går från en plats till en annan. Det finns punkter där y = 0 eftersom det inte finns någon vibration: noderna, med andra ord, amplituden till_R Det är noll.

-Det matematiska uttrycket av en stationär våg består av produkten av en rumslig del (som beror på X -koordinaten eller rymdkoordinaterna) och en temporär del.

-Bland noderna svänger den resulterande svarta vågen på ett ställe, medan vågorna som går från en plats till en annan är föråldrad där.

-Bara i noderna transporteras inte energi, eftersom detta är proportionellt mot amplitudens kvadrat, men fångas mellan noderna.

-Avståndet mellan angränsande noder är halva våglängden.

-De punkter som repet är fixat betraktas också som noder.

Grabbar

Stationära vågor i en dimension

Vågorna i ett fast rep är exempel på stationära vågor i en dimension, vars matematisk beskrivning vi erbjöd i föregående avsnitt.

Stationära vågor i två och tre dimensioner

Stationära vågor kan också presenteras i två och tre dimensioner, är en något mer komplex matematisk beskrivning.

Racing Ondas Exempel

Fasta strängar

-En sträng fixerad av extrem som oscilleras för hand eller med en kolv av den andra genererar stationära vågor längs dess längd.

Musikinstrument

Stationära vågor skapas i musikinstrument som Violoncello. Källa: Pixabay.

-När du spelar stränginstrument som gitarr, harpa, fiol och piano.

Stlover -vågor skapas också i luftrör, till exempel orgelrör.

Byggnader och broar

Stationära vågor uppstår i strukturer som broar och byggnader. Ett anmärkningsvärt fall var det av Tacoma Narrows Suspension Bridge nära staden Seattle, USA. Strax efter att ha invigdes 1940 kollapsade denna bro på grund av de stationära vågorna som skapades inuti vinden.

Vindfrekvensen matchade med den naturliga frekvensen av bron och skapade i stationära vågor i detta, som ökade deras amplitud tills bron kollapsade. Fenomenet kallas resonans.

Det kan tjäna dig: lätt reflektion

Seichs

I hamnarna finns ett mycket nyfiken fenomen som kallas Seiche, där havets vågor producerar stora svängningar. Detta beror på att vattnet i hamnen är ganska inneslutna, även om det oceaniska vattnet tränger in så ofta genom hamnens ingång.

Port Waters rör sig med sin egen frekvens såväl som havet. Om båda vattnen matchar sina frekvenser finns det en stor stationär våg på grund av resonans, som hände med Tacoma Bridge.

De Seiches De kan också förekomma i sjöar, reservoarer, simbassänger och andra vattendrag begränsade av ytor.

Fisktankar

Stationära vågor kan skapas i en fiskskål som transporteras av en person, om frekvensen med vilken personen är lika med frekvensen för svängen av vattnet.

Träning löst

Gitarrrep har l = 0.9 m och linjär degdensitet μ = 0.005 kg/m. Det utsätts för 72 n spänning och dess vibrationsläge är det som visar figuren, med amplitud 2a = 0.5 cm.

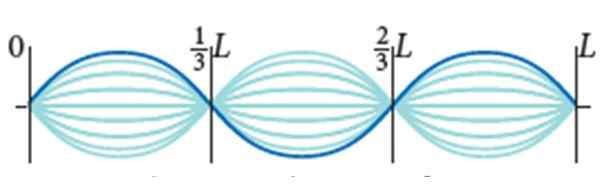Stationära vågor på ett gitarrrep. Källa: Bauer, W. Fysisk.

Hitta:

a) Förökningshastighet

b) vågfrekvens

c) motsvarande stationära vågekvation.

Lösning till

Genom:

Erhålles;

V = [72 n/(0.005 kg/m)]^1/2  = 120 m/s.

Lösning B

Avståndet mellan två angränsande noder är därför λ/2:

(2/3) l - (1/3) l = λ/2

(1/3) l = λ/2

λ = 2l/3 = 2 x 0.90 m / 3 = 0.60 m.

Som v = λ.F

F = (120 m/ s)/ 0.60 m = 200 s^-1= 200 Hz.

Lösning C

Ekvationen är:

och_R = [2a Sen Kx] . cos ωt

Vi måste ersätta värden:

K = 2π/ λ = k = 2π/ 0.60 m = 10 π/3

F = ω / 2π

Ω = 2π x 200 Hz = 400 π Hz.

2A -amplituden ges redan av uttalandet:

2a = 0.5 cm = 5 x 10 ^-3 m.

Därför:

och_R = 5 x 10 ^-3 m . synd [(10π/3) x] . cos (400πt) =

= 0.5 cm . synd [(10π/3) x] . cos (400πt)

Referenser

1. Bauer, w. 2011. Fysik för teknik och vetenskap. Volym 1. MC Graw Hill.
2. Figueroa, D. (2005). Serie: Physics for Science and Engineering. Volym 7. Vågor och kvantfysik. Redigerad av Douglas Figueroa (USB).
3. Giancoli, D.  2006. Fysik: Principer med applikationer. Sjätte. Ed Prentice Hall.
4. Serway, R., Jewett, J. (2008). Fysik för vetenskap och teknik. Volym 1. 7th. Ed. Cengage Learning.
5. Tipler, s. (2006) Fysik för vetenskap och teknik. 5: e upplagan. Volym 1. Redaktör.
6. Wikipedia. Seiche. Återhämtad från: är.Wikipedia.org.