Unidimensionella vågor matematiskt uttryck och exempel

De Ojämnt vågor Det är de som förökas i en riktning oavsett om vibrationer uppstår eller inte i samma förökningsriktning. Ett bra exempel på dem är vågen som rör sig längs ett spänt rep som en gitarr.

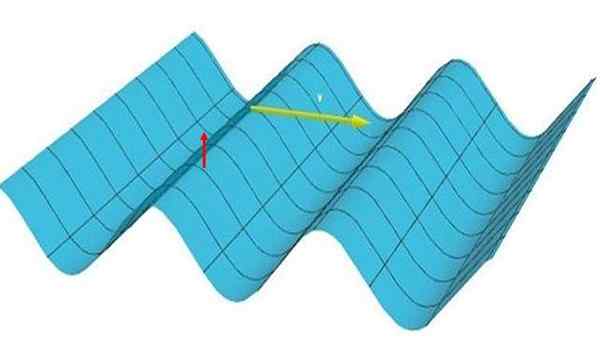
I en platt våg korsa, Partiklarna vibrerar vertikalt (de klättrar och går ner, ser den röda pilen i figur 1), men den är en -dimensionell eftersom störningen reser i en riktning, efter den gula pilen.

Bild 1: Bilden representerar en en -dimensionell våg. Observera att åsar och dalar bildar parallella linjer med varandra och vinkelrätt mot förökningsriktningen. Källa: Självgjord.

Unidimensionella vågor förekommer ganska ofta i vardagen. Följande avsnitt beskriver några exempel på dem och även av vågor som inte är ojämn, för att tydligt fastställa skillnaderna.

[TOC]

Exempel på ojämnvågor och icke -unidimensionella vågor

Ojämnt vågor

Det här är några exempel på en -dimensionella vågor som lätt kan observeras:

- En ljudpuls som reser genom en rak bar, eftersom det är en störning som sprider sig i hela baren.

- En våg som reser genom en vattenkanal, även när förskjutningen av vattenytan inte är parallell med kanalen.

- Vågor som sprids på en yta eller genom det tre dimensionella utrymmet kan också vara en -dimensionell, förutsatt att deras vågfronter är plan parallella med varandra och reser i en riktning.

Icke -dimensionella vågor

Ett exempel på en icke -dimensionell våg finns i vågorna som bildas på en yta av stillvatten när en sten tappas. Det är en tvådimensionell vågfront av cylindrisk våg.

Kan servera dig: spakarmfigur 2. Bilden representerar ett exempel på vad som inte är en en -dimensionell våg. Observera att åsar och dalar bildar cirklar och förökningsriktningen är radiell utåt, det är då en tvådimensionell cirkulär våg. Källa: Pixabay.

Ett annat exempel på icke-facklig dimensionell våg är ljudvågen som genererar en smällare genom explosion på en viss höjd. Detta är en tre -dimensionell våg med sfäriska vågfronter.

Matematisk uttryck av en en -dimensionell våg

Det mest allmänna sättet att uttrycka en en -dimensionell våg som sprider sig utan dämpning i axelens positiva riktning x och med hastighet v Det är matematiskt:

och (x, t) = f (x - v.t)

I detta uttryck och representerar störningen i positionen x Omedelbart t. Vågformen ges av funktionen F. Till exempel är vågfunktionen som visas i figur 1:  och (x, t) = cos (x - v t) och bilden av vågen motsvarar ögonblicket t = 0.

En våg som denna, beskrivet av en kosinus eller sinusfunktion, kallas harmonisk våg. Även om det inte är den enda vågformen som finns, är det av största vikt, eftersom någon annan våg kan representeras som en överlappning eller summa av harmoniska vågor. Det är bekanta Fourier Theorem, så används för att beskriva signaler av alla slag.

När vågen reser i x -axelns negativa riktning förändras den helt enkelt v förbi -v I argument, att vara:

och (x, t) = g (x + v t)

Figur 3 visar animationen av en våg som reser till vänster: det är en form som heter funktion Lorentziana och henne Matematiskt uttryck är:

Kan tjäna dig: arbete: formel, enheter, exempel, övningar

och (x, t) = 1 / (1 + (x + 1⋅t)²

I det här exemplet är förökningshastigheten v = 1, -en enhet av utrymme för varje tidsenhet-.

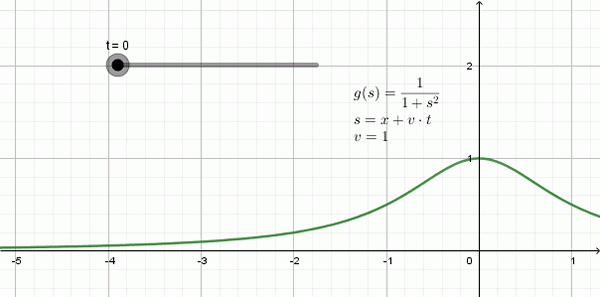Figur 3. Exempel på en Lorentzian -våg som reser till vänster snabbt v = 1. Källa: Utarbetad av F. Zapata med geogebra.

Unidimensional vågekvation

Vågekvationen är en ekvation i partiella derivat, vars lösning naturligtvis är en våg. Det fastställer det matematiska förhållandet mellan den rumsliga delen och dess temporära del och har formen:

Lösningen, som just är funktionen y (x, t), kan verifieras genom ersättning och utveckling i denna ekvation. Till exempel funktioner f (x - v t)  och  G (x + vt)  nämns, de är vågekvationslösningar.

Löst exempel

Då har du det allmänna uttrycket y (x, t) för en harmonisk våg:

och (x, t) = a⋅cos (k⋅x ± Ω⋅t + θo)

a) Beskriv den fysiska betydelsen av parametrarna A, K, ω och θo.

b) vilken mening har tecken ± på kosenos argument?

c) Verifiera att det givna uttrycket verkligen är lösningen på vågekvationen för föregående avsnitt och hitta hastigheten v förökning.

Lösning till)

Vågens funktioner finns i följande parametrar:

-TILL representerar den amplitud eller "våghöjd".

-k är i Vågnummer Och det är relaterat till våglängden λ genom K = 2π/ λ.

-Ω Det är fvinkelutvidgning Och det är relaterat till period T Wave Oscillation av

Ω = 2π/ t.

-θo Det är initialfas, som är relaterat till vågens utgångspunkt.

Kan tjäna dig: statisk friktion: koefficient, exempel, träning

Lösning B)

Negativt tecken tas om vågen reser i den positiva riktningen för x -axeln och det positiva tecknet annars.

Lösning C)

Kontrollera att det givna uttrycket är en lösning på vågekvationen är enkel: det partiella derivatet av funktionen tas och (x, t) När det gäller X två gånger härstammar det delvis från T två gånger och sedan möts båda resultaten för att få jämlikhet:

Andra härrörande från x: ∂²och/ ∂x²= -K². TILL⋅cos (k⋅x ± Ω⋅t + θo)

Andra härrörande från t: ∂²och/ ∂t²= -Ω². TILL⋅cos (k⋅x ± Ω⋅t + θo)

Dessa resultat ersätts i vågekvationen:

 -k². TILL⋅cos (k⋅x ± Ω⋅t + θo) = (1/v²) (-Ω². TILL⋅cos (k⋅x ± Ω⋅t + θo))

Så mycket TILL Eftersom kosinus förenklas, eftersom de visas på båda sidor av jämlikhet och kosinusens argument är detsamma, därför reduceras uttrycket till:

-k² = (1/v²) (-Ω²)

Som gör det möjligt att få en ekvation till v i form av Ω och k:

v² = Ω² / k²

v = ± Ω / k

Referenser

1. E-utbildning. Ekvation av ojämnt harmoniska vågor. Återhämtat sig från: e-kutik.Katedu.är
2. Fysikens rincón. Vågklasser. Hämtad från: fysik.Bloggfläck.com.
3. Figueroa, D. 2006. Vågor och kvantfysik. Serie: Physics for Science and Engineering. Redigerad av Douglas Figueroa. Simon Bolivar University. Caracas Venezuela.
4. Fysiklaboratorium. Vågrörelse. Återhämtat sig från: Fisicalab.com.
5. Peirce, a. Föreläsning 21: The Wase Wave Equation: D'Alemberts lösning. Hämtad från: UBC.Växelström.
6. Vågekvation. Hämtad från: i.Wikipedia.com