Matematik

Beställt par

Beställt par

Vad är ett ordnat par?

Ett ordnat par eller duo Det är en uppsättning av två element som är skrivna enligt den ordning som fastställts av ett visst kriterium. Nämnda kriterier Anger vilka av de två elementen som går först och vilken som går efter.

Det beställda paret betecknas som (x, y), där "x" är det första elementet i paret och "y" är det andra, även kallad Komponenter. I allmänhet (x, y) är det inte samma snygga vridmoment (y, x). Och utöver ordningen är en annan viktig egenskap hos de ordnade paren jämlikhet: två ordnade par (a, b) och (c, d) är desamma endast om a = c och b = d.

Figur 1.- Tack vare de snygga paren vet valpen att benen är begravda på platserna (3,1) och (-4,2), medan hans hus är i (0,0). Källa: f. Zapata.

Exempel på ordnade par skulle vara de som består av ålder och vikten av en matematikstudenter kurs. Det ordnade paret (15, 62) motsvarar en 15 -årig student, annorlunda än det osannolika paret (62,15).

Begreppet ett ordnat vridmoment är mycket viktigt inom olika matematikområden, såsom det kartesiska planet, fraktioner, vektorer i planet, relationer och funktioner. En viktig aspekt är att deras element inte nödvändigtvis har numeriska, till exempel kan de beställas med:

  • Land stad
  • Namn efternamn
  • Fru Man

Och många andra kombinationer.

Exempel på beställda par

Bråk

En fraktion representeras som kvoten på två P/Q -heltal, till exempel fraktionen ½, vilket motsvarar decimalnummer 0.5.

Men denna fraktion är inte den enda som representerar decimalen 0.5, så gör följande:

2/4; 3/6; (-2)/(-4); 20/40; (-1)/(-2) ..

På detta sätt kan alla fraktioner representeras som ett ordnat par (P, Q), där P och Q är hela, med P som ockuperar numratorens position och q den för nämnaren. Det finns en viktig begränsning och att Q (nämnaren) måste vara annorlunda än 0, eftersom fraktionerna i P/0 -formen inte är definierade.

Kan tjäna dig: Finite Set: Egenskaper, exempel, lösta övningar

Och ett annat viktigt tillstånd är att två fraktioner A/B och C/D är lika länge som det uppfylls det:

A ∙ D = B ∙ C

Funktioner och dess grafer

En funktion kan uttryckas som en uppsättning snygga par. Till exempel, genom att grafera en funktion i det kartesiska planet, tilldelas det första elementet positionen för den oberoende variabeln, medan den andra tilldelas den beroende variabeln. Detta är ett ordnat par.

För y = f (x) -funktionen kan det snygga vridmomentet uttryckas som [x, f (x)]]]. Tänk till exempel på startuppsättningen:

A = 1, 2, 3, 4

I denna uppsättning finns det de första komponenterna i ett ordnat par enligt y = x -funktionen2. Uppsättningen av de andra komponenterna är:

B = 1, 4, 9, 16

Och de ordnade paren bildas är:

(1,1); (2,4); (3, 9); (4; 16)

Betrakta.

Vektorer i planet

Vektorer kan representeras i det kartesiska planet genom ordnade par, där det första elementet representerar den horisontella komponenten "X" och den andra den vertikala komponenten "Y". För att skilja vektorerna från punkterna i planet betecknas de med djärva bokstäver och de fyrkantiga konsolerna används istället för parentesen, så här:

v =

Till exempel vektorn v = har en horisontell komponent lika med 4 och vertikal komponent lika med 7. Dess graf är:

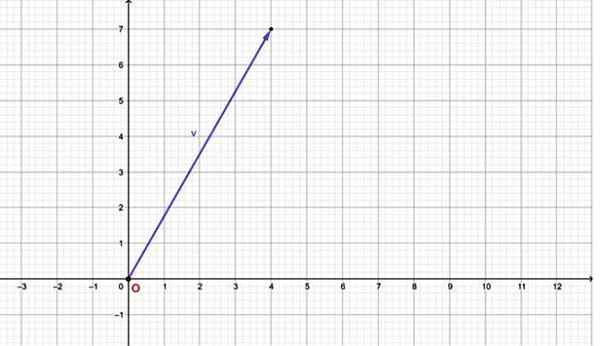figur 2.- En planvektor kan uttryckas genom ett ordnat par. Källa: f. Zapata.

Observera att denna vektor har sitt ursprung sammanfaller med ursprunget till koordinatsystemet (0,0). Om vektorn har sitt ursprung vid någon annan tidpunkt kan det också uttryckas i form av ett ordnat vridmoment genom ett ordnat par, för att göra det på följande avsnitt.

Kan tjäna dig: hierarki av verksamheten

Beställde Pares -verksamheten

Tillägg

Låt målen (a, b) och (c, d) vara par (d). Ett nytt vridmoment erhålls med hjälp av dess summa enligt:

(A, B)+(C, D) = (A+C, B+D)

Neutral element

Det neutrala elementet i tillsatsen av ordnade par är vridmomentet (0,0), eftersom när det lägger till det ordnade paret (a, b) är summan det senare:

(A, B) + (0,0) = (A, B)

Det motsatta summan

Genom att lägga till ett ordnat par (a, b) med sin motsats (-a, -b) erhålls det ordnade vridmomentet (0,0):

(a, b) + (-a, -b) = (0,0)

Kommutativitet

Tilläggsordningen ändrar inte summan:

(A, B) + (C, D) = (C, D) + (A, B)

Associativitet

Resultatet av att lägga till tre ordnade par ändras inte när det grupperas för att utföra operationen:

[(a, b) + (c, d)] + (e, f) = (a, b) + [(c, d) + (e, f)]

Subtraktion av ordnade par

Låt målen (a, b) och (c, d) vara, subtraktionen utförs på följande sätt:

(A, B)-(C, D) = (A-C, B-D)

Produkt

I produkten finns det två alternativ: i) Multiplicera ett vridmoment som beställs med en konstant och ii) Multiplicera två (eller fler) tider.

Multiplikation med en konstant

Låt k vara en konstant och det ordnade vridmomentet (a, b), produkten mellan konstanten och vridmomentet är:

K ∙ (A, B) = (K ∙ A, K ∙ B)

Multiplikation av beställda par

Produkten mellan de beställda paren (a, b) och (c, d) utförs enligt följande:

(A, B) X (C, D) = (AC - BD, BC+AD)

Neutral element

Det neutrala elementet i multiplikation är (1.0), eftersom genom att multiplicera alla vridmoment som beställts av detta, efter regeln om multiplikation som beskrivs ovan, är det ursprungliga vridmomentet:

(A, B) X (1.0) = (A - 0, B + 0) = (A, B)

Kan tjäna dig: Multiplicative Inverse: Förklaring, exempel, lösta övningar

Associativitet

Eftersom faktorernas ordning inte förändrar produkten kan den grupperas på olika sätt att multiplicera tre eller fler snygga par och resultatet är detsamma:

[(a, b) x (c, d)] x (e, f) = (a, b) x [(c, d) x (e, f)]

Löst övningar

Övning 1

Du har beställt par (x2, X-2) = (16, 2). Vilket är värdet på x?

Lösning

Att tillämpa jämlikheten mellan ordnade par erhålls först:

x2 = 16 ⇒ x1 = 4, x2 = -4

För att veta vilka av de två värdena som väljer, användningen av:

X-2 = 2

x = 2 + 2 = 4

Därför är det begärda värdet på X 4.

Övning 2

Uttrycka som ett ordnat par vektorn som går från punkt (1, 3) till punkten (7, 11) och representerar den grafiskt.

Lösning

Vara v Vektorn sökte. För att bestämma det ordnade paret som representerar det och som innehåller dess koordinater subtraheras koordinaterna för ankomstpunkten och ursprungspunkten i den ordningen i den ordningen. Så:

v = =

Vektorn representeras sedan v Som den som går från (1.3) till (7, 11) och utrustningen v vars ursprung är fast vid ursprunget till koordinatsystemet (0,0). Som ni ser har de samma riktning och mening.

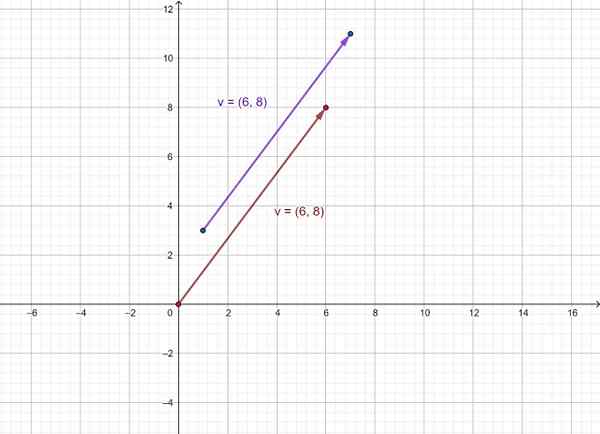Figur 3. Representation av en vektor som ett ordnat par. Källa: f. Zapata.

Referenser

  1. Deepal. Beställt par. Återhämtat sig från: Deepai.org.
  2. Matemovil. Cartesian representation av en vektor av ett ordnat par. Återhämtad från: Matemovil.com.
  3. Varsity tutrorrs. Beställt par. Hämtad från: WarsityTorm.com
  4. Priestri, Juan. Relationer och funktioner. Ingengörsfacilitet. Institutionen för matematik. Buenos Aires 'University. Hämtad från: ämnen.fi.Uba.ar.
  5. University of Denver. Relationer. Återhämtat sig från: matematik.Ucdenver.Edu.