Hydrostatisk tryckformel, beräkning, exempel, övningar

De Hydrostatiskt tryck Det är den som utövar en vätska i statisk jämvikt var som helst inuti, antingen ett område nedsänkt i den, väggarna i behållaren eller en del av vätska som är en del av den totala massan.

Hur vätskor utövar tryck skiljer sig från fasta ämnen. Dessa utövar nedtryck, men en vätska eller en gas gör det i alla riktningar.

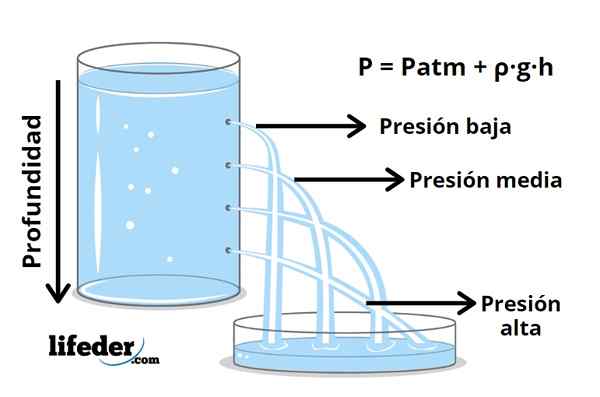
Figur 1- vid större djup större tryck

När det gäller en vätska ökar trycket med djupet, vilket är känt genom erfarenhet när man fördjupar i vattnet där ökningen i trycket känns i öronen. Detta tryck kommer från vätskans vikt och den oavbrutna rörelsen hos partiklarna som komponerar den, som ständigt träffar kroppens yta nedsänkt i vätskan.

Om vi ​​antar en inkomprimerbar vätska - som är sant i de allra flesta applikationer, förblir dess densitet konstant och i så fall beror trycket linjärt på djupet.

[TOC]

Formel

Hydrostatisk tryck beräknas med följande uttryck:

P = p_Bankomat + ρ · g · h

Var:

-P trycket som utövas vid en punkt

-P_Bankomat Det är atmosfärens tryck på den fria ytan

-ρ är flytande densitet

-G är tyngdkraften

-H är det djup som du vill beräkna det hydrostatiska trycket 

Formeln inkluderar effekterna av atmosfären, men många tryck eller manometrar placerar 0 i atmosfärstryck, av detta skäl är det de mäter det differentiella trycket eller det relativa trycket, också kallat mättryck:

P_m = ρ · g · h

När det gäller gaser är de komprimerade eller utvidgas mycket lätt. Därför är dess densitet, som är orsaken mellan massa och volym, vanligtvis en funktion av andra parametrar, såsom höjd och temperatur, i fallet med atmosfäriska gaser.

Det kan tjäna dig: Magnetisering: Orbital och snurrmagnetiskt ögonblick, exempel

Trycket som gaserna utövar kallas vanligtvis aerostatisk tryck, Termen hydrostatiskt tryck för vätskor som reserveras.

Hydrostatiska tryckexempel

Hydrostatisk tryck beror bara på djupet, så formen eller området på behållarens bas är inte relevant.

Eftersom P -trycket definieras som den vinkelräta komponenten i kraften F per enhet A:

P = f/a

Då kan kraften som utövas av vätskan längst ner i en behållare vara annorlunda, men att distribueras över olika tillägg, är trycket, som är kraft/areaförhållandet, detsamma för pekar på samma djup.

Tänk på behållarna med figuren. Trycket är detsamma för alla röda punkter som är på samma nivå, även om det finns en större mängd vätska över den nivån i den centrala behållaren -mer bredd -av vilken det finns det cylindriska och tunna röret i extrema kvar vänster.

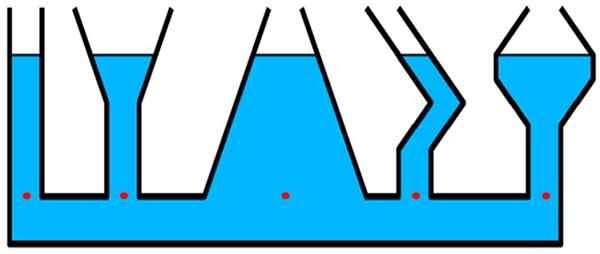figur 2.- Trycket vid någon av de röda punkterna är detsamma, oavsett behållarens form. Källa: Wikimedia Commons.

Strukturer där hydrostatiskt tryck är relevant

-Väggarna i en damm: Även om kraften är densamma för alla punkter i den platta botten, på den vertikala väggen växer den när djupet ökar, så att stödväggarna är bredare i basen än i den övre delen.

-På väggarna och botten av en pool.

-I stjärnor som vår sol, där hydrostatisk tryck balanserar tyngdkraften och håller stjärnan i drift. När den nämnda balansen är trasig, kollapsar stjärnan och lider extrema förändringar i dess struktur.

Kan tjäna dig: vad är det magnetiska ögonblicket?

-Flytande lagringstankar, utformade för att motstå hydrostatiskt tryck. Inte bara väggarna, utan grindarna som underlättar fyllning och extraktion. För sin design beaktas den om vätskan är frätande och även trycket och kraften den utövar enligt dess densitet.

-Däck och ballonger, som är infekterade på ett sådant sätt att de motstår vätsketryck (gas eller vätska) utan att riva.

-Varje nedsänkt kropp, som upplever en vertikal drivkraft, eller "lättnad" av dess vikt, tack vare det hydrostatiska trycket som vätskan utövar. Detta är känt som Archimedes princip.

Övningar

Archimedes -principen bekräftar att genom att sänka en kropp, helt eller delvis, kommer den att uppleva en vertikal kraft uppåt, känd som drivkraft. Styrkans storlek är numeriskt lika med vikten av volymen av vatten som fördrivs av föremålet.

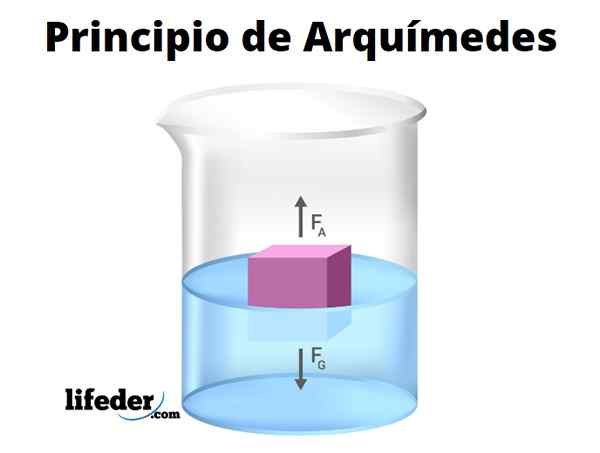
Vara ρ_flytande Vätsketätheten, v_s Den nedsänkta volymen, g Acceleration of Gravity and B THRUST: s storlek, som vi kan beräkna med följande uttryck:

B = ρ_flytande .V_s .g

- Övning 1

Ett rektangulärt block vars dimensioner är 2.0 cm x 2.0 cm x 6.0 cm flottörer i färskt vatten med sin längsta vertikala axel. Längden på blocket som sticker ut över vattnet är 2.0 cm. Beräkna blockdensitet.

Lösning

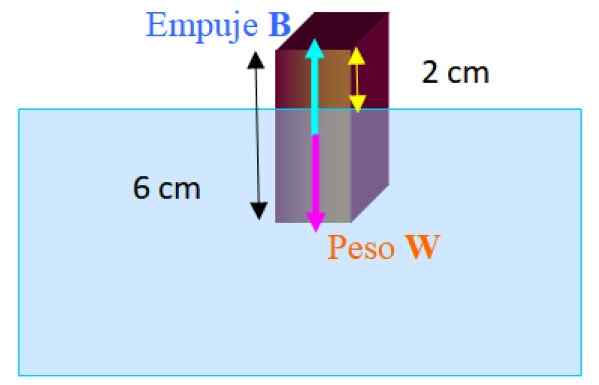Figur 3.- Gratis kroppsdiagram för blocket som flyter delvis nedsänkt i vatten. Källa: f. Zapata.

Krafterna som verkar på blocket är vikten W ner och tryck B uppåt. När blocket flyter i jämvikt har du:

∑ f_och = B - w = 0

B = W

Viktstorleken W är produkten från blockets massa på på grund av tyngdkraften. Vi kommer att använda definitionen av densitet ρ_antingen Som kvoten mellan massan m och volymen V av blocket:

Kan tjäna dig: Mesheal Analys: Begrepp, metoder, exempel

ρ_antingen = M / V → M = ρ_antingen . V

För sin del är drivkraften:

B = ρ_flytande .V_s .g

Utjämna storleken på vikten och storleken på vikten:

ρ_flytande .V_s .G = ρ_antingen . V.g

Tyngdkraften avbryts för att vara som en faktor på båda sidor och blockets densitet kan rensas som:

ρ_antingen = ρ_flytande . (V_s  / V)

Vattentätheten i internationella systemenheter är 1000 kg/m³. Totala V -volymer och nedsänkta V_s, De beräknas med V = bredd x Hög X -djup:

V = 2.0 cm x 2.0 cm x 6.0 cm = 24.0 cm³

V_s = 2.0 cm x 2.0 cm x 4.0 cm = 16.0 cm³

Ersätta värden:

ρ_antingen = ρ_flytande . (V_s  / V) = 1000 kg/ m³ . (16/24) = 667 kg/m³

- Övning 2

Beräkna den nedsänkta volymprocenten av en bit is som flyter i havsvatten till 0 ºC.

Lösning

Is flyter i vatten, eftersom dess densitet är lägre: 916.8 kg/m³, Vilket innebär att det expanderar när det svalnar, till skillnad från de flesta ämnen, att när de värmer upp ökar de sin volym.

Figur 4. Nästan hela volymen av ett isberg förblir nedsänkt. Källa: Pixabay.

Det är en mycket lycklig omständighet för livet, sedan dess fryser massorna av vatten endast på ytan, kvarvarande vätska i djupet.

Havsvattendensiteten är lite större än för färskt vatten: 1027 kg/m³. Vi kommer att beräkna volymfraktionen V_s  / V:

V_s  / V = ​​ρ_antingen / ρ_flytande = 916.8 kg/m³  / 1027 kg/ m³ = 0.8927

Detta innebär att cirka 89 % av isen förblir nedsänkt under vatten. Bara 11 % är synlig flytande vid havet.

Referenser

1. Giambattista, a. 2010. Fysik. 2: a. Ed. McGraw Hill.
2. Riddare, r.  2017. Fysik för forskare och teknik: En strategistrategi. Pearson.
3. Cimbala, c. 2006. Mekanik för vätskor, grundläggande faktorer och applikationer. Mc. Graw Hill.
4. Hibbeler, R. 2015. Flytande mekanik. Första. Ed. Pearson.
5. Mott, r.  2006. Flytande mekanik. 4th. Utgåva. Pearson Education.
6. Gator, v. 1999. Flytande mekanik. McGraw Hill.