Archimedes principformel, demonstration, applikationer

han Archimedes princip Han säger att en helt eller delvis nedsänkt kropp får en vertikal kraft som heter skjuta på, vilket motsvarar vikten av volymen av vätska som förflyttas av kroppen. 

Vissa föremål flyter i vattnet, andra sjunker och andra fördjupar sig själva. För att sjunka en strandboll är det nödvändigt att göra en ansträngning, eftersom den kraften omedelbart uppfattas som försöker återföra den till ytan. Istället sjunker en metallfär. 

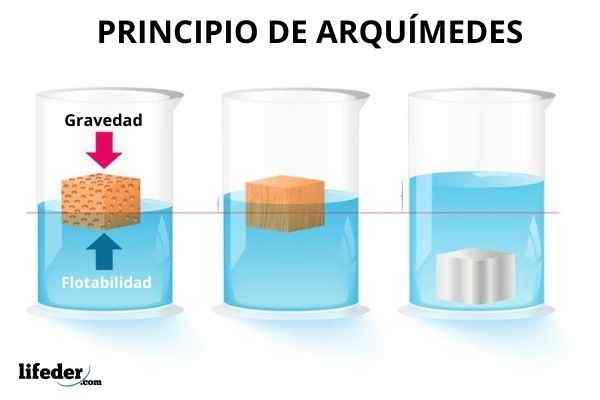
Å andra sidan verkar nedsänkta föremål lättare, därför finns det en kraft som utövas av vätskan som motsätter sig vikt. Men du kan inte alltid kompensera alls till allvar. Och även om det är tydligare med vatten kan gaser också producera denna kraft på de nedsänkta föremålen i dem.

[TOC]

Historia

Archimedes of Syracuse (287-212 a. C.) Det var den som måste ha upptäckt denna princip och var en av historiens största forskare. De säger att kung Hierón II från Syracuse skickade en guldsmed för att tillverka en ny krona, för vilken han överlämnade honom en viss mängd guld.

Archimedes

När kungen fick den nya kronan hade han rätt vikt, men han misstänkte att guldsmeden hade lurat honom genom att lägga till silver istället för guld. Hur kunde jag kontrollera det utan att förstöra kronan?

Hierón kallade Archimedes, vars berömmelse var välkänd, för att hjälpa honom att lösa problemet. Legenden bekräftar att Archimedes var nedsänkt i badkaret när han hittade svaret och, sådant var hans känsla, att han sprang naken genom gatorna i Syracuse för att leta efter kungen skrikande "eureka", vilket betyder "jag hittade det".

https: // giphy.com/gifs/stito3echtlnbvliz3

Vad hittade Archimedes? Tja, när man tar ett badrum vattennivån i badkaret, när han gick in, vilket innebär att en nedsänkt kropp förskjuter en viss vätskevolym.

Och om jag sänkte kronan i vatten, var den också tvungen att flytta en viss vattenvolym om kronan var gjord av guld och en annan om den var gjord av legering med silver.

Archimedes principformel

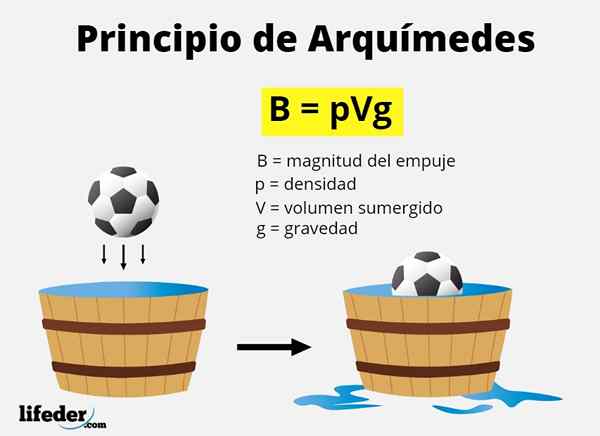
Den reklamstyrka som hänvisas till i Archimedes -principen är känd som skjuta på hydrostatisk antingen flotationskraft Och som vi har sagt motsvarar det vikten av vätskevolymen som förflyttas av kroppen när den är nedsänkt.

Den fördrivna volymen motsvarar volymen på objektet som är nedsänkt, antingen helt eller delvis. Eftersom vikten av något är mg, Och vätskans massa är Densitet x volym, Förneka hur B till storleken på drivkraften, matematiskt det måste:

B = m_flytande x g = fluiddensitet x nedsänkt volym x tyngdkraft

B = ρ_flytande x v_undervattens x g

Där den grekiska bokstaven ρ ("rho") betecknar densiteten.

Den uppenbara vikten

Objektens vikt beräknas av det välkända uttrycket mg, Saker känns dock lättare när de är nedsänkta i vattnet. 

han uppenbar vikt Av ett objekt är det som har när det är nedsänkt i vatten eller annan vätska och att veta det, kan du få volymen på ett oregelbundet föremål som kungen Hieróns krona, som kommer att ses nedan.

Kan tjäna dig: 13 exempel på Newtons första lag i verkliga livet

För att göra detta är det helt nedsänkt i vatten och utsatts för ett rep fäst vid en dynamometer -Ett instrument som förses med en fjäder som tjänar till att mäta krafter-. Ju större vikt på objektet, desto större är töjningen av våren, som mäts på en skala som anges i enheten.

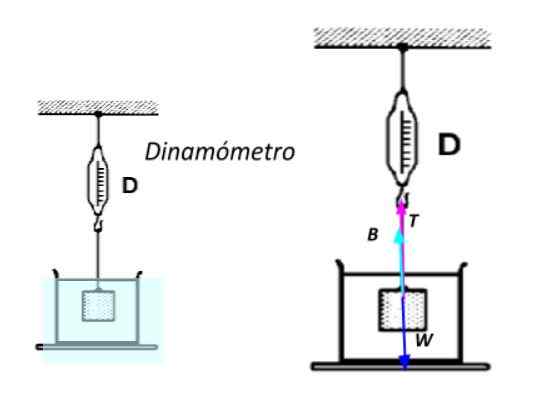Uppenbar vikt av ett nedsänkt objekt. Källa: Utarbetad av F. Zapata.

Tillämpa Newtons andra lag som vet att objektet är i vila:

Σf_och = B + t - w = 0

Den uppenbara vikten w_till Det motsvarar spänningar på t -repet:

T = w_till

W_till = mg - ρ_flytande . V. g

Om den nedsänkta volymen V krävs rensas den som:

V = (w - w_till ) / ρ_flytande  . g

Demonstration

https: // giphy.com/gifs/mcphppgtnpbhl4cgaq

När en kropp fördjupar är drivkraften kraften som härrör från alla krafter som utövas på kroppen genom trycket orsakat av den omgivande vätskan:

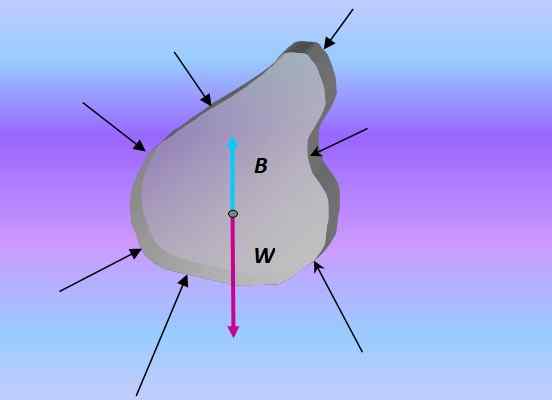Gratis kroppsdiagram över ett nedsänkt objekt. Källa: Utarbetad av F. Zapata.

Tryck och djup

Eftersom trycket ökar med djupet är resultatet av dessa krafter alltid riktat vertikalt uppåt. Därför är Archimedes -principen en följd av det grundläggande teoremet för det hydrostatiska, som relaterar trycket p som utövas av en vätska med djupet z som:

P = ρ.g.z

Krafter på en statisk jämviktsvätska

För att demonstrera Archimedes -principen tas en liten cylindrisk viloparti i vila för att analysera de krafter som utövas på den, som visas i följande figur. Krafterna på cylinderns böjda yta avbryts med varandra. 

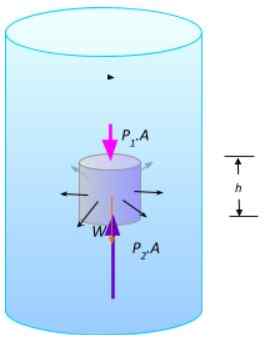En del av vätska i jämvikt. Källa: Utarbetad av F. Zapata.

Storleken på de vertikala krafterna är F₁ = P₁.A och F₂ = P2.A, det finns vikten W. Eftersom vätskan är i balans måste summan av krafterna avbrytas:

∑f_och = P₂.A- p₁.A- w = 0

P₂.A- p₁.A = w

Eftersom drivkraften kompenserar till vikt, eftersom den vätskepartiet är i vila, då:

B = p₂.A- p₁.A = w

Från detta uttryck följer det att drivkraften beror på skillnaden i tryck mellan cylinderns övre ansikte och det nedre. Som W = mg = ρflytande. V. g, Du måste:

B = ρ_flytande. V_undervattens. g

Vilket är just uttrycket för det tryck som nämns i föregående avsnitt.

Archimedes principapplikationer

Ballonger som flyter: Archimedes princip i aktion

Archimedes -principen visas i många praktiska applikationer, bland vilka vi kan namnge:

- Den aerostatiska ballongen. Som genom att ha en genomsnittlig densitet mindre än den omgivande luften, flyter i den på grund av tryckkraften.

- Fartygen. Fartygets hjälm är tyngre än vatten. Men om skrovet betraktas plus luften inuti, är kvoten mellan den totala massan och volymen mindre än vattnet och det är anledningen till att fartygen flyter.

- Livet västar. När de är byggda av lätta och porösa material kan de flyta eftersom massvolymförhållandet är mindre än vatten för vatten.

- Den flytande för att stänga fyllningskiten på en vattentank. Det är en sfär full av stor volymluft som flyter över vattnet, vilket orsakar tryckkraften - multiplicerad med spakeffekten - stänger locket på en vattentank när den har nått nivån totalt.

Det kan tjäna dig: unidimensionella vågor: matematiskt uttryck och exempel

Exempel

Exempel 1

Legenden berättar att kung Hierón gav guldsmeden en viss mängd guld för att göra en krona, men den misstroande monarken trodde att guldsmeden kunde ha lurat när han placerade en mindre värdefull metall i kronan än kronan. Men hur kunde jag veta utan att förstöra kronan? 

Kungen beställde Archimedes och detta, som letade efter lösningen, upptäckte sin berömda princip.

Anta att kronan väger 2,10 kg-F i luften och 1,95 kg-F när den är helt nedsänkt i vatten. I det här fallet finns det inget bedrägeri?

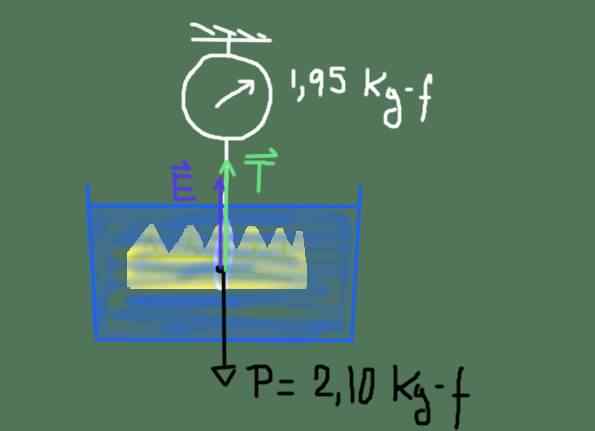King Herons kronfria kroppsdiagram. Källa: Utarbetad av F. Zapata

Kraftsdiagrammet visas i föregående figur. Dessa krafter är: vikten P av kronan, drivkraften OCH och spänningen T av repet som hänger från skalan.

P = 2,10 kg-F och t = 1,95 kg-F är känt, det är nödvändigt att bestämma storleken på drivkraften OCH:

T + e = p ⇒ e = p - t = (2,10 - 1,95) kg -f = 0,15 kg -f

Å andra sidan, enligt Archimedes -principen, motsvarar drivkraften vikten av det utkastade vattnet i den utrymme som ockuperats av kronan, det vill säga tätheten av vattnet genom kronan på grund av accelerationen av tyngdkraften :

E = ρ_vatten⋅V⋅g = 1000 kg/m^3 ⋅ v ⋅ 9,8 m/s^2 = 0,15 kg ⋅ 9,8 m/s^2

Där kronvolymen kan beräknas:

V = 0,15 kg / 1000 kg / m^3 = 0,00015 m^3

Kronens densitet är kvoten mellan kronans massa ur vattnet och volymen på den:

Krondensitet = 2,10 kg / 0,00015 m^3 = 14000 kg / m^3

Densiteten för rent guld kan bestämmas genom en liknande procedur och resultatet är 19300 kg/m^3.

Jämför de två tätheterna är det uppenbart att kronan inte är rent guld! 

Exempel 2 

Baserat på uppgifterna och resultatet av exempel 1 är det möjligt att bestämma hur mycket guld som stulits av guldsmeden i fallet att en del av guldet har ersatts av silver, som har en densitet på 10500 kg/m^3 3.

Vi kommer att kalla ρc till kronans densitet, ρo till tätheten av guld och ρ_p till silverdensiteten.

Kronens totala massa är:

M = ρc⋅v = ρo⋅vo + ρ_p⋅vp

Den totala volymen på kronan är volymen av silver plus volymen av guld:

V = VO + VP ⇒ VP = V - VO

Ersätter i massekvationen:

ρc⋅v = ρo⋅vo + ρ_p⋅ (V - VO) ⇒ (ρo - ρ_p) Vo = (ρc - ρ_pV

Det vill säga att volymen av guld som innehåller kronan på total volym V är:

Vo = v⋅ (ρc - ρ_p)/(ρo - ρ_p) = ..

... = 0,00015 M^3 (14000 - 10500)/(19300 - 10500) = 0,0000596 M^3

För att känna till vikten i guld som innehåller kronan multiplicerar vi VO för gulddensiteten:

Kan tjäna dig: höger handregel

MO = 19300 *0,00005966 = 1,1514 kg

Eftersom kronans massa är 2,10 kg, vet vi att 0,94858 kg guld blev stulen av guldsmeden och ersattes av silver.

Löst övningar

Övning 1

En enorm heliumballong kan upprätthålla i balans (utan att gå upp eller gå ner) till en person.

Antag att personens vikt, plus korgen, strängarna och ballongen är 70 kg. Vad är volymen av helium som krävs för att detta ska hända? Vilken storlek kommer ballongen att ha?

Lösning

Vi antar att drivkraften produceras huvudsakligen av heliumvolymen och att drivkraften för resten av komponenterna är mycket liten jämfört med den för helium som upptar mycket mer volym.

I detta fall krävs en heliumvolym som kan tillhandahålla en 70 kg + vikttryck.

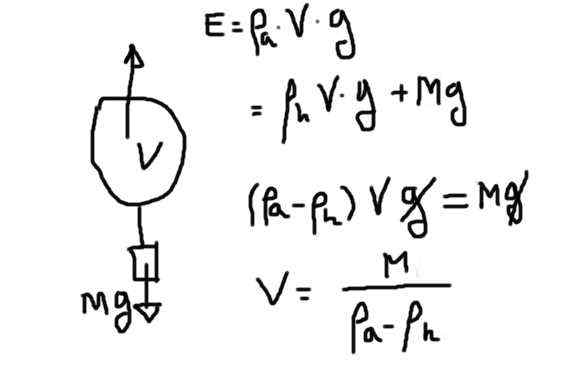Gratis kropp fdiaogram full av helium. Källa: Utarbetad av F. Zapata.

Trycket är produkten från heliumvolymen på grund av heliumens densitet på grund av tyngdkraften. Den drivkraften måste kompensera för heliumens vikt plus resten av resten.

Da⋅v⋅g = da⋅v⋅g + m⋅g

Där det drar slutsatsen att v = m / (da - dh)

V = 70 kg / (1.25 - 0,18) kg/m^3 = 65.4 m^3

Det vill säga 65 krävs.4 m^3 av helium vid atmosfärstryck för stöd.

Om vi ​​antar en sfärisk ballong kan vi hitta radien för densamma från förhållandet mellan volymen och en sfärs radie:

V = (4/3) ⋅π⋅r^3

Där r = 2,49 m. Med andra ord krävs en 5 m diameter full av helium.

Övning 2

Material med lägre densitet som vatten flyter i samma. Antag att du har polystyrenbitar (vit kork), trä och is. Hans täthet i kg per kubikmeter är respektive: 20, 450 och 915.

Hitta vilken fraktion av den totala volymen är ur vattnet och vilken höjd som sticker ut med avseende på ytan på vattnet som tar som densitet på de senare 1000 kg per kubikmeter.

Lösning 

Flytbarhet inträffar när kroppsvikten är lika med drivkraften på grund av vatten:

E = m⋅g

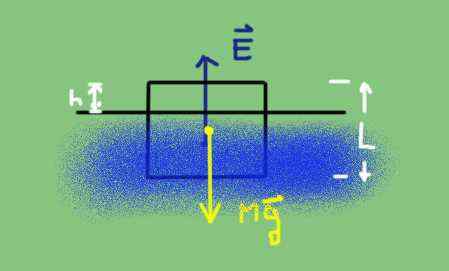Gratis kroppsdiagram över ett delvis nedsänkt objekt. Källa: Utarbetad av F. Zapata.

Vikt är kroppstätheten DC multiplicerad med sin volym V och genom accelerationen av tyngdkraften g.

Ansträngningen är vikten av den fördrivna vätskan enligt Archimedes -principen och beräknas genom att multiplicera vattens densitet D med den nedsänkta volymen V 'och genom tyngdkraften.

Det är:

D⋅v'⋅g = dc⋅v⋅g

Vilket innebär att den nedsänkta volymfraktionen är lika med kvoten mellan kroppstäthet och vattentäthet.

(V '/V) = (DC/D) 

Det vill säga att den enastående volymfraktionen (V "/V) är

(V "/V) = 1 - (DC/D)

Ja h Det är den enastående höjden och L Kubsidan Volymfraktionen kan skrivas som

(H⋅l^2)/(l^3) = h/l, Med andra ord är den enastående höjdfraktionen också

(H/L) = 1 - (DC/D)

Då är resultaten för de begärda materialen:

Polystyren (vit kork):

(H/L) = (V "/V) = 1 - (DC/D) = 1- (20/1000) = 98% Ur vattnet

Trä:

(H/L) = (V "/V) = 1 - (DC/D) = 1- (450/1000) = 55% Ur vattnet

Is:

(H/L) = (V "/V) = 1 - (DC/D) = 1- (915/1000) = 8.5% Ur vattnet

Referenser

1. Bauer, w. 2011. Fysik för teknik och vetenskap. Volym 1. MC Graw Hill. 417-455.
2. Cengel Y, Cimbala J. 2011.Flytande mekanik. Grundläggande faktorer och ansökningar. Första upplagan. McGraw Hill.
3. Figueroa, D. (2005). Serie: Physics for Science and Engineering. Volym 4. Vätskor och termodynamik. Redigerad av Douglas Figueroa (USB). 1 - 42.
4. Giles, r. 2010. Flytande och hydraulisk mekanik. McGraw Hill. 
5. Rex, a. 2011. Fysikens grunder. Pearson. 239-263.
6. Tippens, s. 2011. Fysik: koncept och applikationer. Sjunde upplagan. McGraw Hill.