Fysisk

Princip om kraftöverförbarhet

Princip om kraftöverförbarhet

Vi förklarar vad som är principen om överförbarhet, med exempel och övningar löst

Vad är överförbarhetsprincipen?

han Överförbarhetsprincip Det gäller för fasta föremål och bekräftar att en applicerad kraft på någon punkt i kroppen motsvarar en annan kraft med lika stor storlek och riktning, så länge som den nämnda kraften appliceras på samma linje som innehåller den ursprungliga kraften.

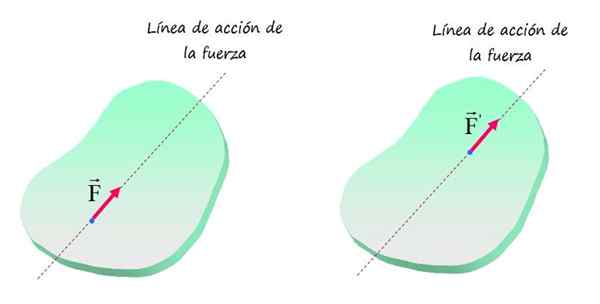
Därför kommer varje kraft med samma storlek och riktning att orsaka samma effekt av translationell och rotationsrörelse på objektet, förutsatt att dess tillämpningspunkt är belägen på samma linje, som visas i följande figur.

I en styv kropp modifieras inte effekten av en kraft när appliceringspunkten för den rör sig längs dess handlingslinje. Källa: f. Zapata.

Krafterna som visas F och F'Det sägs att de är det motsvarande krafter och den plötsliga raka linjen som innehåller dem kallas tvinga handlingslinje.

Transmissibility -principen är mycket användbar, eftersom den gör det möjligt att bekväma de krafter som verkar på objektet för att underlätta analysen.

Förklaring av Överförbarhetsprincip

Överförbarhetsprincipen är baserad på det faktum att två krafter F1 och F2 De är likvärdiga, under förutsättning att de har samma storlek och samma riktning.

Dessutom måste de producera samma ögonblick med avseende på vilken punkt som helst eller, vilket garanteras genom att ha samma handlingslinje och eftersom ögonblicket är produkten av kraft på avståndet till eller till nämnda linje.

Observera att principen endast gäller på en styv kropp, det vill säga ett objekt där de relativa avstånden mellan deras delar inte förändras, eftersom de inre krafterna som håller den i sammanhållning är tillräckligt intensiva. Därför modifierar objektet inte sin form, vare sig de externa krafterna verkar på det eller inte.

Å andra sidan, om objektet inte är styvt, skulle modifiering av tillämpningspunkten för krafterna ge variationer i termer av spänning eller kompression som tillämpas på kroppen, vilket skulle leda till förändringar i dess form.

Antag naturligtvis att en kropp är styv är inget annat än en idealisering, eftersom alla föremål i verkligheten är deformerbara i större eller mindre utsträckning. Men i många fall är det ett utmärkt tillvägagångssätt, om deformationen är tillräckligt liten för att betraktas som föraktligt.

Begränsningar

Transmissibility -principen har, som anges, en begränsning beträffande de interna effekterna av skjutning eller skjutning av krafterna. I följande figur visas ett objekt, med krafterna F och F'Tillämpas i olika punkter av samma handlingslinje.

Kan tjäna dig: Archimedes Princip: Formel, Demonstration, Applications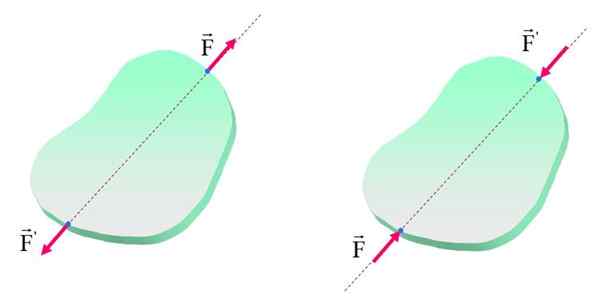Transmissibilitetsprincipen är endast tillämplig i styva kroppar, eftersom modifiering av tillämpningspunkten för krafterna kan orsaka olika effekter på deformerbara kroppar. Källa: f. Zapata.

Observera att i båda figurerna är kroppen (styv eller inte) i balans, eftersom krafterna har lika stor storlek och riktning och motsatta sinnen. Dessutom är krafterna, som har sagts, på samma handlingslinje, men i den vänstra figuren är effekten på kroppen spänning medan till höger är effekten komprimering.

Därför, även om kroppen förblir i vila, är de interna effekterna olika och blir patent om objektet inte är helt styvt. När det gäller vänstern tenderar krafterna att förlänga kroppen, medan de till höger tenderar att förkorta den.

Exempel på Överförbarhetsprincip

Exempel 1

Anta att du har en tung bagageutrymme på ett horisontellt golv. Effekten av att trycka den på vänster sida är densamma som om den är platt. I det här fallet är stammens rörelse på marken densamma.

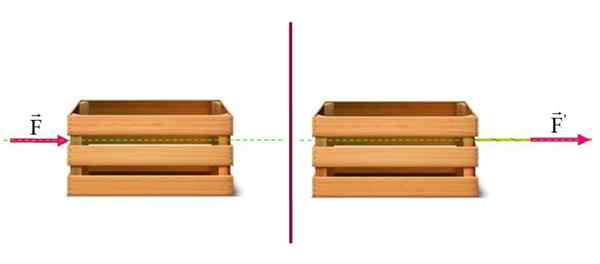Effekten av att trycka eller dra lådan på den horisontella ytan är densamma: flytta den från vänster till höger. Källa: f. Zapata.

Exempel 2

Du har en lång plank som en hylla. För att installera det är det motsvarande.

I båda fallen kommer krafterna som balanserar planken att ha samma storlek och riktning, som verkar på samma handlingslinjer, men tillämpas på olika punkter.

Överförbarhetsprincipen och ögonblicken

Anta att det finns en kraft F som appliceras vid en punkt A, det ögonblick som härstammar denna kraft runt punkten eller visas i figuren är:

MANTINGEN = rTILL × F

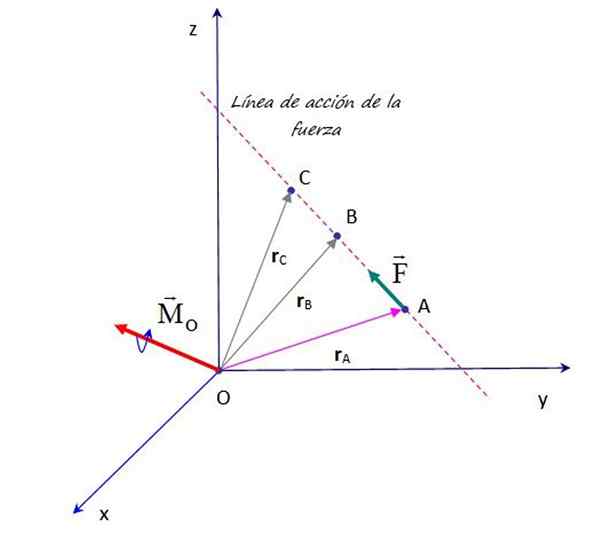Glida eller överföra kraft längs sin handlingslinje modifierar inte det ögonblick det utövar på punkten eller. Källa: f. Zapata.

Tja, överförbarhetsprincipen säkerställer det F, Att agera på vilken punkt som helst längs sin handlingslinje, till exempel punkter B, C och mer, har sitt ursprung samma ögonblick med avseende på punkten eller. Därför är det giltigt att bekräfta att:

MANTINGEN = rTILL × F  = rB × F = rC × F

Löst övningar

Övning 1

En homogen sfär har massa m = 5 kg och vilar på en horisontell yta utan friktion.

    • a) Rita in ett schema som kraften som utövas av ytan på sfären.
    • b) Bygg sfärens fria kroppsdiagram
    • c) Beräkna värdet på den normala kraften som utövas av ytan på sfären.

  • Lösningar A och B

I graf a) Kraften som utövas av ytan på sfären visas, kallas normal N, Eftersom det är vinkelrätt mot ytan. Punkten för tillämpningen av kraften sammanfaller med sfärens stödpunkt på ytan (punkt i grönt) och handlingslinjen är den vertikala som passerar genom sfärens geometriska centrum.

Kan tjäna dig: Jordens magnetosfär: Egenskaper, struktur, gaser

I graf B) finns det fria kroppsdiagrammet över sfären, där bortsett från den normala visas vikten, som appliceras i tyngdpunkten, betecknad med den gula punkten.

Tack vare överföringsprincipen, normal kraft N Det kan överföras till denna punkt utan att ändra effekterna på sfären. Dessa effekter är inte andra som håller sfären som stöds på bordet i balans.

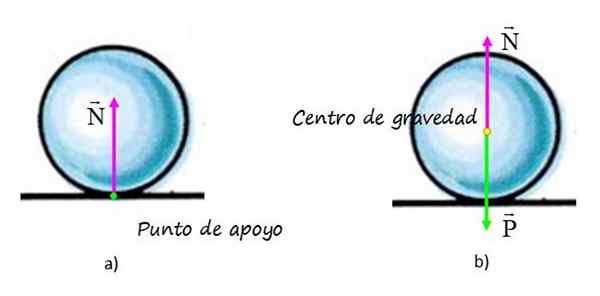I figur A) till vänster, de normala handlingarna på sfärens stödpunkt med ytan. I figur B), på det fria kroppsdiagret överförs normalt till tyngdpunkten, eftersom vertikalen är dess handlingslinje. Dess effekter är inte modifierade, eftersom den balanserar vikten så att sfären är i balans. Källa: f. Zapata.

  • Lösning C

Eftersom sfären är i balans, tar det som en positiv mening den vertikala upp och negativa den vertikala ner, resulterar Newtons andra lag i:

N - p = 0

Det vill säga vikten och normalen är balanserade, därför är de desamma i storlek:

N = p = mg = 5 kg × 9.8 m/s2 = 49 n, riktad vertikalt upp.

Övning 2

Ange om i följande fall är överföringsprincipen uppfyllt:

  • Första fall

En kraft på 20 n horisontellt applicerad på en styv kropp ersätts av en annan kraft på 15 n applicerad vid en annan punkt på kroppen, även om båda gäller i samma riktning.

    • Lösning

I detta fall kommer överförbarhetsprincipen inte att uppfyllas eftersom även om de två krafterna gäller i samma riktning har den andra kraften inte samma storlek som den första. Därför ges ett av de oumbärliga villkoren i överförbarhetsprincipen.

  • Andra fall

En kraft på 20 N horisontellt applicerad på en styv kropp ersätts av en annan av 20 N, appliceras vid en annan punkt i kroppen och vertikalt.

    • Lösning
Kan tjäna dig: Planck Constant: Formler, värden och övningar

Vid detta tillfälle uppfylls inte överföringsprincipen eftersom även om de två krafterna har samma modul, gäller de inte i samma riktning. Återigen ges ett av de oumbärliga villkoren i principen om överförbarhet inte. Det kan sägas att de två styrkorna är likvärdiga.

  • Tredje fall

En kraft på 10 n ändras horisontellt på en styv kropp tillämpas också på en annan punkt i kroppen, men på samma riktning och mening.

    • Lösning

I detta fall uppfylls överföringsprincipen, eftersom de två krafterna är av samma storlek och tillämpas i samma riktning och betydelse. Alla nödvändiga villkor för överförbarhetsprincipen är uppfyllda. Det kan sägas att de två styrkorna är likvärdiga.

  • Fjärde fallet

En kraft är glider i riktning mot din handlingslinje.

    • Lösning

I det här fallet uppfylls överförbarhetsprincipen eftersom den samma kraften, som den tillämpade kraften, är samma kraft, varierar inte och den glider in i dess handlingslinje. Återigen uppfylls alla nödvändiga villkor för överföringsprincipen.

Övning 3

På en styv kropp gäller två yttre krafter. De två krafterna gäller i samma riktning och i samma riktning. Om den första modulen är 15 n och den för den andra av 25 n, vilka förhållanden bör en tredje extern kraft som ersätter resulterande från de två föregående för att möta överföringsprincipen?

  • Lösning

Å ena sidan måste värdet på den resulterande kraften vara 40 N, vilket är resultatet av att lägga till modulen för de två krafterna.

Å andra sidan måste den resulterande kraften agera var som helst i den raka linjen som ansluter sig till de två tillämpningspunkterna för de två krafterna.

Referenser

  1. Bedford, 2000. TILL. Mekanik för teknik: statisk. Addison Wesley. 
  2. Öl, f. 2010. Vektormekanik för ingenjörer. McGraw Hill. Femte. Utgåva.
  3. Giancoli, D.  2006. Fysik: Principer med applikationer. Sjätte. Ed Prentice Hall.
  4. Hibbeler, R. 2004. Ingenjörsmekanik: statistik. Prentice hall.
  5. Meriam, j.L. 2012. Ingenjörsmekanik: statistik. Sjunde upplagan. Wiley & Sons.