Pentagonal prismegenskaper, delar, vertikaler, kanter, volym

En Pentagonal prismat Det är en tre -dimensionell geometrisk figur vars baser, identiska, har en Pentagon -form och har också totalt 5 -sidor i form av parallellogram.

Om ansikten är rektangulära sägs det att det är en Rak femkantig prisma, Även om kanterna är benägna till baserna, är det en sned pentagonal prismat. I följande bild finns det ett exempel på var och en.

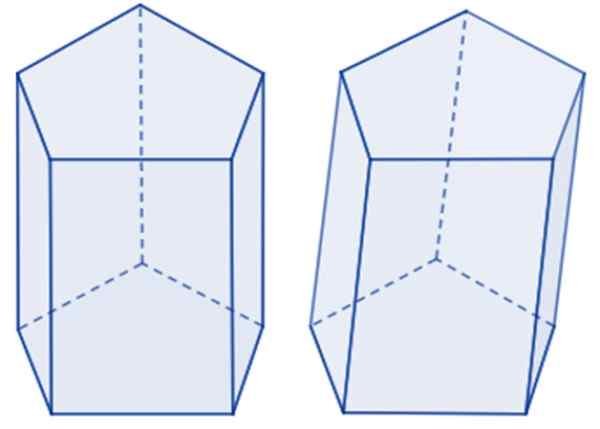Pentagonal prisma till vänster och sned till höger. Källa: Wikimedia Commons.

Basen Pentagon kan vara regelbunden om dess fem sidor har samma mått, liksom inre vinklar, annars är det en oregelbunden Pentagon. Om prisma basen är regelbunden handlar det om Regelbundet Pentagonal Prism. Annars är ett prisma oregelbunden femkantig.

Oregelbundna pentagonala prismor som används i modern konstruktion. Källa: tapet flare.

Pentagonal Prism är en harmonisk struktur som används i arkitektur och design av föremål, till exempel den moderna byggnaden som visas i den övre figuren. Oregelbundna Pentagons formade fönster utgör prismans bas.

[TOC]

Pentagonal prismegenskaper

-Det är en tre -dimensionell geometrisk figur, ytorna som komponerar den innehåller en viss volym.

-Deras baser är pentagoner och deras sidos ansikten kan vara rektanglar eller parallellogram.

-Den har vertikaler -hörnen på prisma -och kanter -bords eller stränder-.

-Om kanterna som förenar baserna är vinkelräta mot dem, är prismen rak, och om de är benägna är prisma snedställda.

-När basen är en Pentagon vars inre vinklar är mindre än 180º är prismen konvex, Men om en eller flera inre vinklar är större än 180º är det ett prisma konkav.

Pentagonal Prism Elements

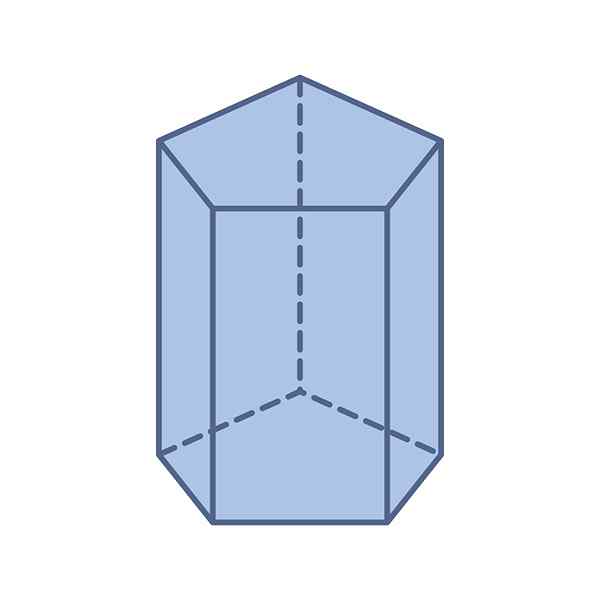
-Baser: Den har två femkantiga och kongruenta baser -deras mätningar är desamma -varken regelbundna eller oregelbundna.

Kan tjäna dig: Allmän formel: Kvadratiska ekvationer, exempel, övningar

-Inslag: Ett femkantigt prisma har totalt sju ansikten: de två femkantiga baserna och de fem parallellogrammen som utgör sidorna.

-Kant: segment som förenar två baser, som visas i rött i figur 3 eller den som går med två sidor.

-Höjd: Avstånd mellan ansikten. Om prismen är rak sammanfaller detta avstånd med kanten på kanten.

-Vertex: Vanlig punkt mellan en bas och två sidosidor.

Den nedre figuren visar ett regelbundet Pentagonal Prisma, där de segment som bildar basen har lika mått, kallad till.

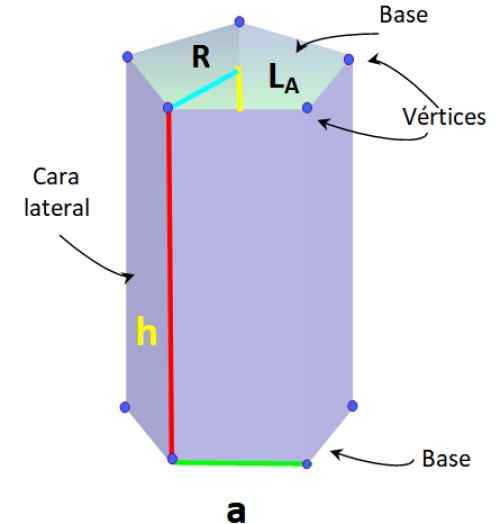 Regelbundna pentagonala prisma element. Källa: f. Zapata.

Denna typ av prisma har också följande element, typiska för den vanliga Pentagon:

-Radio R: Avstånd mellan centrum av Pentagon och en av vertikalerna.

-Apothem l_TILL: segment som går med i mitten med mittpunkten till en av sidorna av Pentagon.

Hur många vertiklar har ett femkantigt prisma?

I en Pentagon finns det 5 vertikaler och eftersom det femkantiga prismen har två pentagoner som baser, har denna kropp totalt 10 vertikaler.

Hur många kanter har ett femkantigt prisma?

Du kan beräkna antalet kanter för geometriska kroppar med platta ansikten, till exempel prismor, med hjälp av Euler teorem För konvexa polyhedros. Leonhard Euler (1707-1783) är en av de största matematikerna och fysiska i historien.

Satsen skapar en relation mellan antalet ansikten, som vi kommer att kalla C, mängden vertikaler V och de totala kanterna a enligt följande:

C+V = A+2

För det femkantiga prismen har vi: C = 7 och V = 10. Clearing till, antalet kanter:

Det kan tjäna dig: Bijjektiv funktion: Vad är det, hur görs det, exempel, övningar

A = C+V-2

Ersätta värden:

A = 7 + 10 - 2 = 15

Ett femkantigt prisma har 15 kanter.

Hur man får volymen av ett femkantigt prisma?

Volymen på det femkantiga prismen mäter utrymmet som låsts av sidorna och baserna. Det är ett positivt belopp som beräknas av följande egenskap:

Varje plan som skär till prisma vinkelrätt mot dess kanter, genererar en korsning på samma sätt som basen, det vill säga en Pentagon av samma dimensioner.

Därför är volymen av det femkantiga prismen produkten från basområdet och prisets höjd.

Vara TILL_B det femkantiga basområdet och h Prismets höjd, sedan volymen V är:

V = a_B x h

Denna formel är allmän och är giltig för alla prisma, antingen regelbundna eller oregelbundna, raka eller sned.

Volymen på ett prisma finns alltid i enheter med längd högt till kuben. Om längden på sidorna och prisets höjd ges i meter, uttrycks volymen i M³, att "kubikmeter" läses. Andra enheter inkluderar CM³, km³, tum³ och mer.

- Regelbunden pentagonal prismvolym

I Pentagonal Prism regelbundet är baserna vanliga pentagoner, vilket innebär att sidan och inre vinklar är desamma. Med tanke på kroppens symmetri beräknas Pentagon -området och därför volymen på flera sätt:

Att känna till höjden och mätningen av sidan

Vara till Måttet på den femkantiga bassidan. I så fall beräknas området av:

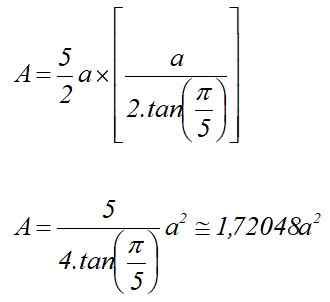
Därför är volymen på det vanliga femkantiga prismen på höjd h:

Kan tjäna dig: imaginära nummer: egenskaper, applikationer, exempel

V = 1.72048 a²⋅ H

Att känna till radens höjd och mått

När Radio R Från den femkantiga basen kan denna andra ekvation användas för basområdet:

A = (5/2) r²⋅ SEN 72º

På detta sätt ges volymen av det femkantiga prismen av:

V = (5/2) r² ⋅ H ⋅ SEN 72º

Var h Det är prisets höjd

Att känna till höjden, måttet på apotem och omkretsvärde

Det femkantiga basområdet kan beräknas om dess omkrets P är känd, vilket helt enkelt är summan av sidorna, liksom måtten på apotem l l l_TILL:

A = p. L_TILL / 2

Multiplicera detta uttryck med värdet på höjd h, Vi har priset av prisma:

V = P. L_TILL .H / 2

- Oregelbunden pentagonal prismvolym

Formeln som ges i början är till och med giltig när priset är en oregelbunden Pentagon:

V = a_B x h

För att beräkna basområdet används till exempel olika metoder: till exempel:

-Trianguleringsmetod, som består av att dela upp pentagon i trianglar och fyrkantiga, vars respektive områden lätt beräknas. Pentagon -området kommer att vara summan av områdena i dessa enklare siffror.

-Gauss Determinants Method, för vilken du måste känna till figuren i figuren.

När värdet på området har fastställts multipliceras det med prisets höjd för att få volymen.

Referenser

1. Alexander, D. 2013. Geometri. Femte. Utgåva. Cengage Learning.
2. Matematik öppen referens. Polygonområde. Återhämtat sig från: MathPenref.com.
3. Universumsformler. Euler teorem för polyhedros. Återhämtat sig från: universalformulor.com.
4. Universumsformler. Område med en vanlig Pentagon. Återhämtat sig från: universalformulor.com.
5. Wikipedia. Prisma. Återhämtad från: är.Wikipedia.com.
6. Wikipedia. Pentagonal prismat. Återhämtad från: är.Wikipedia.com.