Frekvens sannolikhetskoncept, hur beräknas och exempel

De Frekvenssannolikhet är en underdefinition inom studien av sannolikhet och dess fenomen. Dess studiemetod med avseende på händelser och attribut är baserad på stora mängder av iterationer, och därmed observerar var och en på lång sikt eller till och med oändliga repetitioner.

Till exempel innehåller ett gummitan -kuvert 5 gummi i varje färg: blått, rött, grönt och gult. Du vill bestämma sannolikheten för att varje färg måste lämna efter ett slumpmässigt urval.

Källa: Pexels

Det är tråkigt att föreställa sig att få ett gummi, spela in det, returnera det, ta ut ett gummi och upprepa samma flera hundra eller flera tusen gånger. Du kan till och med vilja observera beteendet efter flera miljoner iterationer.

Men tvärtom är det intressant att upptäcka att efter få repetitioner är den förväntade sannolikheten för 25% inte fullt ut uppfylld, åtminstone inte för alla färger efter 100 iterationer inträffar.

Enligt frekvenssannolikhetsmetoden kommer tilldelningen av värden endast att ske genom att studera många iterationer. På detta sätt måste processen genomföras och företrädesvis registreras på ett datoriserat eller emulerat sätt.

Flera strömmar avvisar frekvenssannolikhet och argumenterar brist på empirism och tillförlitlighet i slumpmässiga kriterier.

[TOC]

Hur beräknas frekvenssannolikheten?

När du programmerar experimentet i alla gränssnitt som kan erbjuda en rent slumpmässig iteration kan du börja studera frekvenssannolikheten för fenomenet genom en värdentabell.

Det föregående exemplet uppskattas från frekvensmetoden:

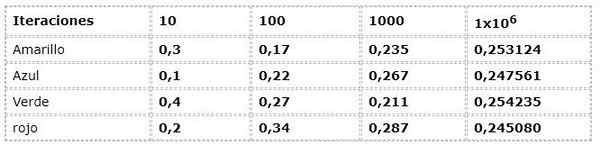
Numeriska data motsvarar uttrycket:

N (a) = antal förekomster/ antal iterationer

Där n (a) representerar den relativa frekvensen för "A" -händelsen

“A” tillhör uppsättningen möjliga resultat eller provutrymme Ω

Det kan tjäna dig: multiplar på 8: Vad är och förklaring

Ω: röd, grön, blå, gul

Det finns en betydande spridning i de första iterationerna, när frekvenser med upp till 30% av skillnaderna observeras med varandra, vilket är ett mycket högt faktum för ett experiment som teoretiskt har händelser med samma möjlighet (utrustning).

Men när iterationerna växer verkar värden mer och mer för de som presenteras av den teoretiska och logiska strömmen.

Lagen om de stora siffrorna

Som ett oväntat avtal mellan de teoretiska och frekvensmetoderna uppstår lagen om stort antal. Där det konstateras att efter en betydande mängd iterationer närmar sig värdena för frekvensexperimentet teoretiska värden.

I exemplet kan du märka hur värden är ungefärliga till 0,250 när iterationer växer. Detta fenomen är elementärt i slutsatserna från många sannolikheter.

Källa: Pexels

Andra sannolikhetsmetoder

Det finns ytterligare två teorier eller tillvägagångssätt för begreppet sannolikhet utöver Frekvenssannolikhet.

Logisk teori

Din strategi är inriktad på fenomenens deduktiva logik. I föregående exempel är sannolikheten för att få varje färg 25% stängd. Med andra ord.

Subjektiv teori

Det är baserat på kunskapen och tidigare övertygelser som varje individ har om fenomen och attribut. Uttalanden som "Det regnar alltid i heliga veckan " De följer ett mönster av liknande händelser som tidigare har inträffat.

Historia

Början av dess implementeringsdatum från 1800 -talet, när jag har citerat det i flera av dess arbete i Cambridge England. Men det var inte förrän det tjugonde århundradet som 2 statistisk matematik utvecklade och formade Frekvenssannolikhet.

Kan tjäna dig: polynomiska ekvationer

En av dem var Hans Reichenbach, som utvecklar sitt arbete i publikationer som "Teori om sannolikhet" som publicerades 1949.

Den andra var Richard Von Mises, som utvecklade sitt arbete mer grundligt genom flera publikationer och föreslog att betrakta sannolikheten som en matematisk vetenskap. Detta koncept var nytt i matematik och skulle markera början på en era av tillväxt i studien av Frekvenssannolikhet.

Egentligen gör denna händelse den enda skillnaden med de bidrag som gjorts av generationen av Venn, Counot och Helm. Där sannolikheten blir en motsvarighet som geometri och mekanik.

< La teoría de las probabilidades trata con massiva fenomen och repetitiva händelser. Problem där antingen samma händelse upprepas om och om igen, eller ett stort antal enhetliga element är involverade samtidigt> Richard Von Mises

Massiva fenomen och repetitiva händelser

Tre typer kan klassificeras:

• Fysik: Obdosmönster av naturen utöver ett slumpmässigt tillstånd. Till exempel beteendet hos molekylerna i ett element i ett prov.
• Chans: Dess grundläggande övervägande är slumpmässighet, som genom att släppa en tärning upprepade gånger.
• Biologisk statistik: Val av testämne enligt deras egenskaper och attribut.

I teorin spelar individen som mäter en roll i sannolikhetsuppgifterna, eftersom det är hans kunskap och erfarenheter som formulerar detta värde eller förutsägelse.

I Frekvenssannolikhet Händelser kommer att betraktas som samlingar som ska behandlas, där individen inte spelar någon roll i uppskattningen.

Attribut

I varje element inträffar ett attribut, vilket kommer att vara varierande beroende på detta. Till exempel i typen av fysiskt fenomen kommer vattenmolekyler att ha olika hastigheter.

Det kan tjäna dig: triangulösa likhetskriterier

I lanseringen av tärningarna känner vi till provutrymmet ω som representerar experimentets attribut.

Ω: 1, 2, 3, 4, 5, 6

Det finns andra attribut som ω_P  eller vara udda Ω_Yo

Ω_p : 2, 4, 6

Ω_Yo : 1, 3, 5

Som kan definieras som icke -elementära attribut.

Exempel

• Du vill beräkna frekvensen för varje möjlig summa vid lanseringen av två tärningar.

För detta programmeras ett experiment där två slumpmässiga värden mellan [1, 6] tillsätts i varje iteration.

Uppgifterna registreras i en tabell och trender i stort antal studeras.

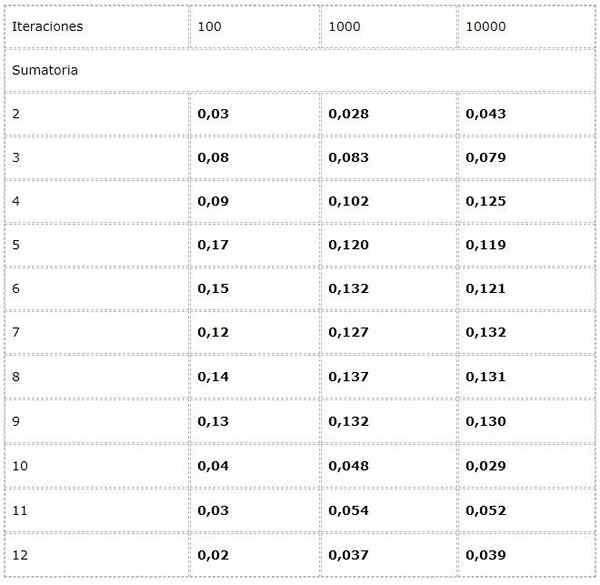
Det observeras att resultaten kan variera avsevärt mellan iterationer. Emellertid kan lagen om stort antal ses i den uppenbara konvergensen som presenteras i de två sista kolumnerna.

Referenser

1. Statistik och utvärdering av bevis för kriminaltekniska forskare. Andra upplagan. Colin g.G. Aitken. Matematikskola. University of Edinburgh, Storbritannien
2. Matematik för datavetenskap. Eric Lehman. Google Inc.
   F Thomson Leighton Department of Mathematics and the Computer Science and AI Laboratory, Massachussetts Institute of Technology; Akamai -teknik
3. Den aritmetiska läraren, volym 29. National Council of Teachers of Mathematics, 1981. Michigan universitet.
4. Lärande och undervisningsnummerteori: Forskning inom kognition och instruktion / redigerad av Stephen R. Campbell och Rina Zazkis. ACTEX Publishing 88 Post Road West, Westport CT 06881
5. Bernoulli, J. (1987). Ars antagande och 4ème partie. Rouen: Irem.