Anmärkningsvärda produkter

Vilka är anmärkningsvärda produkter?

Anmärkningsvärda produkter är algebraiska operationer, där multiplikationer av polynom uttrycks, som inte behöver traditionellt lösas, men med hjälp av vissa regler kan resultaten av samma hittas hittas.

Polynom multipliceras med om det därför är möjligt att de har många termer och variabler. För att göra processen kort används reglerna för de anmärkningsvärda produkterna, som tillåter multiplikationer utan att behöva gå för termin.

Anmärkningsvärda produkter och exempel

Varje anmärkningsvärd produkt är en formel som är resultatet av en faktorisering, sammansatt av polynom i flera termer som binomialer eller trinomialer, kallade faktorer.

Faktorerna är grunden för en makt och har en exponent. När faktorerna multipliceras måste exponenterna läggas till.

Det finns flera anmärkningsvärda produktformler, vissa används mer än andra, beroende på polynomer och är följande:

Fyrkantig binomial

Det är multiplikationen av ett binomial av sig själv, uttryckt i form av makt, där termerna läggs till eller subtraheras:

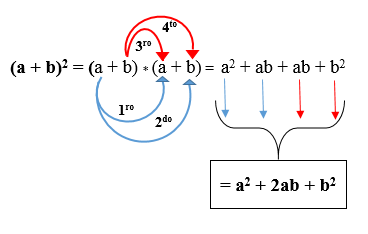
till. Fyrkantig summa binomial: Det är lika med kvadratet för den första terminen, plus dubbelt så mycket som termerna, plus kvadratet för den andra terminen. Det uttrycks enligt följande:

(A + B)² = (a + b) _* (A + B).

I följande figur kan du se hur produkten utvecklas enligt den ovannämnda regeln. Resultatet kallas trinomial av ett perfekt torg.

Exempel 1

(x + 5) ² = x² + 2 (x * 5) + 5²

(x + 5) ² = x² + 2 (5x) + 25

(x + 5) ² = x² + 10x + 25.

Exempel 2

(4a + 2b) = (4a)² + 2 (4: e _* 2b) + (2b)²

(4a + 2b) = 8a² + 2 (8ab) + 4b²

(4a + 2b) = 8a² + 16 AB + 4B².

b. Binomial av en fyrkantig subtraktion: Samma regel i binomialen för en summa tillämpas, bara den i detta fall den andra termen är negativ. Dess formel är som följer:

(A - B)² = [(a) + (- b)]²

Kan tjäna dig: Numeriska analogier: Typer, applikationer och övningar

(A - B)² = a² +2: a _* (-b) + (-b)²

(A - B)²   = a² - 2AB + B².

Exempel 1

(2x - 6)² = (2x)² - 2 (2x _* 6) + 6²

(2x - 6)²  = 4x² - 2 (12x) + 36

(2x - 6)² = 4x² - 24x + 36.

Konjugat binomials produkt

Två binomialer konjugeras när de andra termerna för var och en är av olika tecken, det vill säga den första är positiv och den andra negativa eller vice versa. Det löses genom att höja varje monomialt kvadrat och subtraheras. Dess formel är som följer:

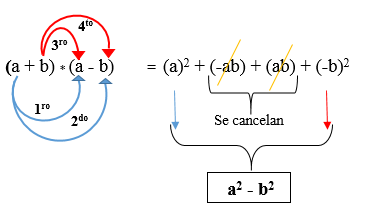
(A + B) _* (A - B)

I följande figur utvecklas produkten av två konjugerade binomialer, där det observeras att resultatet är en skillnad i rutor.

Exempel 1

(2a + 3b) (2a - 3b) = 4a² + (-6AB) + (6 AB) + (-9b²)

(2a + 3b) (2a - 3b) = 4a² - 9b².

Produkt av två binomialer med en gemensam term

Det är en av de mest komplexa och lite använda anmärkningsvärda produkterna eftersom det är en multiplikation av två binomialer som har en gemensam term. Regeln indikerar följande:

• Torget för den gemensamma termen.
• Plus summan villkoren som inte är vanliga och sedan multiplicera dem med den vanliga termen.
• Plus summan av multiplikationen av termerna som inte är vanliga.

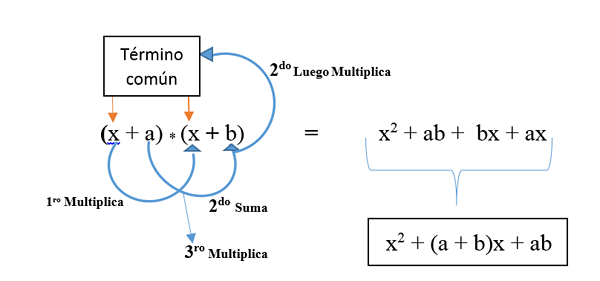
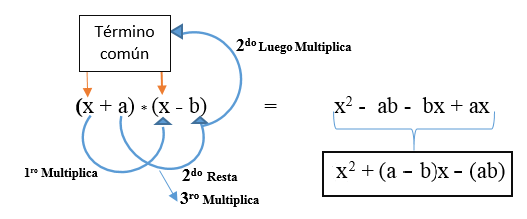
Det representeras i formeln: (x + a) _* (x + b) och utvecklas som visas på bilden. Resultatet är en icke -perfekt fyrkantig trinomial.

Exempel 1

(x + 6) _* (x + 9) = x² + (6 + 9) _* X + (6 _* 9)

(x + 6) _* (x + 9) = x² + 15x + 54.

Det finns möjligheten att den andra termen (den olika termen) är negativ och dess formel är som följer: (x + a) _* (x - b).

Exempel 2

(7x + 4) _* (7x - 2) = (7x _* 7x) + (4 - 2)_* 7x + (4 _* -2)

(7x + 4) _* (7x - 2) = 49x² + (2)_* 7x - 8

(7x + 4) _* (7x - 2) = 49x² + 14x - 8.

Det kan också vara så att båda olika termer är negativa. Din formel kommer att vara: (x - a) _* (x - b).

Kan tjäna dig: Lamy Theorem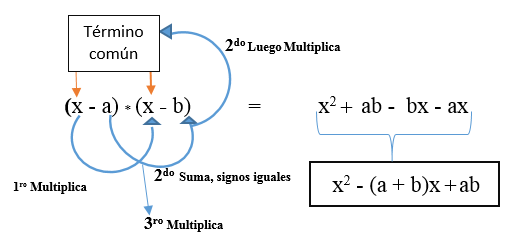

Exempel 3

(3B - 6) _* (3B - 5) = (3B _* 3B) + (-6 - 5)_* (3B) + (-6 _* -5)

(3B - 6) _* (3b - 5) = 9b² + (-elva) _* (3B) + (30)

(3B - 6) _* (3b - 5) = 9b² - 33b + 30.

Fyrkantig polynom

I det här fallet finns det mer än två termer och för att utveckla den, var och en skärs och läggs till med två gånger multiplikationen av en term med en annan; Dess formel är: (a + b + c)² Och resultatet av operationen är en trinomial kvadrat.

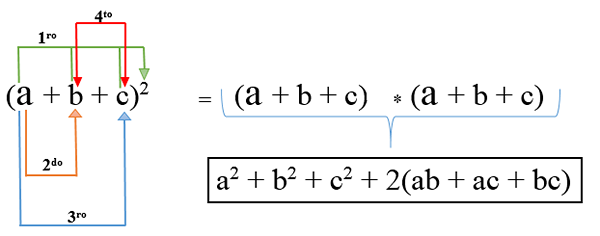
Exempel 1

(3x + 2y + 4z)² = (3x)² + (2 och)² + (4Z)² + 2 (6xy + 12xz + 8yz)

(3x + 2y + 4z)² = 9x² + 4y² + 16Z² + 12xy + 24xz + 16yz.

Kub binomial

Det är en komplex anmärkningsvärd produkt. För att utveckla det multipliceras binomialen med sitt fyrkant, enligt följande:

till. För binomial till kuben av en summa:

• Den första terminen kub, plus trippel torget för den första terminen av den andra.
• Plus tredubbla den första terminen, av den andra kvadrat.
• Plus kuben för den andra terminen.

(A + B)³ = (a + b) _* (A + B)²

(A + B)³ = (a + b) _* (till² + 2AB + B²)

(A + B)³ = a³ + 2: a²B + ab² + ba² + 2AB² + b³

(A + B)³ = a³ + 3: e²B + 3AB² + b³.

Exempel 1

(A + 3)³ = a³ + 3 (a)²_*(3) + 3 (a)_*(3)² + (3)³

(A + 3)³ = a³ + 3 (a)²_*(3) + 3 (a)_*(9) + 27

(A + 3)³ = a³ + 9 a² + 27a + 27.

b. För binomial till kuben för en subtraktion:

• Kuben för den första terminen, utom trippeln på kvadratet för den första terminen av den andra.
• Plus tredubbla den första terminen, av den andra kvadrat.
• Mindre kuben för den andra terminen.

(A - B)³ = (a - b) _* (A - B)²

(A - B)³ = (a - b) _* (till² - 2AB + B²)

(A - B)³ = a³ - 2: a²B + ab² - ba² + 2AB² - b³

(A - B)³ = till³ - 3: e²B + 3AB² - b³.

Exempel 2

(B - 5)³ = B³ + 3 (b)²_*(-5) + 3 (b)_*(-5)² + (-5)³

(B - 5)³ = B³ + 3 (b)²_*(-5) + 3 (b)_*(25) -125

Kan tjäna dig: icke -grupperade data: exempel och träning löst

(B - 5)³ = B³ - 15b² +75b - 125.

Trinomial kub

Den utvecklar multiplicerar det med sitt fyrkant. Det är en mycket omfattande anmärkningsvärd produkt eftersom det finns tre termer som tas upp till kuben, plus trippeln för varje kvadratrödig termin, multiplicerad med var och en av termerna, plus sex gånger produkten av de tre termerna. Sett i en bättre form:

(A + B + C)³ = (A + B + C) _* (A + B + C)²

(A + B + C)³ = (A + B + C) _* (till² + b² + c² + 2AB + 2AC + 2BC)

(A + B + C)³ = A³ + b³ + c³ + 3: e²B + 3AB² + 3: e²C + 3ac² + 3B²C + 3BC² + 6ABC.

Exempel 1

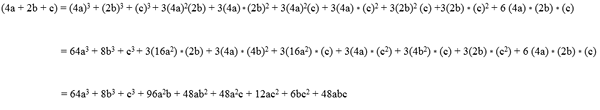
Löst övningar av anmärkningsvärda produkter

Övning 1

Utveckla följande binomial till kuben: (4x - 6)³.

Lösning

Kom ihåg att en binomial till kuben är lika med den första termen som tas upp till kuben, utom trippeln på kvadratet för den första termen av den andra; plus tredubbla den första terminen, vid den andra kvadrat, utom kuben för den andra terminen.

(4x - 6)³ = (4x)³ - 3 (4x)²(6) + 3 (4x) _* (6)² - (6)²

(4x - 6)³ = 64x³ - 3 (16x²) (6) + 3 (4x)_* (36) - 36

(4x - 6)³ = 64x³ - 288x² + 432x - 36.

Övning 2

Utveckla följande binomial: (x + 3) (x + 8).

Lösning

Du har ett binomial där det finns en gemensam term, som är x och den andra termen är positiv. För att utveckla det måste bara den gemensamma termen ökas, plus summan av termerna som inte är vanliga (3 och 8) och sedan multiplicera dem med den gemensamma termen, plus summan av multiplikationen av termerna som inte är vanliga.

(x + 3) (x + 8) = x² + (3 + 8) X + (3_*8)

(x + 3) (x + 8) = x² + 11x + 24.

Referenser

1. Ängel, a. R. (2007). Elementär algebra. Pearson Education,.
2. Arthur Goodman, L. H. (nitton nittiosex). Algebra och trigonometri med analytisk geometri. Pearson Education.
3. Das, s. (s.F.). Matematik plus 8. Storbritannien: Sagar Ratna.
4. Jerome e. Kaufmann, k. L. (2011). Elementär och mellanliggande algebra: En kombinerad strategi. Florida: Cengage Learning.
5. Pérez, c. D. (2010). Pearson Education.